基于油缸压力的液压支架姿态及受载反演
周 凯,任怀伟,华宏星,郑 辉
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.天地科技股份有限公司 开采设计事业部,北京 100013)
基于油缸压力的液压支架姿态及受载反演
周 凯1,任怀伟2,华宏星1,郑 辉1
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.天地科技股份有限公司 开采设计事业部,北京 100013)
液压支架的位姿、受载信息的感知是其自适应控制的基础。通过建立液压支架的矢量闭环运动方程和分别对顶梁、掩护梁进行受力分析,给出了立柱、平衡千斤顶油压与支架位姿参数和顶梁载荷之间的数学关系,从而建立了基于油缸压力的液压支架姿态及受载信息反演的数学模型。以ZY12000/28/64支顶掩护式液压支架为对象,通过ADAMS模型与本文数学模型的计算结果对比,验证了该数学模型的有效性和准确性。该模型将为液压支架的自适应控制提供技术支撑。
油缸压力;液压支架;姿态;受载;反演;矢量闭环
较浅部开采而言,深部开采面临更加复杂及危险的环境,因此亟需实现无人化采掘来提高采掘作业的安全性和高效性。液压支架作为深部煤层采掘装备的重要组成部分,它能否及时适应围岩及底板的应力及位置变化并作出相应的调整,关系到支护系统的结构安全性和支护稳定性[1-2]。而为了实现液压支架的姿态自适应调控,需掌握其姿态信息及受载信息。直接测量这些信息需布置大量倾角传感器,而这些传感器在复杂采场下的维护也是个难题。因此,基于液压支架易测得的有限信息来反演其姿态和受载成了液压支架自适应控制领域研究热点之一。
为了得到液压支架立柱千斤顶、平衡千斤顶的油压与煤岩作用在顶梁上的合力大小和位置间的关系,樊军等人[3-12]将顶梁和掩护梁分别作为隔离体,根据力和力矩平衡原理,确定了立柱、平衡千斤顶的受力与顶梁合力大小及位置的关系。这些研究多以液压支架在水平位置处进行受力分析,与液压支架的顶梁并非总是处于水平位置的实际工况有一定的偏差;Vaze等人[13]建立了支架前连杆倾角和顶梁俯仰角与立柱伸缩长度之间的数学关系,从而进一步确定支架的位姿参数;Ferreras等人[14]建立液压支架ADAMS模型,通过改变立柱油缸的速度,得到各部件的质心速度,从而分析了支架上升过程中各部件之间的运动学关系;朱殿瑞[15]通过倾角传感器测出底座、前连杆及顶梁与水平面的夹角,再进一步建立支架处于某一姿态下的运动方程,从而建立了相应的支架姿态监测理论;文治国[16]首先根据支架顶梁、底座、后连杆与水平面的倾角确定了液压支架的姿态参数,并以此为基础,对两柱掩护式的液压支架在该姿态下进行了顶梁和掩护梁的受力分析,并提出了相应的姿态自适应控制策略;白雪峰[17]在通过传感器测定前连杆倾角和平衡千斤顶工作长度的基础上,进一步计算支架的全部运动参数,再根据该姿态下立柱千斤顶和平衡千斤顶的油压值,计算出了支架的受载信息。
这些学者的研究表明,欲确定支架顶梁上的载荷,需要掌握液压支架立柱千斤顶和平衡千斤顶的油压及各部件的姿态信息,而获得液压支架尺寸参数及油压是确定液压支架的姿态信息的前提条件。
本文以两柱掩护式液压支架为研究对象,基于建立的立柱、平衡千斤顶油缸油压与支架姿态及受载的数学关系,提出了利用立柱、平衡油缸压力来反演液压支架姿态、并进一步给出液压支架受载信息的确定方法。从而实现用最少的测量参数确定液压支架的姿态和受载,为液压支架的自适应调控提供技术支撑。
1 理论模型
1.1 液压支架的运动学分析
支顶掩护式液压支架二维运动学模型如图1所示[18],以底座后端作为坐标系原点O,表1列出了图中各物理参数的物理意义。
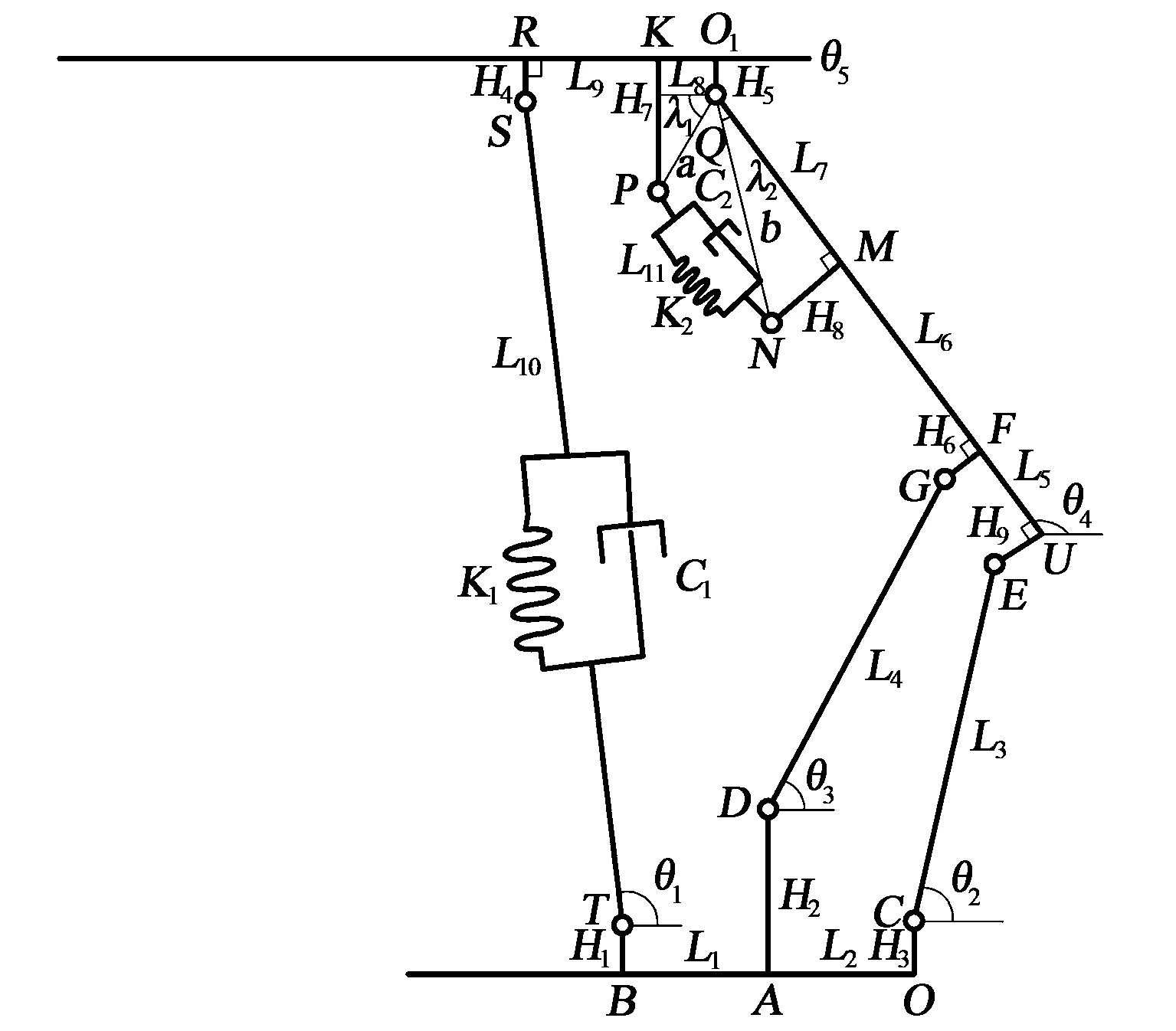
图1 支顶掩护式液压支架运动学模型
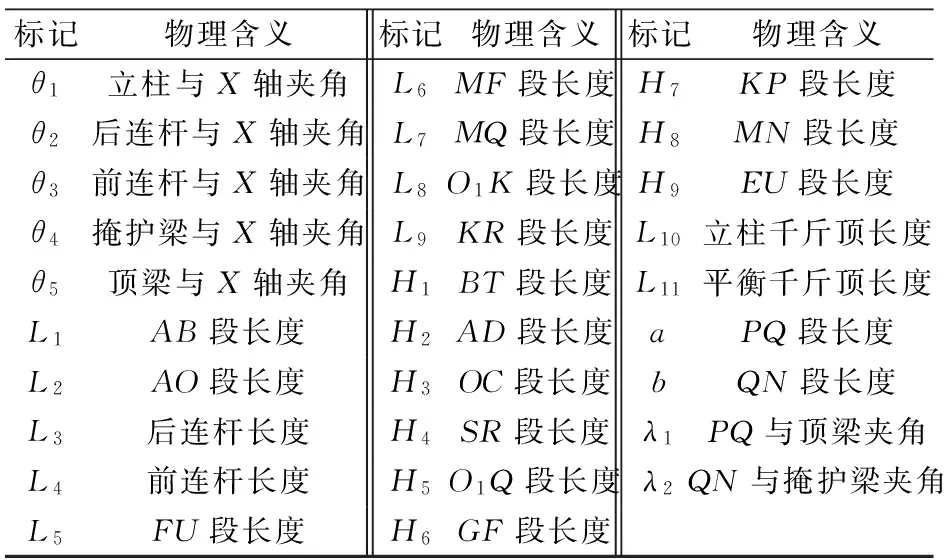
标记物理含义标记物理含义标记物理含义θ1立柱与X轴夹角L6MF段长度H7KP段长度θ2后连杆与X轴夹角L7MQ段长度H8MN段长度θ3前连杆与X轴夹角L8O1K段长度H9EU段长度θ4掩护梁与X轴夹角L9KR段长度L10立柱千斤顶长度θ5顶梁与X轴夹角H1BT段长度L11平衡千斤顶长度L1AB段长度H2AD段长度aPQ段长度L2AO段长度H3OC段长度bQN段长度L3后连杆长度H4SR段长度λ1PQ与顶梁夹角L4前连杆长度H5O1Q段长度λ2QN与掩护梁夹角L5FU段长度H6GF段长度
考虑到液压支架工作时,除液压缸外,其余各部件自身弹性变形很小,故将这些部件视为刚体。根据矢量闭环原理,建立的封闭方程组如下:
(1)
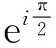
(2)
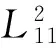
(3)
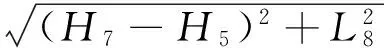
将(1)、(2)、(3)式进行虚部、实部分离,并令各式等号两边实部和虚部分别相等,可得支架的运动学位移关系如下:
-L2+L4cosθ3+H6sinθ4=L3cosθ2+H9sinθ4+L5cosθ4
(4)
H2+L4sinθ3-H6cosθ4=H3+L3sinθ2-H9cosθ4+
L5sinθ4
(5)
-L1+L10cosθ1-H4sinθ5+(L8+L9)cosθ5=L4cosθ3+H6sinθ4+(L6+L7)cosθ4-H5sinθ5
(6)
H1+L10sinθ1+H4cosθ5+(L8+L9)sinθ5=H2+L4sinθ3-H6cosθ4+(L6+L7)sinθ4+H5cosθ5
(7)
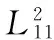
(8)
由立柱油缸和平衡油缸等效刚度K10,K11计算公式[19],可分别计算求得工况下立柱油缸和平衡油缸的长度
L10=L100-(P11-P10)A1/K10
(9)
L11=L110-(P21-P20)A2/K11
(10)
式中,P11和P21分别为立柱油缸压力、平衡油缸压力,可实时测得;L100,L110分别为立柱油缸和平衡油缸的初始长度;P10,P20分别为立柱油缸和平衡油缸的初始压力;A1,A2分别为立柱油缸和平衡油缸的液柱横截面积。
对于一个确定的液压支架,其设计尺寸已知,在此前提下,方程组(4)~(8)中共有7个未知数:θ1,θ2,θ3,θ4,θ5,L10,L11。若由(9)、(10)两式获得L10及L11的数值,则剩余的5个参数可由5个封闭非常组(4)~(8)进行求解。考虑到方程组(4)~(8)为非线性方程组,解析解难以获得,可通过Newton-Raphson法进行求解。这样,就建立了通过油缸压力反推液压支架姿态的数学模型。
1.2 确定姿态参数下的支架受力分析
对支架顶梁进行确定姿态参数条件下的受力分析[20],如图2所示。
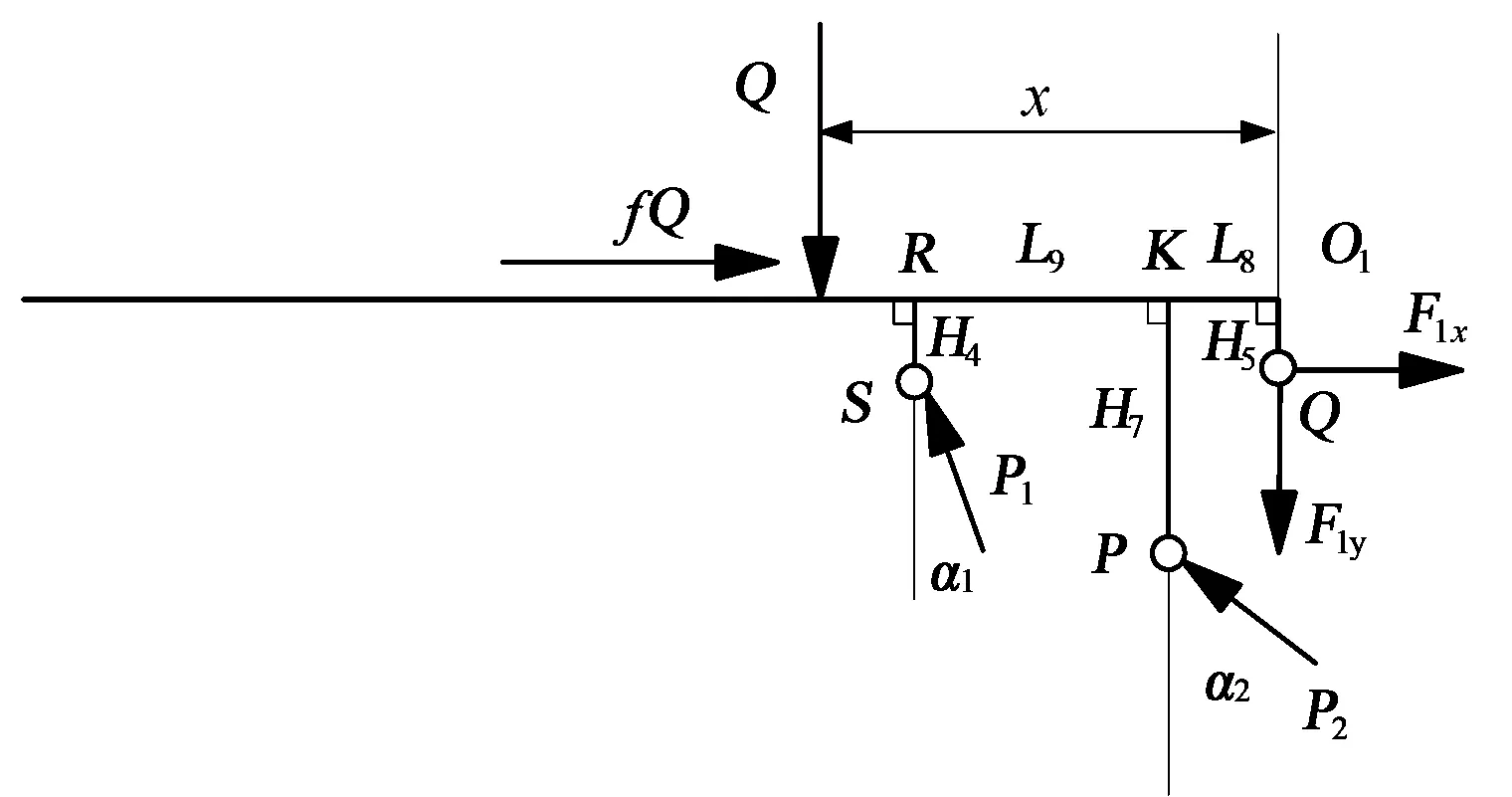
图2 顶梁受力示意
将各力分解到沿顶梁方向及垂直于顶梁的方向上,根据力平衡和关于O1点力矩平衡,可得
F1y+Q=P1cosα1+P2cosα2
(11)
F1x+fQ=P1sinα1+P2sinα2
(12)
Qx+F1x·H5=P1sinα1·H4+P1cosα1·(L8+L9)+P2sinα2·H7+P2cosα2·L8
(13)
其中,F1x,F1y为顶梁与掩护梁铰接点上受力;P1,P2分别是立柱千斤顶和平衡千斤顶的工作阻力(P1=P11A1,P2=P21A2);Q是顶梁载荷的集中力;fQ是顶梁所受的摩擦力;α1,α2分别是立柱千斤顶与RS直线的夹角、平衡千斤顶与KP直线的夹角,分别由以下几何关系求得:

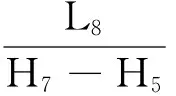
∠PQN=θ4-θ5-λ1-λ2
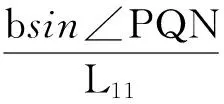
类似地对图3所示的掩护梁进行受力分析[20]。将各力分解到沿掩护梁方向及垂直于掩护梁的方向上,根据力平衡和关于U点力矩平衡,可得
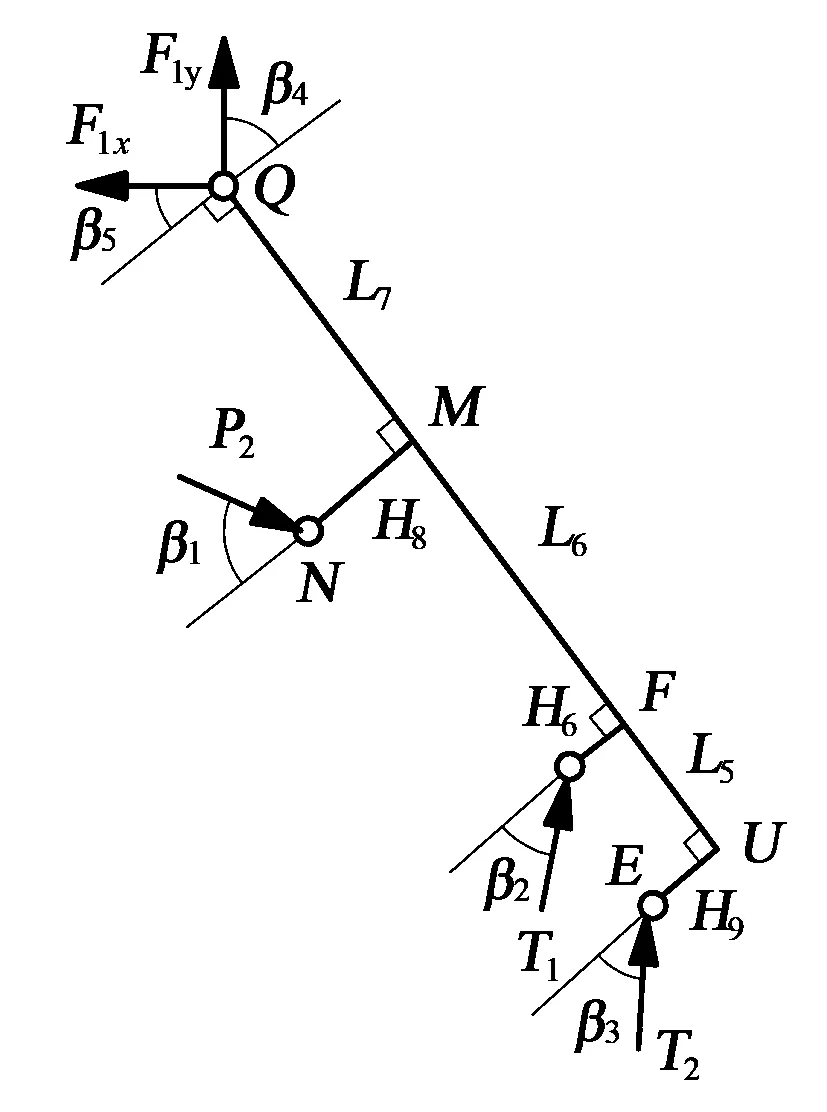
图3 掩护梁受力示意
F1xcosβ5=F1ycosβ4+P2cosβ1+T1cosβ2+T2cosβ3
(14)
P2sinβ1=F1xsinβ5+F1ysinβ4+T1sinβ2+T2sinβ3
(15)
F1xcosβ5·(L5+L6+L7)+P2sinβ1·H8=P2cosβ1·(L5+L6)+T1sinβ2·H6+T1cosβ2·L5+T2sinβ3·H9+F1ycosβ4·(L5+L6+L7)
(16)
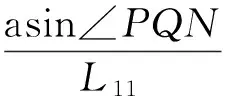
解得顶梁力载幅值Q和合力作用点位置x分别为:
Q=(P1sinα1·Q1+P2sinα2·Q1-P1cosα1·Q2-
P2cosα2·Q2+P2Q3)/(fQ1-Q2)
(17)
x=fH5+[P1sinα1·H4+P1cosα1·(L8+L9)+
P2sinα2·H7+P2cosα2·L8-P1sinα1·H5-
P2sinα2·H5]·(fQ1-Q2)/(P1sinα1·Q1+
P2sinα2·Q1-P1cosα1·Q2-P2cosα2·Q2+P2Q3)
(18)
式中,P1=P10A10
P2=P11A11
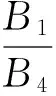
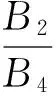
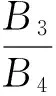
K1=cosβ5·(L5+L6+L7)
K2=sinβ1H8-cosβ1·(L5+L6)
K3=sinβ2H6+cosβ2·L5
K4=sinβ3·H9
K5=cosβ4·(L5+L6+L7)
A1=sinβ2cosβ5+sinβ5cosβ2
A2=sinβ4cosβ2-sinβ2cosβ4
A3=sinβ2cosβ1+sinβ1cosβ2
A4=sinβ2cosβ3-sinβ3cosβ2
B1=sinβ3cosβ5+sinβ5cosβ3
B2=sinβ4cosβ3-sinβ3cosβ4
B3=sinβ3cosβ1+sinβ1cosβ3
B4=sinβ3cosβ2-sinβ2cosβ3
式(17)和(18)分别给出了两液压缸压力和顶梁受载合力大小、位置的数学关系。基于该数学关系,便可由液压缸的压力反推作用于顶梁上的合力大小和合力作用点位置。
图4为反演流程图。首先把可通过测量获取的立柱、平衡油缸的压力P11,P21代入建立的矢量闭环运动学方程,经Newton-Raphson迭代求得液压支架的工作姿态参数θ1,θ2,θ3,θ4,θ5,再进行该姿态下顶梁及掩护梁的受力分析,应用建立的油缸压力P11,P21和顶梁作用力合力大小及作用点f,x间的数学关系,实现由立柱、平衡油缸压力反演液压支架工作姿态和顶梁合力大小及合力作用位置。
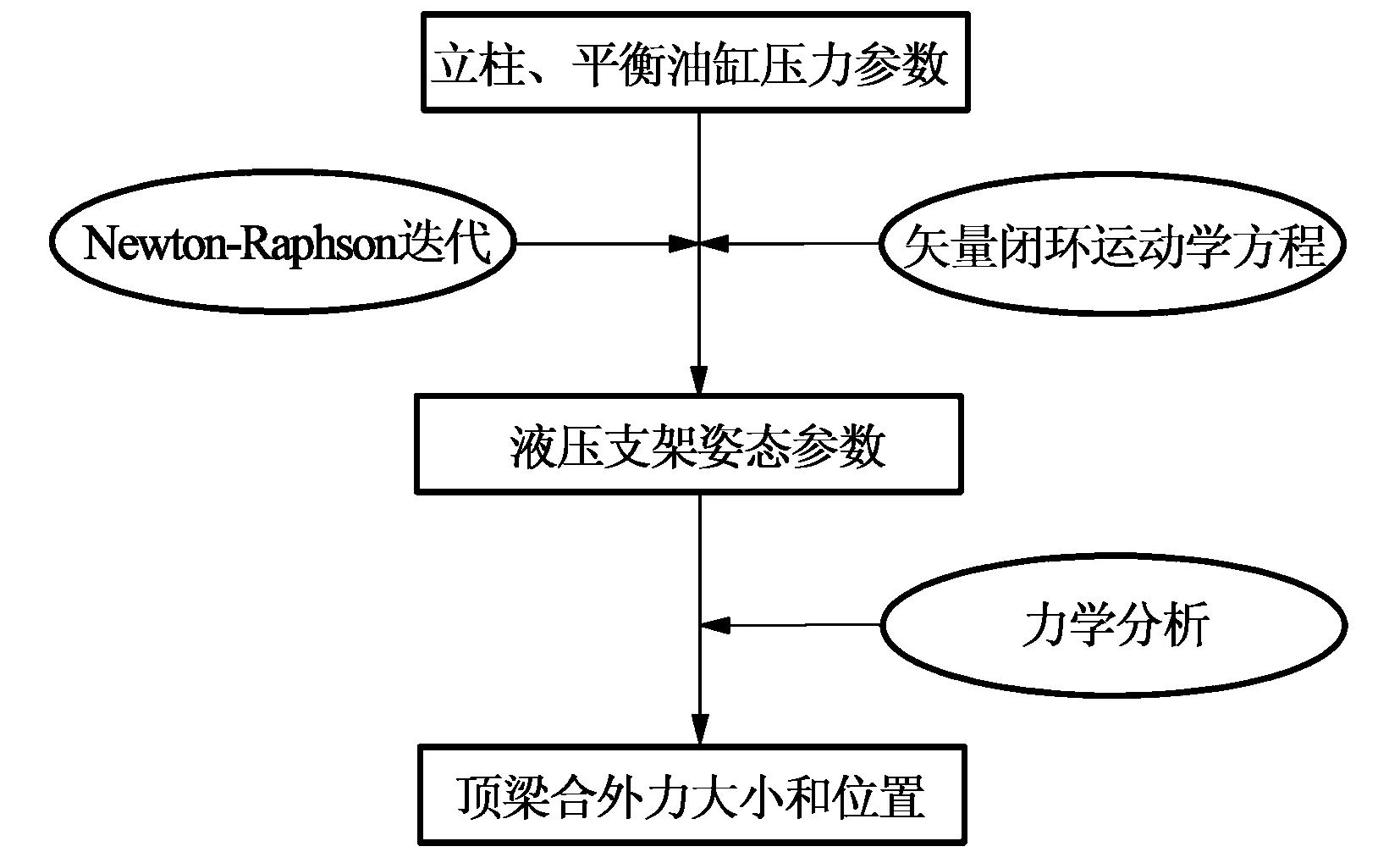
图4 液压支架姿态、受载反演流程
该方法用于液压支架运动学及受力分析仅需测量立柱、平衡千斤顶的油压,避免了为支架的运动学分析需布置传感器获得部分部件的运动学参数信息环节[16-17],从而实现了用较易测得的已知参数获取液压支架的姿态及受载信息的目标。
2 数值仿真验证
为验证上节数学模型的正确性和有效性,以ZY12000/28/64型液压支架为对象。在SolidWorks中建立其三维模型,并将虚拟样机导入到ADAMS中。用弹簧模拟液压缸,其刚度值由等效刚度[19]确定,建立相应的静力学仿真模型如图5所示。
对ADAMS模型中液压支架的顶梁加集中力,通过静力分析模块计算得到各部件的姿态参数运动量Δθ1,Δθ2,Δθ3,Δθ4,Δθ5(ADAMS正向计算结果);同时提取立柱油缸和平衡油缸的变形量,代入到数学模型(式(9,10,17,18))中,求得液压支架姿态参数运动量Δθ1,Δθ2,Δθ3,Δθ4,Δθ5、合力大小Q和合力作用位置参数x(反演结果)。比较数值仿真结果和数学反演结果,以验证反演方法的有效性。

图5 支架的ADAMS静力学分析模型
由于工程实际中平均合力作用点位置基本上在顶梁立柱铰接点的前后150~300mm的范围内[20],故验证在该力平衡区内进行,共反演计算了3个作用力大小及3个作用点位置共9个工况的姿态及合力参数。具体的ADAMS数值计算结果和基于本文的反演方法得到的结果在表2中列出。定义误差公式e=反演值-ADAMS值/ADAMS值×100%,则反演的合力大小和位置的误差如图6所示,横坐标为工况编号,纵坐标为误差。
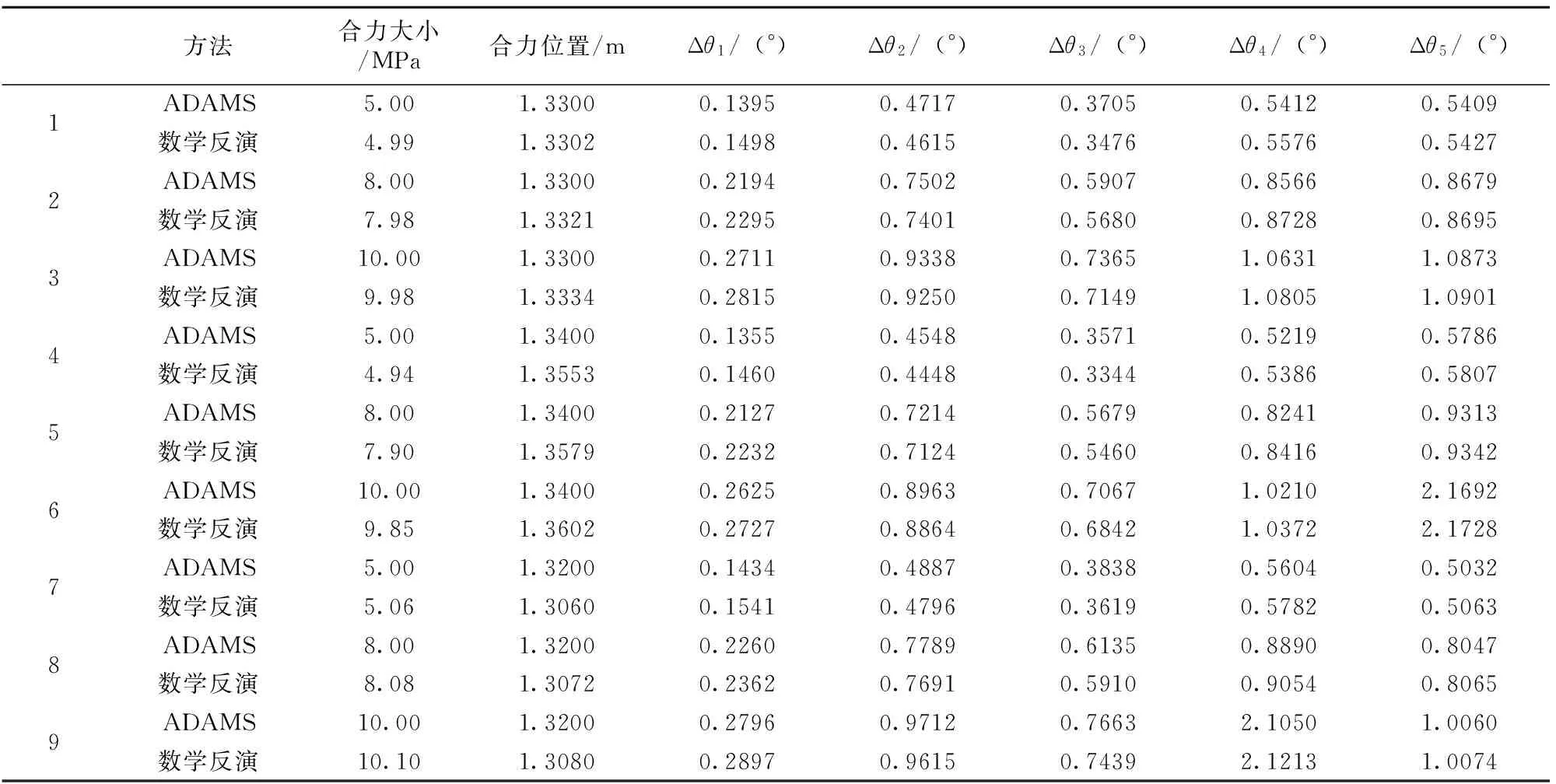
表2 姿态参数、合力参数的ADAMS计算结果与基于数学模型的反演结果比较
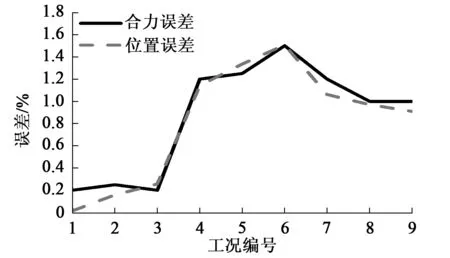
图6 反演的合力大小及位置误差
由表2所列结果可知,基于液压缸压力反演液压支架的姿态参数和合力大小、作用点位置参数与数值仿真结果基本吻合,合力大小最大误差为1.5%,证明了提出的基于液压缸压力反演支架姿态及受载信息方法的可靠性。
3 结 论
以支顶掩护式液压支架为研究对象,应用矢量闭环原理,给出了描述支架各部件质心的运动学方程组,并通过确定姿态下的顶梁和掩护梁受力分析,建立了立柱油缸压力和平衡油缸压力与液压支架姿态和作用于顶梁上合力大小及作用位置的数学关系。据此提出了基于液压缸压力反演支架姿态及受载信息的方法。分别进行顶梁受载的ADAMS正向仿真计算和基于从ADAMS计算结果中提取的液压缸压力反演计算支架的位姿、顶梁合力,通过对比正向计算结果和反演结果,证明了该反演方法的可靠性。
[1]王金华.我国大采高综采技术与装备的现状及发展趋势[J].煤炭科学技术,2006,34(1):4-7.
[2]张银亮,赵 军.国产大采高液压支架的研究现状与发展趋势[J].煤矿开采,2008,13(6):1- 3.
[3]樊 军,钱玉军,徐祖辉.两柱掩护式液压支架受力分析及结构件强度校核[J].煤矿机电,2008(2):111-112.
[4]李厚常.液压支架的力学分析[J].煤矿机械,2009,30(7):69-71.
[5]马希青,鲍森茂,李艳娇.液压支架顶梁的力学分析[J].中国电子商务,2013 (24):122-122.
[6]焦 青,王在伟.ZY9000/25/45型掩护式液压支架受力分析[J].煤矿机械,2011,32(5):83-84.
[7]王永军.支撑掩护式液压支架受力分析[J].煤矿开采,2007,12(3):14-15.
[8]王国法.液压支架技术[M].北京:煤炭工业出版社,1999.
[9]马力平.掩护式液压支架平衡千斤顶液压回路分析[D].太原:太原理工大学,2010.
[10]张守柱.支撑掩护式液压支架的受力分析与计算[J].煤炭科学技术,1979(11):6-14.
[11]张 浩.大采高工作面液压支架结构受力分析[D].淮南:安徽理工大学,2014.
[12]姚贵英,杜小勇,李秋生,等.二柱掩护式液压支架受力分析及优化[J].煤矿机械,2013,34(1):100-102.
[13]Vaze J,Jenkins B R,Jin T,et at.Soils fieldwork,analysis,and interpretation to support hydraulic and hydrodynamic modelling in the Murray floodplains.[J].Soil Research,2010,48(4):295-308.
[14]Juárez-Ferreras R,González-Nicieza C,Menéndez-Díaz A,et al.Measurement and analysis of the roof pressure on hydraulic props in longwall[J].International Journal of Coal Geology,2008,75(1):49-62.
[15]朱殿瑞.掩护式液压支架姿态监测的理论与主要部件的有限元分析[D].太原:太原理工大学,2012.
[16]文治国.自动化工作面两柱掩护式液压支架姿态自适应技术研究[D].煤炭科学研究总院,2015.
[17]白雪峰.掩护式支架姿态监测与控制的研究[D].太原:太原理工大学,2006.
[18]周 凯,李明瑞,焦素娟.基于耦合动力学模型的围岩-支架相互作用分析[J].煤炭学报,2015,40(11):2534-2539.
[19]刘欣科,赵忠辉,赵 锐.冲击载荷作用下液压支架立柱动态特性研究[J].煤炭科学技术,2012,40(12):66-70.
[20]钱鸣高.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010.
[责任编辑:徐亚军]
LoadingInversionandHydraulicSupportPoseBasedonCylinderPressure
ZHOU Kai1,REN Huai-wei2,HUA Hong-xing1,ZHENG Hui1
(1.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai 200240,China;2.Coal Mining & Designing Department,Tiandi Science & Technology Co.,Ltd.,Beijing 100013,China)
The perception of hydraulic support pose and loading information was the foundation of self-adaptation control,according closed loop vector movement equation,and mechanics state of roof beam and shield beam were analyzed,then the mathematics relation between column,oil pressure of balance jack,support pose parameters and roof beam loading was put forward,and the mathematics model of hydraulic support pose that based on cylinder pressure and loading information inversion.It taking hydraulic shield support of ZY12000/28/64 as studying objects.According results comparison of ADAMS model and the mathematics model,the effectively and precision were verified by it.The model would proved technical supporting for self adaption control.
cylinder pressure;hydraulic support;pose;loading;inversion;closed loop vector
TD355.41
A
1006-6225(2017)05-0036-05
2017-06-29
10.13532/j.cnki.cn11-3677/td.2017.05.009
国家重点基础研究发展计划(973计划)基金资助项目(2014CB046302)
周 凯(1992-),男,安徽无为人,在读博士。
周 凯,任怀伟,华宏星,等.基于油缸压力的液压支架姿态及受载反演[J].煤矿开采,2017,22(5):36-40.

