基于遗传算法的颚式破碎机优化设计

吴雪峰, 范 玉

(河南理工大学 机械与动力工程学院, 河南 焦作454000)

基于遗传算法的颚式破碎机优化设计

吴雪峰, 范 玉

(河南理工大学 机械与动力工程学院, 河南 焦作454000)

复摆式颚式破碎机的设计参数主要包括整体机构参数、腔形参数及工作参数, 各参数的配置情况直接影响机器生产能力, 因此对颚式破碎机的优化设计尤为必要.以PE 250×400型颚式破碎机作为优化对象, 以提高颚式破碎机生产率作为优化设计目标, 以影响生产率的各构件基本尺寸作为优化设计变量, 建立包含机构参数、腔形参数和工作参数的约束条件, 构建基于遗传算法的颚式破碎机优化设计数学模型.在利用遗传算法完成颚式破碎机初步优化的基础上, 通过人机配合采用3种方案分别进行两次优化, 得到不同方案的优化结果.通过对比分析最终确定了适合PE 250×400型颚式破碎机的优化设计方案, 为颚式破碎机的优化设计提供理论和方法指导.

遗传算法; 优化设计; 颚式破碎机; 生产率

在“十三五”规划纲要中, 明确提出要全面节约和高效利用资源, 要坚持节约优先, 树立“节约、集约、循环利用”的资源观.因此, 有效提高破碎机性能, 降低功耗, 面向高效节能是破碎机的发展趋势.然而据统计, 全国总能耗的11.4%、全国工业能耗的17.5%来自矿业、建材及矿物制品加工等行业, 而各类选矿厂能耗的40%～70%都用于碎磨, 但仅1%～3%总能耗用于磨矿所做的有效功.破碎物料的需要不断增加, 贫矿再利用的比重不断增大, 因此对破碎生产率的改善变得越来越迫切[1-2].

采用传统方法对颚式破碎机的机构尺寸参数进行设计, 无法实现最优结果, 阻碍了颚式破碎机功能的高效发挥.例如, 黄大明等[3]以优化机构平衡质量及其方向角为研究目标, 对PE 600×900型破碎机进行了动力学参数设计, 利用Matlab软件实现了优化计算; 王晓敏等[4]利用ADAMS(automatic dynamic analysis of mechanical systems)软件对PE 600×900型复摆式颚式破碎机进行了破碎腔优化设计; Soni等[5]采用矩阵法对破碎机工作参数进行统计研究, 实现了双辊式破碎机的优化设计; Olaleye[6]从待破碎物料性能入手, 利用统计方法研究了材料属性与破碎机工作能力的关系.

颚式破碎机的设计必须确保机构参数、腔形参数和工作参数的合理配置, 才能使颚式破碎机工作能力达到最优.在评判颚式破碎机设计好坏的众多指标中, 生产率这一关键指标直接决定破碎机的生产能力.颚式破碎机生产率是指在给定料粒度和排料粒度条件下, 单位时间内破碎机处理的物料量.本文以提高破碎机生产率作为设计目标, 建立包含机构参数、腔形参数和工作参数的约束条件, 利用遗传算法对颚式破碎机进行优化设计.

1 颚式破碎机运动学分析

颚式破碎机的动颚下部水平行程Sx直接影响生产率, 该参数取决于机构自身尺寸, 为构建以生产率为目标函数的优化模型, 需利用解析法对颚式破碎机进行运动学分析, 研究构件尺寸对Sx的影响.

颚式破碎机的主体机构如图1所示, 该机构为曲柄摇杆机构.曲柄OA、连杆AB、肘板BC和机架OC长度分别是l1,l2,l3和l4, 动颚下端宽度为l5.

图1 颚式破碎机机构简图Fig.1 Kinematic sketch of jaw crusher

利用解析法对4杆机构进行分析, 以曲柄转动中心为坐标原点, 建立以下2个封闭矢量方程为

(1)

(2)

将式(1)分别向x和y坐标轴投影, 则可得到各杆角位移方程的分量形式为

l1cosφ1+l2cosφ2=l4cosφ4+l3cosφ3
l1sinφ1+l2sinφ2=l4sinφ4+l3sinφ3

(3)

式中:φ1、φ2、φ3及φ4分别是1、2、3和4等构件相对于x轴的角位移.

将式(2)分别向x和y坐标轴投影, 则可得到动颚齿板D点运动轨迹坐标为

Dx=l4cosφ4+l3cosφ3+l5sinφ3
Dy=l4sinφ4+l3sinφ3+l5cosφ3

(4)

利用式(3)和(4)的求解结果, 可计算出D点两极限位置横坐标之差, 即动颚下部水平行程Sx为

Sx=Dx1-Dx2

(5)

为满足4杆机构力学性能, 要求颚式破碎机机构在运动过程中其最小传动角大于40°或50°[7].由曲柄摇杆机构性质可知, 当曲柄与机架两次共线时, 机构可能会出现最小传动角.若两共线位置传动角分别为γ1和γ2, 取其中最小值为最小传动角γmin.

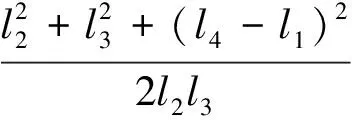
(6)

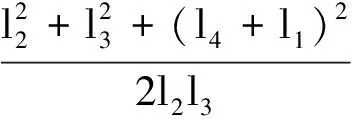
(7)

2 颚式破碎机优化设计模型

2.1目标函数Q

颚式破碎机生产率以动颚摆动一次, 从破碎腔中排出一个松散的棱柱形体积的矿石作为计算依据.根据机构简图, 可计算出单位时间内破碎机排出的棱柱体体积[8]为

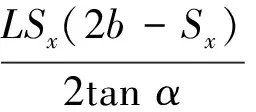
(8)

式中:L为破碎腔长度;b为排矿口宽度;α为啮角.

若已知主轴转速为n, 生产率Q计算式为

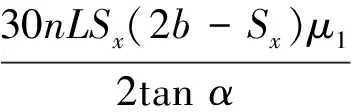
(9)

式中:μ1为压缩破碎棱柱体的填充度.

2.2设计变量X

影响颚式破碎机结构尺寸的主要独立参数有: 曲柄l1、连杆l2、肘板长度l3、两固定铰链距离l4、动颚下端宽度l5, 则设计变量X为

X=[l1,l2,l3,l4,l5]

2.3约束条件

在颚式破碎机生产率的优化方案中, 参数约束条件取值范围选择将直接影响优化结果, 可采用经验类比方法, 确定各约束的取值区间.各约束条件定义如下所示：

(1) 各构件尺寸约束为

9 mm≤l1≤10 mm;
580 mm≤l2≤715 mm;
200 mm≤l3≤300 mm;
475 mm≤l4≤610 mm;
290 mm≤l5≤312 mm.

(10)

(2)颚式破碎机的曲柄与肘板相比较于连杆和机架的长度小得多, 4杆机构存在曲柄的约束条件可简化为

l1+l2≤l3+l4

(11)

l1+l4≤l3+l2

(12)

(3)为实现机构力学性能良好, 确定最小传动角约束条件为

45°≤γmin≤55°

(4)啮角为

14°≤α≤20°

(5)动颚下部水平行程Sx为

12 mm≤Sx≤17 mm

2.4优化模型

利用目标函数及约束条件, 建立变量为5维且具有18个不等式约束的颚式破碎机非线性优化设计模型为

(13)

2.5优化方法

遗传算法是一种全局优化搜索算法, 从任一初始种群出发, 通过随机选择、交叉及变异等操作, 采用概率化的寻优方法产生更适应约束条件的子代, 使群体进化至目标空间中越来越好的区域[9-11].通过若干代的进化, 最后收敛到一群最适合环境的个体, 求得问题的最优解.利用遗传算法对颚式破碎机优化模型计算过程如图2所示.

图2 基于遗传算法的颚式破碎机优化流程图Fig.2 Flow chart of optimization process for jaw crusher based on genetic algorithm

为比较不同方法得到的动颚下端水平行程值以及不同约束条件处理方式对目标函数的影响, 通过人机配合的方式分别按照以下4种条件组合出3种方案进行对比.

条件A: 按理论计算式(5)计算Sx值;

条件B: 按经验计算式计算Sx值为

Sx=8+0.214×bmin

式中: 对于PE 250×400型号破碎机bmin取值为20 mm;

条件C: 采用惩罚函数内点法进行约束条件处理;

条件D: 采用弃除不可行个体法实现约束处理.

方案1与方案2都利用条件D作为约束处理方式, 不同之处在于分别采用条件A和条件B来求解Sx值.

方案1与方案3都采用条件A计算Sx值, 不同之处在于分别采用条件D和条件C作为约束条件处理方式.

3种方案优化结果对比如表1所示.

表1 3种方案优化结果Table 1 Results of the three optimization schemes

3 结果分析

由表1的优化结果可知, 方案2相比方案1计算得到Sx值更大, 但同时啮角也更大, 最终导致目标值较低.显然理论计算法所得结果要优于经验计算法, 因此采用理论计算式来计算Sx值更适合颚式破碎机优化设计.

对比表中方案1和方案3的优化结果, 显然方案3得到的目标值大于方案1.由于方案1采用弃除不可行个体法处理约束条件, 导致种群数目递减, 目标值有所下降.因此，实现约束处理时, 采用惩罚函数内点法要优于弃除不可行个体法.

经过以上分析可知, 方案3可实现目标值最大, 同时动颚水平行程与啮角的参数匹配也优于其他两种方案, 因此选定方案3作为最优设计方案.

方案3优化结果如图3所示, 在优化过程中, 算法迭代到第20代时目标最优解已经收敛到最大值, 为8.34 m3/h.

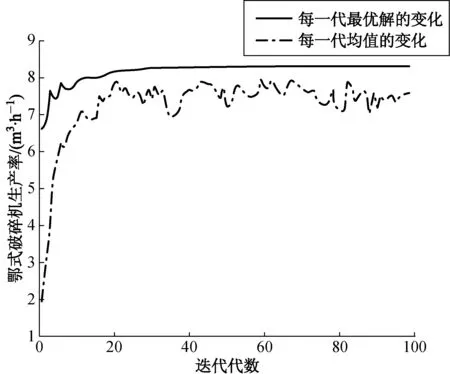
图3 方案3的优化结果Fig.3 Optimization results of the 3rd scheme

4 结 语

本文在利用解析法对颚式破碎机进行运动学分析基础上, 构建基于遗传算法的破碎机优化模型, 分析了不同方法计算动颚下端水平行程Sx对目标函数的影响.结果表明，经验计算式计算出的Sx值大于理论值, 导致啮角随之增大, 目标值降低.同时对遗传算法中不同约束条件处理方式进行对比, 结果表明，惩罚函数内点法要优于采用弃除不可行个体法.最终确定出方案3为最优颚式破碎机设计方案, 即理论计算Sx值与惩罚函数内点法相结合方法可实现生产率函数的最大化, 同时达到主要参数匹配最优, 满足PE 250×400型颚式破碎机优化要求.

[1] 孙康, 李良, 陈俊杰, 等.PE 250×400型复摆颚式破碎机动颚静力学分析[J].机械设计与制造, 2013(5): 102-104．

[2] 蒋飞, 李吉宗, 黄炜斌.PEF 500×750复摆式破碎机的优化设计[J].中国工程机械学报, 2013, 11(6): 512-516．

[3] 黄大明, 杨春兰， 蒋顺梅.基于MATLAB的破碎机动力学参数优化设计[J].机械设计与制造, 2012(3): 28-30.

[4] 王晓敏, 张高青, 孟彩茹.基于Matlab的 PE 600×900复摆颚式破碎机破碎腔优化设计[J].科技创新与应用, 2016(7): 38-39.

[5] SONI S K, SHUKLA S C， KUNDU G. Modeling of particle breakage in a smooth double roll crusher[J].International Journal of Mineral Processing, 2009, 90(1): 97-100.

[6] OLALEYE B. Influence of some rock strength properties on jaw crusher performance in granite quarry[J].Mining Science and Technology (China), 2010, 20(2): 204-208.

[7] 孙桓, 陈作模.机械原理[M].8版.北京: 高等教育出版社, 2013: 43-49.

[8] 郭年琴, 郭晟.颚式破碎机现代设计方法[M].北京: 冶金工业出版社, 2012: 34-39.

[9] 陈国良, 王煦法, 庄镇全, 等, 遗传算法及其应用[M].北京: 人民邮电出版社, 1996: 69-74.

[10] 刘菊蓉, 王旭飞.偏置式曲柄滑块机构的优化设计及运动分析[J].机械研究与应用, 2005,18(6): 99-100．

[11] 雷英杰, 张善文, 李续武, 等.MATLAB遗传算法工具箱及应用[M].西安: 西安电子科技大学出版社, 2005: 95-105.

(责任编辑:杨静)

OptimizationDesignforJawCrusherBasedonGeneticAlgorithm

WUXuefeng,FANYu

(School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454000, China)

Parameters of compound pendulum model jaw crusher contain mechanism dimension, cavity size and working parameters. A reasonable configuration of three parameters impacts production capacity directly, so it is very important to realize the optimization design of jaw crusher. For improving production capacity of jaw crusher, PE 250×400 model jaw crusher is selected as the optimization object. A design parameter optimization model with high production capacity as objectives is established based on genetic algorithm, in which component size of jaw crusher are considered as variables, and the constraint conditions are established, including mechanism dimension, cavity size and working parameters. On the basis of preliminary optimization with genetic algorithm, the second optimization is completed by man-machine cooperation with three schemes, and the optimization results of three schemes are obtained. The optimum solution is determined through analysis of evaluating three schemes. The result offers theoretical basis and guidance for optimization design of jaw crusher.

genetic algorithm; optimal design; jaw crusher; productivity

TH 11

A

1671-0444 (2017)04-0571-04

2017-01-18

河南省高等学校重点科研资助项目(16A416003)

吴雪峰(1980—)，男，吉林吉林人，讲师，博士，研究方向为机械优化设计.E-mail: wuxuefeng@hpu.edu.cn