基于块相关框架的多参考微扰理论和多参考耦合簇理论

邹竞祥 沈 军 许恩华 方 涛 黎书华,*

(1南京大学化学化工学院，介观化学教育部重点实验室，理论与计算化学研究所，南京 210023；2Department of Chemistry,Michigan State University, East Lansing, Michigan 48824, United States；3Graduate School of System Informatics,Kobe University, Kobe, Hyogo 657-0025, Japan)

基于块相关框架的多参考微扰理论和多参考耦合簇理论

邹竞祥1沈 军2许恩华3方 涛1黎书华1,*

(1南京大学化学化工学院，介观化学教育部重点实验室，理论与计算化学研究所，南京 210023；2Department of Chemistry,Michigan State University, East Lansing, Michigan 48824, United States；3Graduate School of System Informatics,Kobe University, Kobe, Hyogo 657-0025, Japan)

传统单参考电子相关方法已经发展成熟，但很多时候无法正确描述共价键解离、双(多)自由基和激发态等电子之间相关性非常强的体系。近年来发展的多参考微扰理论和多参考耦合簇理论以多个行列式的线性组合为参考波函数，采用不同的方式有效考虑电子之间的动态相关，对强关联体系的描述取得了显著的改进。但根据理论出发点和精度要求的不同发展出了许多多参考理论，仍无一个公认的、令人满意的方案。本文将结合与常见电子相关方法在理论框架和计算精度上的比较，详细阐述块相关理论的基本原理，并介绍基于块相关的“另类”多参考电子相关方法。最后本文还简单展望了多参考电子相关方法今后的发展趋势。

多参考；块相关微扰理论；块相关耦合簇理论；多键解离；势能面

1 引 言

单参考(single reference，SR)电子相关方法是一类基于Hartree-Fock(HF)理论的post-HF方法，自上个世纪30年代后一直以迅猛的态势发展，并在过去几十年内日臻成熟，成为主流的从头算电子结构方法，广泛应用于分子的电子结构计算。这里所谓的单参考，即选取一个HF行列式为参考态波函数，再以不同的方式将电子从占据轨道激发至空轨道上或直接引入更多的激发组态，来考虑电子之间的动态相关。前者处理动态相关常见的方法为多体微扰理论(many-body perturbation theory or Møller–Plesset perturbation theory，MBPT或 MPn)和耦合簇理论(coupled cluster theory，CC)，后者则对应组态相互作用(configuration interaction，CI)方法。现在人们已经熟知，高效考虑动态相关的多体微扰理论和耦合簇理论可以在相同的计算标度下取得比组态相互作用方法更准确的计算结果，且计算结果具有大小一致性(截断的 CI方法不具备)，可用于均衡处理不同大小的体系。尤其是单参考 CC方法，在描述许多问题时已经能达到化学精度(4−10 kJ·mol−1)1。然而大量的计算表明，传统单参考方法只能精确描述势能面上位于平衡结构附近的情况。许多重要的化学问题如共价键的解离、分子结构的拉伸和畸变、有机分子中的双自由基或多自由基和光化学过程等等问题中，存在HOMO能级与LUMO能级简并或准简并的情况，这时电子之间的相关性非常强，一些组态与所选的单参考态可能占有同样的比重，体系具有内秉的多参考态特征。对这些问题，单参考方法无法准确描述其势能面，多体微扰方法的高阶微扰项绝对值很大，结果不合理。基于HF的CCSD和CCSD(T)方法通常也无法给出定性正确的结论1−3。针对这种情形，一种通常的方法是停留在单参考态框架内使用非限制性的 HF行列式(UHF)作为参考态波函数4−8。这种方法有时在能量上得到定性正确的结果，但是UHF带来的严重自旋污染(spin contamination)9−11问题，使得在此基础上考虑动态相关的多体微扰理论和耦合簇理论得到的结果同样有自旋污染，分子的各种性质难以得到描述。另一种途径便是超越单参考框架，发展以多个HF行列式为参考态的电子相关方法，并试图准确描述分子的各种性质。

如前所述，多参考(multireference，MR)电子相关方法即以多个行列式的线性组合为参考态波函数。若在此基础上分别采用微扰项或激发算符的指数形式考虑电子之间的动态相关，则分别对应于多参考微扰理论(MRPT)和多参考耦合簇理论(MRCC)。与单参考方法截然不同的是，多参考方法在无论在理论的公式推导上、编程的实现难度上，还是软件的使用方面，都比单参考方法复杂得多，且根据理论方法出发点和面对实际问题的不同衍生出许多变种方法，至今仍无一个公认的令人满意的多参考理论方案。最简单的多参考态波函数，可选取合适的活性轨道空间和活性电子数来构造，这就是完全活性空间自洽场(complete active space self-consistent field，CASSCF)波函数。Roos等人12发展的CASPT2方法便是基于CASSCF波函数的二阶微扰方法，能获得一定程度的动态相关。与单参考微扰方法类似，多参考微扰方法一般将零阶哈密顿算符定义成使零阶波函数为其本征函数，接着便可以使用微扰理论公式计算各阶波函数和校正能量。Mukherjee等人近年来发展的特定态多参考微扰理论(state-specific MRPT，SS-MRPT)13,14具有大小一致性(size-consistency)和无侵入态(intruder state)问题，在众多MRPT方法中比较有影响力。

相比单参考耦合簇理论，多参考耦合簇理论可以得到精度显著改善的结果。近年来发展的多参考耦合簇理论可以大致分为以下三类：(1)Hilbert空间或普遍态(state-universal，SU)多参考耦合簇理论15−19，每次处理的电子态中电子数目不变；(2) Fock空间或普遍价(valence-universal，VU)多参考耦合簇理论20−25，可以处理不同电子数目的电子态；(3) 特定态(state-specific)或选择态(state-selective，SS)多参考耦合簇理论26−30，每次处理一个特定的电子态。与SS-MRPT在微扰方法中的优势一样，SS-MRCC方法具有大小一致性和无侵入态问题，已经可以正确描述许多分子的解离势能面31，但其精度还没有达到公认的程度和较为理想的标准。另外，最直接的MRCC理论应当是以 CASSCF为参考波函数的 CAS-CCSD方法，考虑活性空间内所有组态函数对应行列式的单、双重外部激发。该方法以Ivanov和Adamowicz等人的出色工作32,33为代表，已经被证明对解离势能面有着高精度的描述，但其计算量惊人，经常用于理论上标定(benchmark)其他多参考方法，实际应用价值较小。另一方面，近年来还发展了一些“另类”多参考耦合簇策略(alternative MRCC methods)，试图用类似SRCC理论的框架提供新的解决方案。Li和Paldus发展的约化多参考耦合簇(reduced MRCC，RMR-CC)方法34−37利用 CC-CI方法的转化关系，从MRCI计算中引入近似的三、四重激发振幅并保持固定，而单、双重激发算符的振幅仍由CCSD提供，在迭代计算中是可变量。RMR-CCSD方法已经在不少具有多参考特征的体系上取得了较好的结果34,38。不同于上述所有基于轨道相关(orbital-based)的MRCC方法，我们课题组提出了一种基于块相关的多参考耦合簇理论(block-correlated coupled cluster theory ，BCCC)39−45。在该理论中我们将若干个轨道视为一个多轨道块(multi-orbital block)，即轨道集合的子集；单个轨道看成一个特殊的单轨道块(single-orbital block)。体系的波函数可以表示成各个块最重要的多电子态的张量积，再利用耦合簇激发算符将电子在块内进行激发或直接激发至别的块上，从而囊括块内的非动态相关能和块与块之间的动态相关能。若以CASSCF波函数为参考态，并将耦合簇算符截断至四块相关，对应的BCCC方法简称为 CAS-BCCC440,41。该方法计算量只比 CCSD略大，但精度优于 CASPT2和MR-CISD。

值得注意的是，无论是基于轨道相关的MRPT、MRCC还是基于块相关的CAS-BCCC4，多以CASSCF波函数为参考态，当活性空间增大时组态数目众多，计算量非常大，因此只能应用于较小的活性空间，这是这几类方法的一大限制。不过，块电子态和块相关的概念允许我们走出这一限制，将其推广至其他参考波函数上，比如广义价键(generalized valence bond，GVB)波函数46即是一种“类多参考”(MR-like)的波函数，可以作为参考态使用。结合完美配对的 GVB波函数(GVB-PP)46，我们课题组先后发展了 GVB-BCPT2方 法44和 CASCI-BCPT2/GVB 方 法45及DMRG-BCPT2/GVB方法45，将每个轨道对(geminal)视为一个块并以二阶微扰的形式考虑块与块之间的动态相关，大大增加了可处理的活性空间。本文将结合与多参考领域内其他方法的区别和联系，介绍我们课题组发展的基于块相关理论框架的MRPT和MRCC理论，并列举常见多参考研究体系的计算结果阐明目前方法的优势和不足，最后对多参考方法未来的发展方向做一些讨论。

2 块相关多参考方法

传统的单参考方法多以 HF行列式为参考波函数，在自旋轨道表示下，其二次量子化形式为

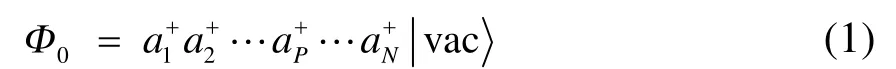
此时 Ai+I为块产生算符。显然，若包含多个自旋轨道，则其必定可以展开为多个行列式的线性组合；对应地，块产生算符 Ai+I应是该块内各自旋轨道产生算符乘积的线性组合。如果把每个块内最重要的电子态记为，则(1)式可以用块电子态的形式写为

其中M为块数。对一个占据单轨道块，其最重要的电子态(基态)即为其占据态，激发组态即为真空态(电子被激发至别的块内)；对于未占据单轨道块则情况恰好相反。而对于多轨道块，比如一含 4个自旋轨道的块，若允许其电子数在 0−4之间变化，总共可以有24= 16个电子态(包括真空态，详细表达式可以在Ref.40和Ref.44中找到)。另外，通过将多个块中任意一个块的电子态替换为它的某一个较高能量的电子态便可得单激发组态，形式如下：

式中 A1I为第I块的最重要电子态对应的块湮灭算符，多激发组态可以此类推。所以形如式(3)和(4)的波函数不仅可以表示单个HF行列式，还自然地包含了更为广义的内涵：通过选取合适的块，所有块产生算符作用在真空态上会产生多个行列式线性组合的效果。这为我们采用其他形式的参考波函数提供了便利条件，如以CASSCF为参考态，可以将整个活性空间视为一个块，其他自旋轨道均看作单轨道块；若以GVB波函数为参考态，则可以自然地将每个轨道对看作一个多轨道块，此时每个轨道块只包含 4个自旋轨道，电子数可以在0−4之间变化。

块相关耦合簇理论指的是将单参考理论框架中的单个自旋轨道的概念推广为一个多轨道块，并使用簇激发算符来处理块与块之间的动态相关。BCCC的波函数和指数算符表达式表观上和SRCC一样，

不同的是，有了块的概念之后簇激发算符就变为产生块内和块间电子的激发：

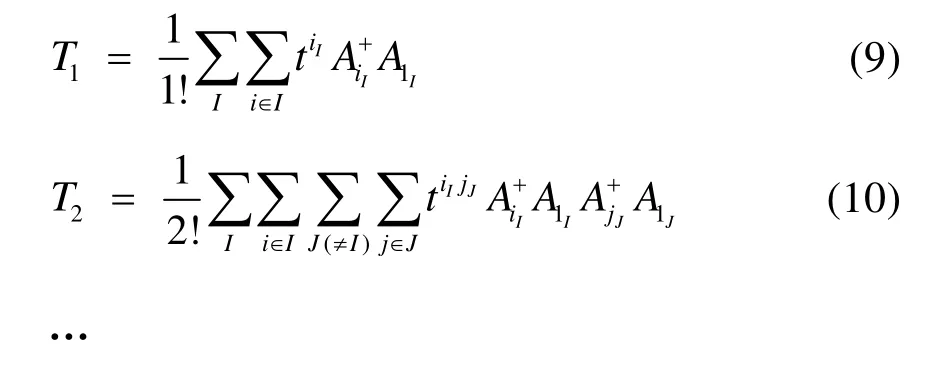
当簇激发算符截断至 n块时，对应的方法简记为BCCCn。从上述分析和式(6)−(10)可以看出，BCCC实际上是一种“另类”多参考耦合簇方法。块相关的概念不仅对 MRCC适用，对 MRCI和MRPT方法同样适用。另一方面，如同SRCC能够高效考虑动态相关的优点，BCCC理论上也是一种能够高效获得动态相关能的多参考方法。实际上早在BCCC理论第一次提出时，就已经被运用于一维或准一维的反铁磁性 Heisenberg模型基态能量的计算39，计算表明BCCC2能够得到准确基态能量值的 98.8%，BCCC3则可以得到比重99.5%以上的准确基态能量或 DMRG基态能量值(一维情况下DMRG结果极其接近准确值)。

2.1 CAS-BCCC4方法

前面已经提到，在 CAS-BCCC4中可以将参考态的活性空间视为一个多轨道块。此时参考态波函数实际上简化为

其中 i，j为占据自旋轨道指标。相应地，2T及更高阶的激发算符也会简化40。确定 CAS-BCCC4能量和各个激发振幅的方法与 SRCC类似，通过将Schrӧdinger方程投影到参考波函数和各激发组态函数可分别得到如下的非线性方程组：

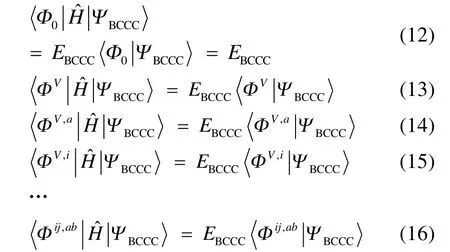
其中a，b为虚轨道指标，V为块电子态指标，且

其他组态函数的定义以此类推。振幅迭代公式采用类似SRCC方法中Hirata和Bartlett提出的迭代公式47。显然，上述公式的展开和化简比相应 SRCC的公式要繁琐得多，实际操作中相关公式通过采用计算机程序自动推导得出。由于电子的哈密顿算符中每一项至多只包含 4个单粒子算符(2个产生算符和2个湮灭算符)，所以将BCCC的簇激发算符截断至4块有其合理性：4块以上的激发组态函数与参考态波函数没有相互作用，对基态能量没有直接贡献。另外，CAS-BCCC4方法与单参考CCSD方法的紧密联系还有以下四点：第一，当参考态中唯一的多轨道块退化为一个自旋轨道时，CAS-BCCC4方程会相应地退化为CCSD方程。第二，从簇激发算符式(9)和(10)的形式可以看出，式(13)−(16)中的各个左矢波函数是各不相同的激发组态，不会出现相同的两个左矢，即方程个数等于未知变量(即左矢波函数)数目，这点与CCSD方程一致。第三，单参考CCSD方法的计算标度为N6，其中N为体系电子数；当活性空间大小固定而体系增大时，CAS-BCCC4方法的计算标度也为N6，这已在此前的文献40中详细讨论了。但是CAS-BCCC4方法比CCSD方法的标度“前因子”(prefactor)大，图1中两种方法分别计算不同碳数的链烷烃分子中单根碳碳键断裂时基态能量的计算时间随体系的增长情况可以反映出这一点(传统 CCSD方法的计算采用 Gaussian 09软件48)。第四，BCCC方法中各簇激发算符之间也是对易的，这点与CCSD的激发算符性质一样。当然，还可以通过e-THeT的Hausdorff展开式将N能量方程(12)和振幅方程(13)−(16)解耦合，不过目前我们在程序自动推导公式和编程中还没采取这种做法。而且我们的双电子积分变换代码没有经过详细地优化，这也是图 1中同一体系CAS-BCCC4计算时间较 CCSD时间长得多的原因之一。不过这些不足不会影响结果的准确性，在描述甲烷分子中 C―H单键解离和双原子分子N≡N三键的解离上，CAS-BCCC4方法已经十分接近完全组态相互作用(FCI)的结果(见表 1和图2)，可以定量描述键解离势能面。

常用非平行误差(nonparallelism errors，NPE)来衡量计算相对能量的精度。从表 1可以看出，针对 CH4单键解离势能面的计算，CAS-BCCC4给出的NPE值只有0.30 mH，说明该方法精度很高，且优于 MR-CISD。对 N≡N三键的解离，CAS-BCCC4方法对势能面的描述优于 MR-CISD和CASPT2方法，其NPE值为2.33，稍微大一些，但仍比另外两种方法要好不少(见图2中NPE值的比较)。

如果一个理论方法能够对键解离势能面给予高精度的描述，则它一定可以用来获得高精度的化学反应能垒。如图 3所示，环丁烯的开环反应中，反应物分子经由一个双自由基过渡态(TS)生成产物1,3-丁二烯，该TS具有明显的多参考特征，传统单参考方法一般难以得到可靠的描述。如图4所示，比较 CASSCF、MR-CISD、CASPT2和CAS-BCCC4四种方法计算得到的反应物能量和反应能垒，可以发现对反应物分子的基态电子能量，CAS-BCCC4给出的结果比其他三种方法都要低；对于反应能垒，除了 CASSCF，其余方法结果均与实验值((133.6 ± 0.8) kJ·mol−1)较为接近。总结CAS-BCCC4的特点：(1) 公式和理论框架十分接近 SRCC；(2) 计算量随 CAS空间的增大而急剧上升，但活性空间固定时与传统CCSD方法具有类似的计算标度；(3) 可以定量描述单键和多键的解离，精度高于CASPT2和MRCI方法。该方法的缺点也比较直观：由于采用CASSCF波函数为参考态，只能应用于活性空间较小的体系，且不具备严格的大小一致性。

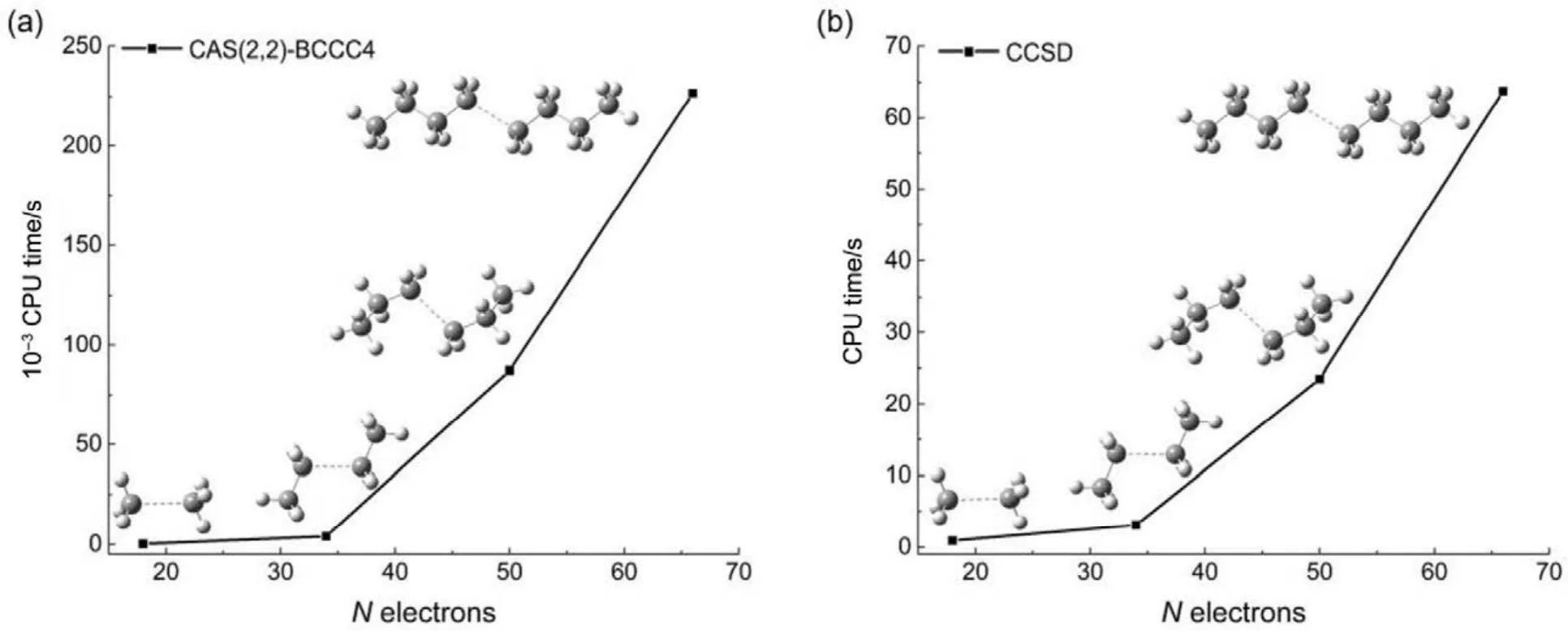
图1 烷烃分子中单根碳碳键断裂时CAS-BCCC4方法和CCSD方法计算体系基态能量的时间随体系增大的变化情况Fig.1 CPU time of CAS(2,2)-BCCC4 and CCSD method in calculating bond breaking ground state energies of different sizes of alkanes.

表1 CAS-BCCC4，MR-CISD和FCI三种方法计算甲烷分子中1根C―H键被拉长时基态电子能量的比较Table 1 Ground state energies calculated with CAS-BCCC4, MR-CISD and FCI methods for single C―H bond breaking in methane, at various bond distances.

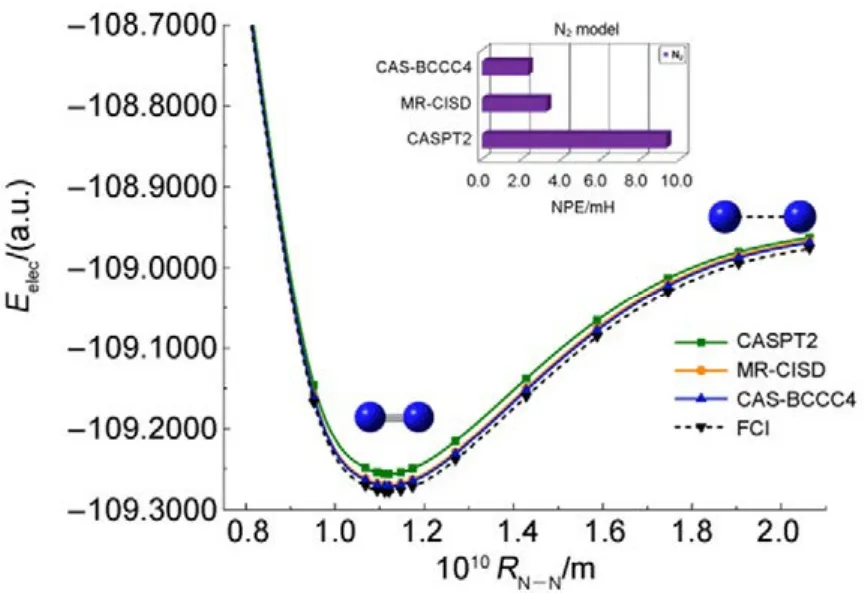
图2 N2分子解离势能面和能量精度比较Fig.2 Bond-breaking potential energy surface in N2.

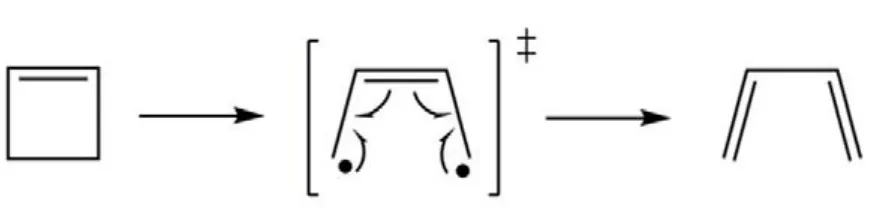
图3 环丁烯的开环反应Fig.3 Ring-opening reaction of 1-cyclobutene.

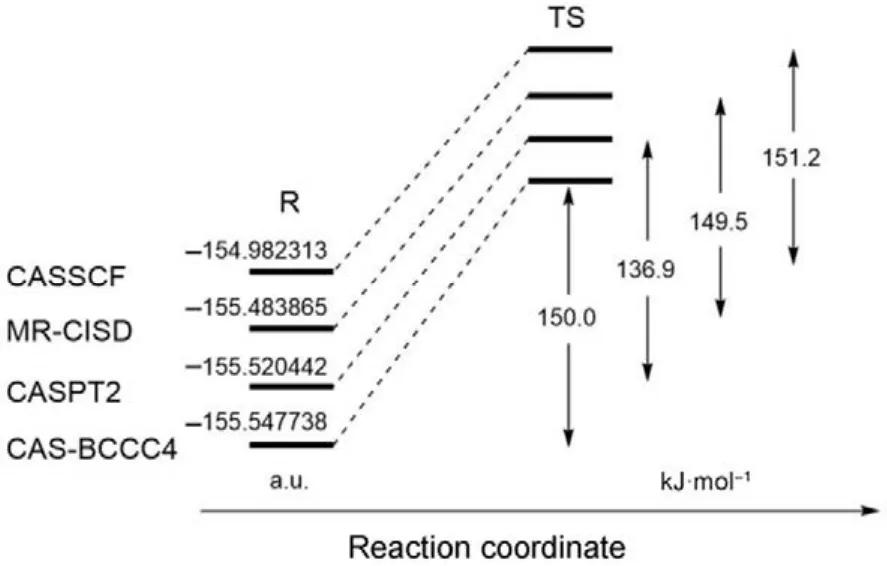
图4 采用不同多参考方法计算环丁烯开环反应中反应物分子能量和反应能垒的比较Fig.4 Comparison of the ground-state energies of the reactant and reaction barriers calculated using various MR methods.

2.2 GVB-BCPT2方法

GVB-PP波函数46分为三个部分：闭壳层芯轨道，轨道对和高自旋开壳层轨道部分，在自然轨道表示下可以写为式(19)和(20)的形式。其中为反对称化算符，所有的φ均为空间轨道，(σpi1,σpi

2)为第i个轨道对的系数(pair coefficients)。自旋函数Θ = α(1)β(2)α(3)β(4)…αα…α，遍历所有对和未成对电子。可以看出，上述波函数若展开可以表示为若干行列式的线性组合，因此GVB波函数带有多参考特征，可以看成是CASSCF波函数的一种近似45。GVB-BCPT2方法将每个轨道对视为一个块，利用激发算符将电子在块内产生激发或直接激发至别的块上，产生激发组态函数。块激发算符的形式在以前的工作44中已经给出(注意与BCCC的簇激发算符不同)。零阶波函数定义为每个块的基态电子态的乘积，再选取零阶哈密顿为各个块哈密顿算符的加和，就可以使零阶波函数为其本征函数，形式分别如下：其中指标r遍历所有虚轨道，λ遍历一个块内所有可能的电子态， EPλ对应块电子态的本征能量，由对角化块哈密顿矩阵得到。由于GVB波函数的特殊性，除了成对轨道构成的块是多轨道块(包含 4个自旋轨道)，其他块均为单轨道块(占据自旋轨道或虚轨道)，则有了零阶哈密顿，微扰算符即为 Vˆ = Hˆ - Hˆ0，二阶微扰能(不包括零阶和一阶能量)表达式为

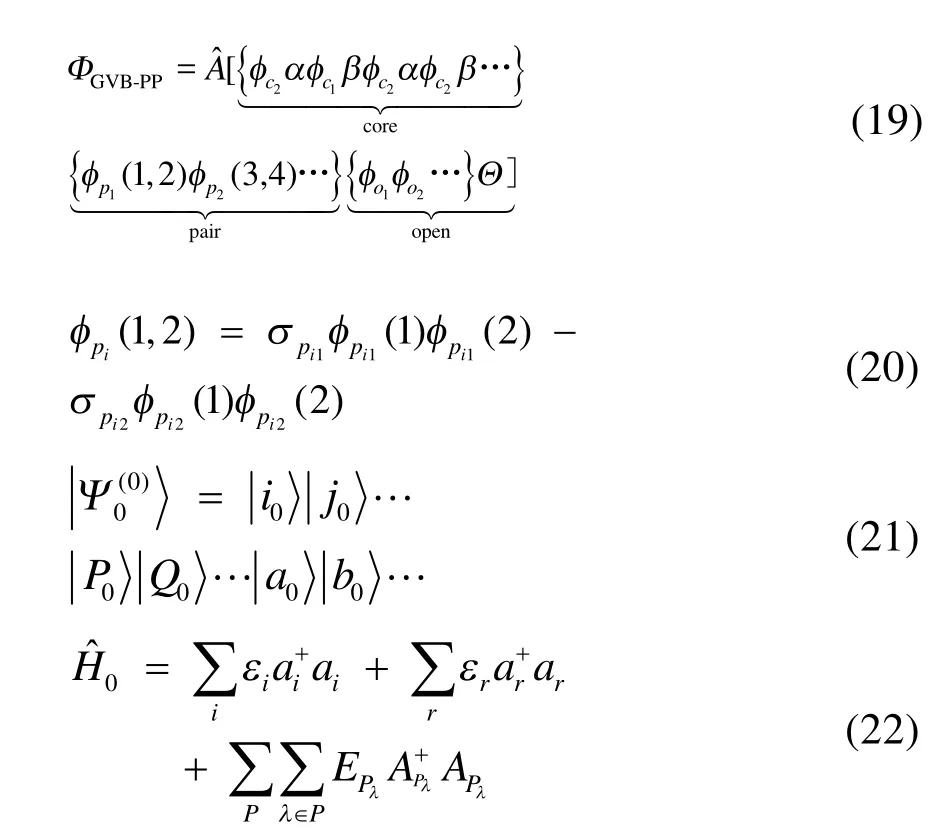
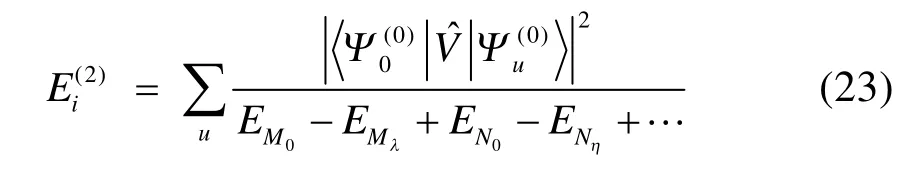
传统 MP2方法的计算量为 N5；而在GVB-BCPT2方法中，当挑选的轨道对数目一定时，随着体系电子数N的增加，该方法的计算标度也是N5级别44。但是同样地，后者比前者的标度“前因子”要大，所以计算时间更长。图 5中展示了两种方法对不同碳数的链烷烃分子中一根C―C键和一根末端C―H键同时断裂时基态能量的计算时间随体系的增长情况，可以反映出这一点。可以预期，GVB-BCPT2方法的精度应该比MP2结果有所改善，但仍不如CASPT2。图6中列出了三种方法计算双原子分子振动光谱常数的结果，可以看出采用带有多参考特征的GVB波函数作为参考态后，精度比MP2方法结果好，接近CASPT2的结果，符合理论预期。除此之外，GVB-BCPT2的明显优势还在于可以处理活性空间比CAS类方法大得多的体系。以一个强关联模型线性长链H50为例，将所有H―H距离拉伸时，活性空间必须包含全部50个电子，其中的组态数目是天文数字；但GVB采用25个轨道对来描述，可得到定性正确的结果。现有的基于CASSCF参考态的MR方法(如CASPT2)无法处理这样大的活性空间。图7展示了三种不同方法计算的H50解离势能面的NPE值(以DMRG方法为参考值标定)，很明显MP2精度在定性上存在问题，GVB本身能够给出相对合理的精度，而GVB-BCPT2对GVB约有50%的改善。

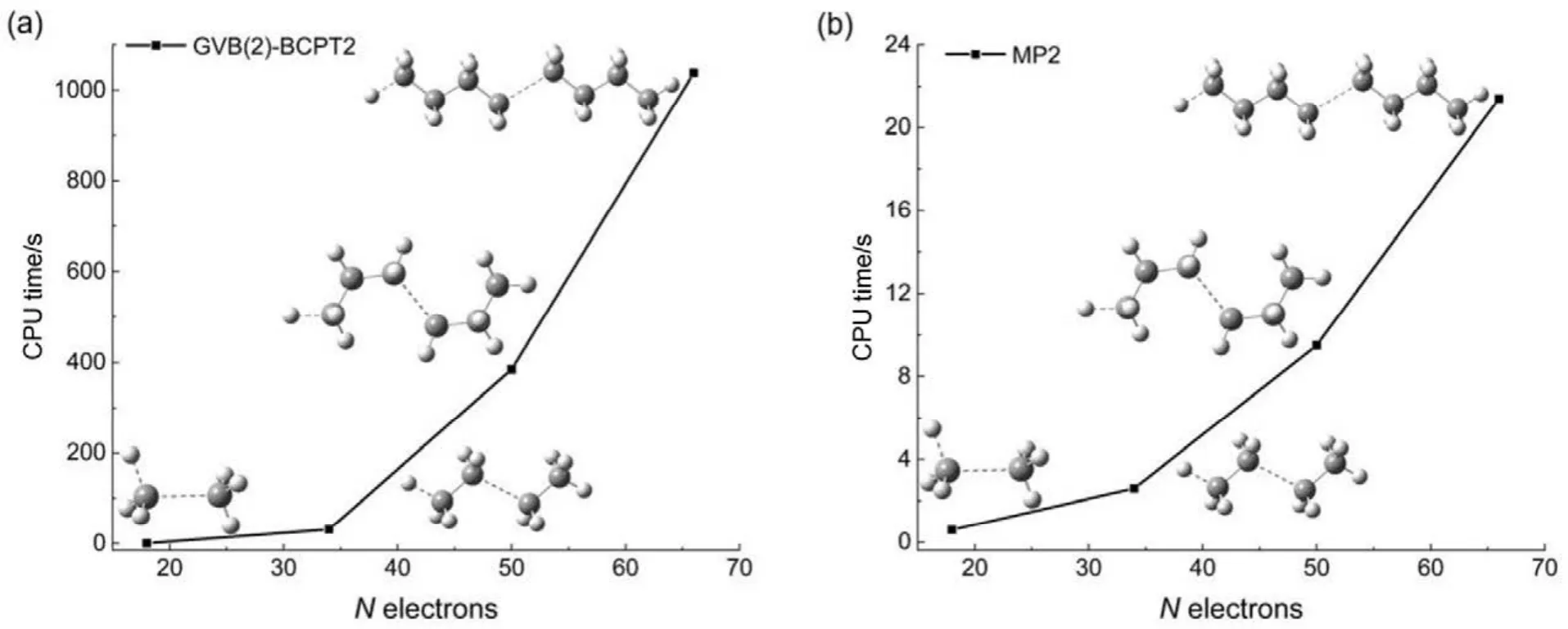
图5 烷烃体系中C―C单键和C―H单键同时断裂下GVB(2)-BCPT2和MP2方法计算基态能量的时间随体系电子数的增长情况Fig.5 CPU time of GVB(2)-BCPT2 and MP2 method in calculating bond breaking ground state energies of different sizes of alkanes.

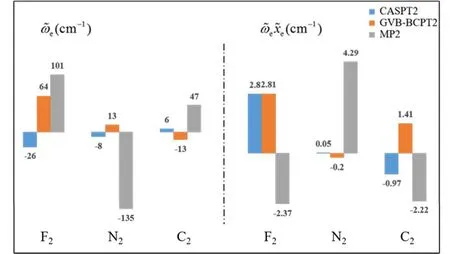
图6 不同理论方法计算的几种双原子分子振动光谱常数与实验值偏差的比较Fig.6 Deviations of computed spectroscopic constants with respect to experimental values for the ground state of several diatomic molecules.

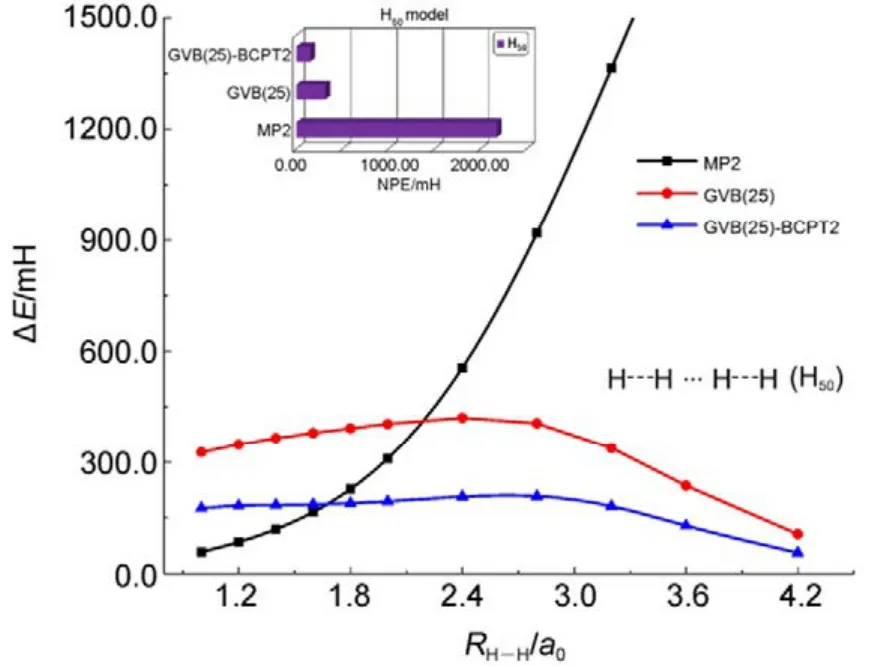
图7 不同方法计算线性长链H50中所有键同时解离势能面的精度Fig.7 Accuracy of different methods in calculating simultaneous bond dissociation potential energy surface in linear chain H50.

归纳GVB-BCPT2的优点：(1) 轨道对数目固定时，计算量类似于 MP2；(2) 可处理的活性空间大小超越基于CAS的MR方法。但是该方法也有缺点，对一些多键解离体系的计算结果表明GVB-BCPT2的能量无法收敛44,45，一个原因是存在一些轨道对的基态能量与激发组态能量非常接近(准简并)，导致分母接近零而使结果误差很大(MP2同样有此问题)。可能的解决办法是发展可高效考虑动态相关的GVB-BCCC4方法，我们课题组正在开展这方面的理论工作。

2.3 CASCI-BCPT2/GVB方法和

DMRG-BCPT2/GVB方法

如上所述，GVB-BCPT2方法不能处理多键解离的主要原因是微扰理论难以处理多键解离时几个轨道对之间很强的动态相关。一个改进的思路是将强关联的轨道对之间的电子相关用变分方法处理，而将轨道对与其它轨道之间的电子相关用GVB-BCPT2中类似的方法处理。CASCI-BCPT2/GVB45这种杂化方法正是基于这个思路，对CAS/A49方法的动态相关能用近似的方法计算。例如，CAS/A的能量表达式为

上述等式右边第二项涉及动态相关，但由于CAS/A考虑了活性空间内所有可能的组态，只能应用于活性空间非常小的体系。若将其中的CASCI参考态替换为GVB参考态，对应的激发组态替换为 GVB-BCPT2中块激发算符产生的激发组态，总能量简化为如下形式

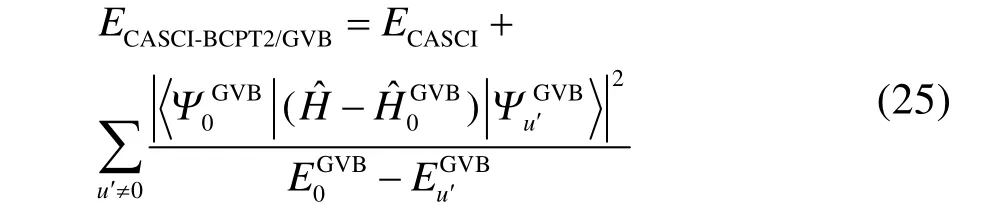
上式中右边第二项相比式(24)中右边第二项，计算量大大降低。此处有两点需要说明：第一，在计算第二项的动态相关时，求和项中不包括轨道对之间激发算符产生的激发组态，因为这部分的贡献已经包含在第一项中；第二，式(24)中求和指标u是遍历活性空间内所有的激发组态；而式(25)中求和指标u′是遍历各轨道对内激发组态，通过多个低激发算符的乘积可以耦合出高激发组态，从而在CAS/A中的高激发组态对应矩阵元的计算简化为在 GVB-BCPT2中若干个低激发组态对应矩阵元的乘积，即矩阵元的计算大大简化，故而计算量降低。将上式中的 ECASCI替换为密度矩阵重整化群(density matrix renormalization group，DMRG)参考态的能量 EDMRG，即得到DMRG-BCPT2/GVB方法45的总能量定义式。这两种杂化方法中，前者可以看作是对CAS/A方法的近似，后者则可以视为对单纯的DMRG方法的改进。不过，这种“杂化”式的改进与近年来发展的直接基于DMRG参考态波函数，再引入外部动态相关的密度矩阵重整化群-活性空间二阶微扰(DMRG-CASPT2)50、密度矩阵重整化群-正则变换(DMRG-CT)51、密度矩阵重整化群-强简缩N电子价态二阶微扰(DMRG-SC-NEVPT2)52和矩阵乘积态-线性化耦合簇(MPS-LCC)53等等“纯”post-DMRG方法又有不同：DMRG-BCPT2/GVB方法的静态相关项是由 DMRG参考态获得的，而其动态相关项是用GVB参考态去近似得出的；但是上述几种 post-DMRG方法不仅静态相关能由DMRG获得，其动态相关能也是直接在DMRG参考态基础上作激发得到的。当然，这些post-DMRG方法与我们的方法异曲同工，都能处理活性空间大得多的体系。例如，过渡金属双原子分子Cr2定量正确的解离势能面已经有DMRG-CASPT2(12,28)50和DMRG-SC-NEVPT2(12,22)方法52报道过了。

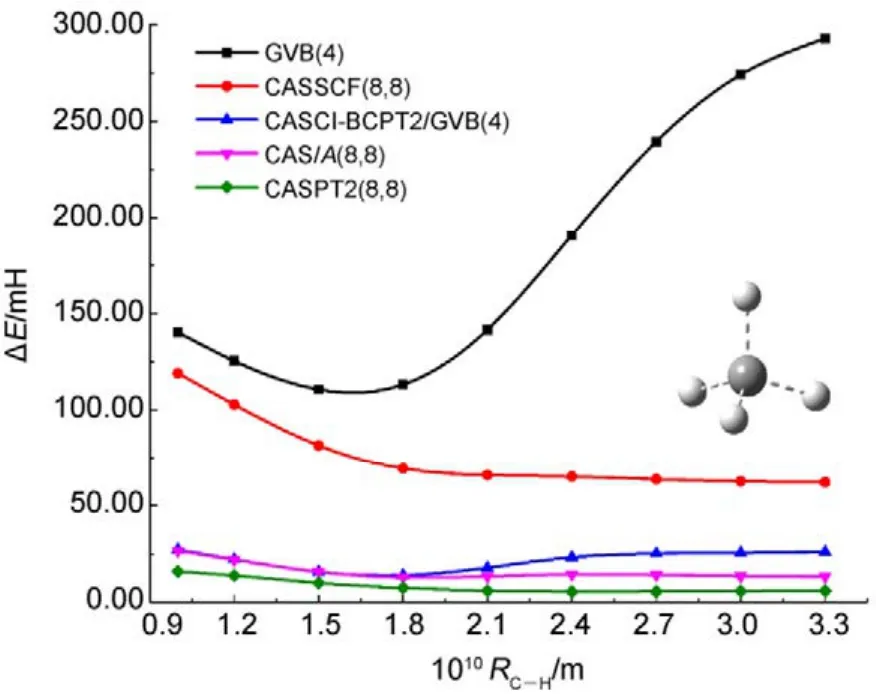
图8 不同方法计算甲烷分子中所有单键同时解离的势能面Fig.8 Potential energy surfaces for simultaneous bond dissociation in CH4, calculated with various methods.

图9 不同方法计算正丁烷分子中所有单键同时解离的势能面Fig.9 Potential energy surfaces for simultaneous bond dissociation in n-butane, calculated with various methods.

图8和图9中列出了分别使用两种方法计算CH4和正丁烷(C4H10)分子中所有单键同时解离的势能面。如图 8所示，CASCI-BCPT2/GVB与CAS/A计算的电子能量和精度均非常接近(NPE分别为13.20和13.87)，比单纯的GVB或CASSCF的结果要好很多。当然，CASPT2的精度更高。但如前所述，CASPT2计算量更大，处理CH4中4根单键同时断裂的活性空间尚合适，处理 C4H10分子中13根单键同时解离时则不适用，因为此时需要 CASSCF(26,26)作为参考波函数。这时可以采用DMRG-BCPT2/GVB方法，GVB参考态则选为GVB(13)，即包含13个轨道对。从图9可看出，GVB(13)-BCPT2给出的精度已经不如单纯的DMRG(26,26)方法，而 DMRG(26,26)-BCPT2/GVB(13)对 DMRG(26,26)的结果又可以有超过60%的改善(相对于非常精确的DMRG(26,52)的结果)，说明该方法描述动态相关是比较有效的。以上的结果表明基于 GVB参考态的CASCI-BCPT2/GVB或DMRG-BCPT2/GVB能够在 GVB基础上比较有效地描述动态相关能。然而，当研究体系的轨道局域化程度较差时，GVB波函数便不太适合用作参考态，此时用这两种方法所得的计算精度会有所下降，一些体系的计算结果45已经验证了这种问题的存在。

3 结 论

本文详细介绍了在块相关理论框架下块相关微扰理论和块相关耦合簇理论的基本思想和相关的理论公式。块的概念是整个块相关理论框架的基石：将若干个自旋轨道视为整体，即一个块，电子相关问题转化为块相关问题，体系的零阶波函数写为各个块最重要电子态的张量积，激发组态的构建采用块内或块间电子的激发，由此便可自然地发展出块相关微扰理论和块相关耦合簇理论。这两种多参考理论在公式和计算标度上类似于传统的单参考理论，具有其他多参考方法难以替代的优点。以 CASSCF波函数为参考态，CAS-BCCC4方法可以定量描述单键和多重键的解离，十分接近 FCI的结果，但只能处理较小的活性空间。以 GVB 波函数为参考态的GVB-BCPT2方法能够处理体系中许多单键的同时解离，所涉及的活性空间大小超越常规多参考方法(如CASPT2)的极限，但精度有所下降，不如CASPT2。而在GVB-BCPT2的基础上，两种改良方案CASCI-BCPT2/GVB和DMRG-BCPT2/GVB方法可以对中等大小活性空间的体系给出优于GVB-BCPT2的描述，大幅提高了计算精度。但无论是这两种改良方法，还是适合较小活性空间的更高精度的 CAS-BCCC4方法，都不意味着块相关理论的能力极限。相反，基于块相关理论处理多参考问题的巨大潜力，相信未来会发展出适用大活性空间的高精度块相关电子结构新方法。

4 展 望

近二三十年高精度电子结构方法的发展表明，单参考电子相关方法已经成熟，黑箱式的程序已经可让用户很方便地使用。当HF行列式是合适的参考态时，单参考方法能给出令人满意的结果。但是对具有多参考特征的体系，如何以稍大于单参考方法的计算量来给出定量正确的结果，并尽量减少运行程序时的人为干预，仍然是今后多参考方法研究的重点和难点。对于MRPT理论，一方面需要继续寻找符合大小一致性的微扰理论框架；另一方面，发展更高阶的微扰理论同时尽量确保总能量随微扰项的增加而改善，也是一个很有挑战性的方向。而对于MRCC理论，直接以CASSCF为参考态的多参考方法面临无法处理较大活性空间的难题，发展以更紧凑形式表示组态、更有效考虑激发组态的理论方法十分诱人；发展基于UHF、GVB和APSG(antisymmetric product of strongly orthogonal geminals)54,55等参考波函数的“另类”MRPT和MRCC方法也许是一条扩大可处理活性空间的有效途径。在应用方面，定量描述分子的激发态和双(或多)自由基反应的能垒、理论模拟各种分子光谱(如IR、Raman和NMR谱等)和处理凝聚相或周期性体系等热点问题也势必将成为多参考方法大显身手的舞台。

致 谢:文中部分计算在南京大学高性能计算中心完成。

(1) Lyakh, D. I.; Musiał, M.; Lotrich, V. F.; Bartlett, R. J. Chem. Rev.2012, 112 (1), 182. doi: 10.1021/cr2001417

(2) Włoch, M.; Gour, J. R.; Piecuch, P. J. Phys. Chem. A 2007, 111 (44),11359. doi: 10.1021/jp072535l

(3) Bartlett, R. J. WIREs Comput. Mol. Sci. 2012, 2 (1), 126.doi: 10.1002/wcms.76

(4) Amos, R. D.; Andrews, J. S.; Handy, N. C.; Knowles, P. J. Chem.Phys. Lett. 1991, 185 (3–4), 256.doi: 10.1016/S0009-2614(91)85057-4

(5) Murray, C.; Davidson, E. R. Chem. Phys. Lett. 1991, 187 (5), 451.doi: 10.1016/0009-2614(91)80281-2

(6) Jayatilaka, D.; Lee, T. J. J. Chem. Phys. 1993, 98 (12), 9734.doi: 10.1063/1.464352

(7) Szalay, P. G.; Gauss, J. J. Chem. Phys. 1997, 107 (21), 9028.doi: 10.1063/1.475220

(8) Chen, F. J. Chem. Theory Comput. 2009, 5 (4), 931.doi: 10.1021/ct800546g

(9) Wheeler, S. E.; Allen, W. D.; Schaefer, H. F. J. Chem. Phys. 2008,128 (7), 074107. doi: 10.1063/1.2828523

(10) Krylov, A. I. J. Chem. Phys. 2000, 113 (15), 6052.doi: 10.1063/1.1308557

(11) Chen, F. W.; Wei, M. J.; Liu, W. J. Sci. China Chem. 2011, 54 (3),446. doi: 10.1007/s11426-010-4199-1

(12) Andersson, K.; Malmqvist, P. Å.; Roos, B. O. J. Chem. Phys. 1992,96 (2), 1218. doi: 10.1063/1.462209

(13) Sinha Mahapatra, U.; Datta, B.; Mukherjee, D. J. Phys. Chem. A 1999, 103 (12), 1822. doi: 10.1021/jp9832995

(14) Chattopadhyay, S.; Chaudhuri, R. K.; Mahapatra, U. S.; Ghosh, A.;Ray, S. S. WIREs Comput. Mol. Sci. 2016, 6 (3), 266.doi: 10.1002/wcms.1248

(15) Jeziorski, B.; Monkhorst, H. J. Phys. Rev. A 1981, 24 (4), 1668.doi: 10.1103/PhysRevA.24.1668

(16) Meissner, L.; Jankowski, K.; Wasilewski, J. Int. J. Quantum Chem.1988, 34 (6), 535. doi: 10.1002/qua.560340607

(17) Balková, A.; Kucharski, S. A.; Meissner, L.; Bartlett, R. J. Theor.Chim. Acta 1991, 80 (4), 335. doi: 10.1007/bf01117417

(18) Li, X.; Paldus, J. J. Chem. Phys. 2003, 119 (11), 5320.doi: 10.1063/1.1599283

(19) Hanrath, M. J. Chem. Phys. 2005, 123 (8), 084102.doi: 10.1063/1.1953407

(20) Offermann, R.; Ey, W.; Kümmel, H. Nucl. Phys. A 1976, 273 (2), 349.doi: 10.1016/0375-9474(76)90596-0

(21) Offermann, R. Nucl. Phys. A 1976, 273 (2), 368.doi: 10.1016/0375-9474(76)90597-2

(23) Kutzelnigg, W. J. Chem. Phys. 1982, 77 (6), 3081.doi: 10.1063/1.444231

(24) Hughes, S. R.; Kaldor, U. Chem. Phys. Lett. 1992, 194 (1), 99.doi: 10.1016/0009-2614(92)85749-Z

(25) Meissner, L.; Malinowski, P. Phys. Rev. A 2000, 61 (6), 062510.doi: 10.1103/PhysRevA.61.062510

(26) Hubač, I.; Neogrády, P. Phys. Rev. A 1994, 50 (6), 4558.doi: 10.1103/PhysRevA.50.4558

(27) Mášik, J.; Hubač, I.; Mach, P. J. Chem. Phys. 1998, 108 (16), 6571.doi: 10.1063/1.476071

(28) Mahapatra, U. S.; Datta, B.; Bandyopadhyay, B.; Mukherjee, D. In Advances in Quantum Chemistry, Per-Olov, L., Ed.; Academic Press:San Diego, CA, 1998; Vol. 30, pp 163. doi:10.1016/S0065-3276(08)60507-9

(29) Mahapatra, U. S.; Datta, B.; Mukherjee, D. J. Chem. Phys. 1999, 110(13), 6171. doi: 10.1063/1.478523

(30) Chattopadhyay, S.; Pahari, D.; Mukherjee, D.; Mahapatra, U. S. J.Chem. Phys. 2004, 120 (13), 5968. doi: 10.1063/1.1650328

(31) Kӧhn, A.; Hanauer, M.; Mück, L. A.; Jagau, T.-C.; Gauss, J. WIREs Comput. Mol. Sci. 2013, 3 (2), 176. doi: 10.1002/wcms.1120

(32) Lyakh, D. I.; Ivanov, V. V.; Adamowicz, L. J. Chem. Phys. 2005, 122(2), 024108. doi: 10.1063/1.1824897

(33) Lyakh, D. I.; Ivanov, V. V.; Adamowicz, L. Mol. Phys. 2007, 105(10), 1335. doi: 10.1080/00268970701332539

(34) Li, X.; Paldus, J. J. Chem. Phys. 1997, 107 (16), 6257.doi: 10.1063/1.474289

(35) Li, X.; Paldus, J. Mol. Phys. 2000, 98 (16), 1185.doi: 10.1080/00268970050080546

(36) Li, X.; Paldus, J. J. Chem. Phys. 2006, 124 (17), 174101.doi: 10.1063/1.2194543

(37) Li, X.; Paldus, J. J. Chem. Phys. 2006, 125 (16), 164107.doi: 10.1063/1.2361295

(38) Li, X.; Paldus, J. J. Chem. Phys. 1998, 108 (2), 637.doi: 10.1063/1.475425

(39) Li, S. J. Chem. Phys. 2004, 120 (11), 5017. doi: 10.1063/1.1646355

(40) Fang, T.; Li, S. J. Chem. Phys. 2007, 127 (20), 204108.doi: 10.1063/1.2800027

(41) Fang, T.; Shen, J.; Li, S. J. Chem. Phys. 2008, 128 (22), 224107.doi: 10.1063/1.2939014

(42) Shen, J.; Fang, T.; Hua, W.; Li, S. J. Phys. Chem. A 2008, 112 (20),4703. doi: 10.1021/jp7118907

(43) Shen, J.; Fang, T.; Li, S.; Jiang, Y. J. Phys. Chem. A 2008, 112 (48),12518. doi: 10.1021/jp807183m

(44) Xu, E.; Li, S. J. Chem. Phys. 2013, 139 (17), 174111.doi: 10.1063/1.4828739

(45) Xu, E.; Zhao, D.; Li, S. J. Chem. Theory Comput. 2015, 11 (10),4634. doi: 10.1021/acs.jctc.5b00495

(46) Bobrowicz, F. W.; Goddard, W. A. In Methods of Electronic Structure Theory; Schaefer, H. F. Ed.; Springer US: Boston, MA, 1977; p 79.doi: 10.1007/978-1-4757-0887-5_4

(47) Hirata, S.; Bartlett, R. J. Chem. Phys. Lett. 2000, 321 (3–4), 216.doi: 10.1016/S0009-2614(00)00387-0

(48) Frisch, M. J. T., G. W.; Schlegel, H. B.; et al. Gaussian 09, Revision B.01, Gaussian Inc.: Wallingford, CT, 2009.

(49) Dyall, K. G. J. Chem. Phys. 1995, 102 (12), 4909.doi: 10.1063/1.469539

(50) Kurashige, Y.; Yanai, T. J. Chem. Phys. 2011, 135 (9), 094104.doi: 10.1063/1.3629454

(51) Yanai, T.; Kurashige, Y.; Neuscamman, E.; Chan, G. K. L. J. Chem.Phys. 2010, 132 (2), 024105. doi: 10.1063/1.3275806

(52) Guo, S.; Watson, M. A.; Hu, W.; Sun, Q.; Chan, G. K.-L. J. Chem.Theory Comput. 2016, 12 (4), 1583. doi: 10.1021/acs.jctc.5b01225

(53) Sharma, S.; Alavi, A. J. Chem. Phys. 2015, 143 (10), 102815.doi: 10.1063/1.4928643

(54) Zoboki, T.; Szabados, Á.; Surján, P. R. J. Chem. Theory Comput.2013, 9 (6), 2602. doi: 10.1021/ct400138m

(55) Jeszenszki, P.; Nagy, P. R.; Zoboki, T.; Szabados, Á.; Surján, P. R. Int.J. Quantum Chem. 2014, 114 (16), 1048. doi: 10.1002/qua.24634

Multireference Perturbation Theory and Multireference Coupled Cluster Theory Based on the “Block-Correlation” Framework

ZOU Jing-Xiang1SHEN Jun2XU En-Hua3FANG Tao1LI Shu-Hua1,*
(1School of Chemistry and Chemical Engineering, Key Laboratory of Mesoscopic Chemistry of Ministry of Education, Institute of Theoretical and Computational Chemistry, Nanjing University, Nanjing 210023, P. R. China;2Department of Chemistry,Michigan State University, East Lansing, Michigan 48824, United States;3Graduate School of System Informatics,Kobe University, Kobe, Hyogo 657-0025, Japan)

Well-developed conventional single-reference electron-correlation methods usually fail to describe the dissociation of covalent bonds, di(or poly)radical systems or electronic structures of the excited states. Based on a multi-determinantal wave function, recently emerged multireference perturbation theories and coupled cluster theories can give drastically improved results; however, there is still no satisfactory scheme so far. In this monograph, alternative multireference perturbation theories and coupled cluster theories based on the “block-correlation” framework has been introduced and illustrated in detail, together with proper comparisons with other common electron-correlation methods. Future perspectives upon multireference theories have also been briefly discussed.

Multireference; Block-correlated perturbation theory; Block-correlated coupled cluster theory; Multiple bond dissociation; Energy potential surface

December 1, 2016; Revised: March 21, 2017; Published online April 7, 2017.

O641.12

10.1016/0375-9474(78)90068-4

[Feature Article]

10.3866/PKU.WHXB2017040702 www.whxb.pku.edu.cn

*Corresponding author. Email: shuhua@nju.edu.cn; Tel: +86-25-89686465.

The project was supported by the National Natural Science Foundation of China (21333004, 21673110).国家自然科学基金(21333004, 21673110)资助项目

© Editorial office of Acta Physico-Chimica Sinica

邹竞祥，南京大学化学化工学院物理化学专业博士研究生。2015年于南京大学匡亚明学院获理学学士学位。主要研究兴趣为多参考态耦合簇理论和化学反应机理的自动化搜索。

沈军，2008年于南京大学化学化工学院获理学博士学位。2010年至今于美国密歇根州立大学工作，现为该校化学系研究助理。主要研究方向为高精度电子相关方法的发展及应用。

方涛，2008年于南京大学化学化工学院获理学博士学位。2008−2012年在日本量子化学研究所工作。主要研究方向包括多参考态耦合簇理论和大分子体系的分片方法。

许恩华，2011年于南京大学化学化工学院获理学博士学位。现于日本神户大学从事博士后研究工作，主要研究方向为多参考态微扰理论和多参考态耦合簇理论。

黎书华，南京大学教授，博士生导师，教育部“长江学者”特聘教授，2014年当选世界理论与计算化学家协会理事会理事。主要研究领域为线性标度量子化学计算方法、多参考态电子相关方法和无机及有机金属反应的理论研究。