相控阵超声检测声场近场区长度的理论
,,,, ,
(1.河海大学 物联网工程学院,常州 213022;2.江苏省特种设备安全监督检验研究院,常州 213016;3.中国石油锦西石化公司机械厂,葫芦岛 125001;4.中国特种设备检测研究院,北京 100013)
相控阵超声检测声场近场区长度的理论
姜学平1,岳云飞2,庄凤冬3,毛小虎2,郑晖4,韩庆邦1
(1.河海大学物联网工程学院,常州213022;2.江苏省特种设备安全监督检验研究院,常州213016;3.中国石油锦西石化公司机械厂,葫芦岛125001;4.中国特种设备检测研究院,北京100013)
相控阵超声检测技术可靠高效、无辐射,可应用于工业无损检测中。对于均匀各向同性材料工件,尤其是焊缝的相控阵超声检测,可采用超声斜入射脉冲横波扇形扫描检测的方法。探讨相控阵超声探头辐射不同偏转角度声场的近场区长度问题,进行了理论计算和仿真分析,发现焊缝检测中常用有机玻璃楔块角度为36.2°时,偏转角度越大,近场区长度越小。结果可为相控阵超声检测工艺设计和检测设备校准提供参考。
相控阵超声检测;扇形扫描;近场区长度;聚焦声波
伴随着材料、微加工、计算机和电子技术的迅速发展,相控阵超声检测技术越来越多地应用于工业无损检测中,这是由于其具有检测所用声束灵活可控,检测可靠、高效、受人为因素影响小、无辐射无污染、检测结果直观、可保存[1]的优点。相关理论的逐渐完善[2-6]、检测方法的不断丰富[7-12],以及国内外相关标准、设备、软件的逐步被认可、应用[13-14],特别是近两年来该技术现场试验的成功应用,大大推动了相关行业标准形成的进程,进一步加快了该技术的发展与应用。
相控阵超声检测中,可以采用超声斜入射脉冲横波回波法,设置探头位置和检测所用声束的扇形扫描角度范围实现待测区域的全部检测。其中,在声场的近场范围内,声波可以有效聚焦,所以常采用相控聚焦方法提高检测精度;在远场采用非聚焦声场,减小声束发散角,提高检测横向分辨力。因此需要研究相控阵超声检测中声场的分布特性,以指导检测方法与工艺的研究。强天鹏[15]等给出了近场区长度计算方法,并测量了近场区长度对聚焦法则的变化规律,但未考虑楔块角度,且计算需要修正因子。孙芳[16]等将带有楔块的相控阵超声检测问题简化为液-固界面上的声传播问题,推导了平面波入射液-固界面的声透射系数。张迪等研究了薄板相控阵超声检测中Lamb波声场的分布特性[17]。周正干等[18]研究了相控阵超声检测L形工件时的检测声场。姜学平等计算了不同入射角度下,声波在楔块-工件界面的透射系数,结合实际应用给出扇形扫描折射角度范围为38°~75°的建议值,推导了声波在不同位置聚焦时各阵元相对延时的解析计算公式[19-20]。但目前对相控阵超声检测声场近场区长度的计算研究相对较少,由于声场只能在近场区聚焦,所以这个长度对检测工艺设计中是否采用聚焦声场检测有较重要的参考作用。
文章基于几何声学的方法,通过计算相控阵超声探头辐射不同角度偏转声束的有效声辐射口径,推导偏转声束近场区长度与探头的声辐射口径和楔块相关参数的关系;采用半解析的数值计算方法仿真声场,观测近场区长度,仿真结果与理论推导计算结果吻合。
1 相控阵探头楔块偏转声场的近场区长度解析计算
一般情况下,均匀各向同性材料工件,特别是在焊缝的相控阵超声检测中,探头辐射声场至楔块中,经楔块、楔块-工件滑移界面,在界面上发生模式转换后,产生横波进入待检工件中。
该部分的推导是基于几何声学假设进行的。声束由声线表示,各声线独立传播,声线会发生折射、反射、衍射和衰减等。这里只考虑声波折射的情况。利用声线追踪法(几何声学法)可以近似计算声场近场区长度,辅助检测工艺设计。

图1 线性相控阵探头辐射偏转声场近场区长度计算示意
图1为线性相控阵探头辐射偏转声场近场区长度计算示意。如图1所示,一维线性相控阵超声换能器激活口径(active aperture)为A0,楔块倾斜角度为α,Li为声波沿着声轴线在楔块中传播的距离,楔块中的纵波声速为cw,工件中声速为cs,声频率为f。假定某延时法则使声束在工件中的折射角为θt,此时楔块中等效的声辐射口径由原来的A0变为Aw,入射角为θi。这里,下标i表示入射波,t表示透射波。根据Snell定律,可得:
由几何关系,得:
当折射角为θt时,将相控阵探头通过楔块向待检测工件中辐射偏转声场类比为探头向单一介质中辐射声场,类比探头对应的口径为有效声辐射口径Aeff:
设待检测工件中的声波长为:
探头向单一介质中辐射声场的近场区长度可以表示为[21]:
将式(2),(3)和(4)代入式(5)中,减去声波在楔块中传播的等效距离,即可得到相控阵探头联合斜楔块组合系统辐射偏转波时,在待检测工件中的近场区长度为:
比起近场区长度,检测中更常用的是检测深度,所以计算近场区深度为:
由式(6)可见,相控阵偏转声场近场区长度与频率、工件中的声速、探头声辐射口径、楔块角度和偏转角度有关。其他条件不变的情况下,探头声辐射口径越大,近场区长度越大;工件中声波λt越大,近场区长度越小;对于材料确定的工件的检测,频率越高,近场区长度越大,有效聚焦范围越大,但实际检测中频率的确定,需要考虑材料引起的信噪比和声衰减影响;而近场区长度随偏转角度的变化,从公式中不易看出,可通过计算进行讨论。
设工件中的声传播速度ct=3 236 m·s-1,ci=2 330 m·s-1,Li=12.3 mm,A0=9.50 mm,α=36.2°,f=5.0 MHz,实际检测中一般用负方波脉冲激励换能器辐射声波,将方波脉冲宽度乘以2后求倒数约定为检测声场频率f,声束偏转35°~72°时近场区长度和偏转角度的关系曲线见图2。

图2 36°~72°偏转下近场区长度/近场区深度和折射偏转角度的关系曲线
由图2可见,一般的焊逢检测中,折射角为36°~72°的情况下,当相控阵探头和楔块确定时,偏转角度越大,近场区长度越小,声场可以有效聚焦的范围就越小。
2 相控阵探头楔块偏转声场的近场区长度仿真分析
声场仿真采用铅笔法的半解析计算。将声辐射面上的各点视为点声源,求解区域离散成点阵;在弹性介质中,距点源足够远的计算点(即场点)处声波近似为平面波,平面波的振幅随着传播距离的增加而不断减小;从探头各阵元发出的声波经过楔块、楔块-工件平面滑移接触面后进入待检测工件中,场点处的声振幅即为各个点声源在该点贡献的叠加[22];计算求解域中各点的声压,最后得到声场分布。采用的工件的参数为:尺寸(长×宽×高),300 mm×200 mm×150 mm;横波声速,3 236 m·s-1;纵波声速,5 916 m·s-1;密度,7.8 g·cm-3。由于工件材料各向同性,且在钢中传播距离较短,故忽略声衰减。探头的详细参数为:矩形阵元间距,0.6 mm;阵元个数,16;单个阵元长度,10 mm;激活口径,9.5 mm。楔块的各方向尺寸示意见图3。楔块材料为有机玻璃,其详细参数为:横波声速,1 136 m·s-1;纵波声速,2 330 m·s-1;密度,1.18 g·cm-3;L1,9.72 mm;L2,13.30 mm;L3,23.0 mm;L4(即Li),12.3 mm;入射角α,36.2°。计算参数为:偏转角度,35°~75°(第一临界角时,折射横波的折射角度为33°,需要避免声速的变化引起钢中出现纵波);计算横波分布区域,80 mm×42 mm。计算折射角角度分别为45°、50°、55°和60°时的声场,其中当折射角为55°时,各阵元没有相对延时。仿真结果见图3。

图3 楔块各方向尺寸示意
从图4可见,工件中只有一种波传播,这是由于在工件中声波的入射角大于第一临界角,工件中只有模式转换横波。提取图4各分图中声轴上声压随距离的变化曲线,取最远的极大值到声辐射面的距离为近场区长度,代入式(7)可求得近场区深度,并与式(6)和式(7)联合的计算结果进行比较,见表1和图5(相控阵超声探头5 MHz,16阵元,阵元间距0.6 mm,楔块倾角36.2°,自然偏转时楔块中声程12.3 mm)。
由表1和图5可见,理论计算和仿真结果一致,所以可用式(6)和式(7)计算线性相控阵超声探头偏转声场的近场区长度和近场区深度,以便指导工艺设计。

图4 不同折射角的声场仿真结果
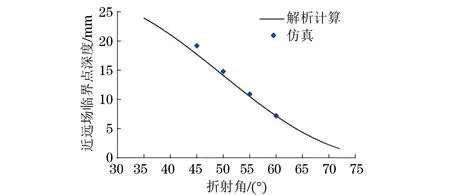
图5 相控阵偏转不同角度时近场区深度的理论计算和仿真结果对比

表1 不同偏转角度对应的近场区长度和近场区深度
3 结论
采用有效声辐射口径和几何声学的方法,计算了相控阵探头辐射偏转声场的近场区长度,研究了相控阵探头辐射声场的近场区深度随偏转角度变化的关系,理论计算与仿真结果吻合。结果发现探头越大,偏转角度越小,近场区长度越大,即可以采用聚焦声束检测的深度越大。
检测时,可以通过计算近场区长度来判断是否适合采用聚焦声场;也可以估计近场区深度,以判断现场偏转非聚焦声束检测中校准设备时,DAC曲线的合理性。即当DAC曲线的最大峰值点在近场区深度附近时,则一般认为DAC曲线合理,可以进行后续工作。否则,DAC曲线不合理,不能检测。
[1] SCHMERR W. Fundmentals of ultrasonic phased arrays[M]. New York:Springer, 2015.
[2] TUMSYS O, JASIUNIENE E. The focusing of the ultrasonic phased array in the case of non-contact NDE methods[J]. Elektronika ir Elektrotechnika, 2014, 20(3): 44-47.
[3] POTTER J N, CROXFORD A J, WILCOX P D. Nonlinear ultrasonic phased array imaging[J]. Physical Review Letters, 2014,113: 144301.
[4] PENG J, WANG L, ZHANG Y, et al. Study on the ultrasonic inspection method using the full matrix capture for the in service railway wheel[C]∥AIP Conference Proceedings. Baltimore, Maryland, USA: AIP 2014, 1581: 42-48.
[5] FAN C, PAN M, CHEN D, et al. Ultrasonic array time-reversal based super resolutionimaging[C]∥2014 IEEE Far East Forum on Nondestructive Evaluation/Testing (FENDT).Chengdu:IEEE:69-73.
[6] 彭小冲,费跃农. 相控阵超声接收动态聚焦算法及其物理实现[J]. 应用声学, 2014, 33(5): 15-23.
[7] 左延田,方雨, 刘晴岩,等. 角焊缝裂纹类缺陷相控阵超声检测工艺[J]. 无损检测, 2016, 38(6):6-9.
[8] 竺哲明, 黄伟勇,郭伟灿.聚乙烯管道热熔对接接头的超声相控阵检测[J]. 无损检测, 2017, 39(1):38-41.
[9] 周正干,李洋,周文彬.相控阵超声后处理成像技术研究,应用和发展[J].机械工程学报,2016,52(6):1-11.
[10] 薛利杰,刘晴岩,方雨,等.特种设备在役螺栓超声相控阵检测成像影响因素[J].无损检测,2016,38(7):6-10.
[11] 常俊杰,魏强,小倉幸夫,等.宽带高灵敏度柔性相控阵探头的发展与应用[J].无损检测,2016,38(6):24-27.
[12] 刘书宏, 郑晖,姜学平. 相控阵超声绝对声时法测量底面开口裂纹[J]. 声学技术, 2014,33: 331-335.
[13] 郑阳, 郑晖, 潘强华,等. 国外相控阵超声检测标准比较与分析[J]. 无损检测, 2016, 38(7): 56-65.
[14] GB/T 32563-2016 无损检测 超声检测 相控阵超声检测方法[S].
[15] 刘晓睿, 强天鹏,邬冠华. 加楔块超声相控阵的聚焦特性测试[J]. 无损检测, 2012, 34(11): 32-36.
[16] 孙芳, 曾周末, 王晓媛, 等. 界面条件下线型超声相控阵声场特性研究[J].物理学报,2011,60(9):94301.
[17] 张迪,吴先梅. 基于有限元的空耦超声相控阵Lamb波激发与检测[J]. 应用声学, 2015, 34(3):201-206.
[18] XU N, ZHOU Z. Numerical simulation and experiment for inspection of corner-shaped components using ultrasonic phased array[J]. NDT & E International, 2014, 63: 28-34.
[19] 姜学平,王鹏, 郑晖,等. 相控阵超声检测扇形扫描角度范围[J]. 无损检测, 2015, 37(11): 10-12.
[20] 姜学平, 王鹏, 韩庆邦,等. 带斜楔相控声束偏转聚焦延时特性研究[J].应用声学,2016,35(3):1-6.
[21] 米露,张德俊. 几种典型换能器声场特性的微机计算[J]. 声学技术, 1986, 5(3): 7-14.
[22] 涂春磊,邹建华,强天鹏,等.对接焊缝相控阵超声检测可靠性的CIVA仿真与试验[J]. 无损检测, 2013, 35(11): 22-26.
TheoreticalStudyonNear-FieldLengthofAcousticFieldforPhasedArrayUltrasonicTesting
JIANGXueping1,YUEYunfei2,ZHUANGFengdong3,MAOXiaohu2,ZHENGHui4,HANQingbang1
(1.CollegeofIOTEngineering,HohaiUniversity,Changzhou213022,China;2.SpecialEquipmentSafetySupervisionInspectionInstituteofJiangsuProvince,Changzhou213016,China;3.PetroChinaJinxiPetrochemicalCompanyMachineryFactory,Huludao125001,China;4.ChinaSpecialEquipmentInspectionInstitute,Beijing100013,China)
Phased array ultrasonic testing method is of flexible, reliable, efficient and suitable for industrial nondestructive testing. Near-field length was investigated for phased array ultrasonic testing homogeneous isotropic work pieces using oblique incident pulse shear wave. The theoretical calculations of near-field length and the simulations of the acoustic field for various deflection angles in phased array ultrasound inspections were carried out. It is shown that the near-field length decrease with increasing deflection angles when using general plexi-glass wedge of inclination angle being 36.2°. The conclusions of this paper can provide some reference for designing the testing procedure.
phased array ultrasonic testing; sector scan; near-field length; focusing acoustic wave
TG115.28
A
1000-6656(2017)10-0033-04
2017-02-09
国家自然科学基金资助项目(11604076,11574072,11274092);河海大学中央高校基金资助项目(2015B04714);江苏省特检院科技(科研)资助项目(KJ(Y)2016002)
姜学平(1983-),男,讲师,主要研究方向为超声检测
韩庆邦(1965-),男,教授,主要研究方向为超声检测,HQB0092@163.com
10.11973/wsjc201710008

