一种自适应的协同优化算法及其仿真

朱 枫，郑 松，葛文锋，葛 铭

(杭州电子科技大学自动化学院，浙江 杭州 310018)

一种自适应的协同优化算法及其仿真

朱 枫，郑 松，葛文锋，葛 铭

(杭州电子科技大学自动化学院，浙江 杭州 310018)

针对协同优化算法对初始点敏感，易收敛于局部最优值的问题，提出了一种自适应的协同优化算法.在系统级模型中，引入协同不一致性，改进动态松弛因子使优化设计点快速收敛于极值点；在学科级模型中，改造子学科目标，将一致性目标函数与子学科最大以动态的权重相加，考虑一致性同时又兼顾子学科独立性；采用二阶段优化过程，在迭代后期去除动态松弛因子与子学科最优目标函数，防止收敛过程震荡.仿真实验发现，自适应的协同优化算法对初始点不敏感，其优化效率得到了显著提升，且具有较强的鲁棒性.

协同优化；一致性；自适应

0 引 言

在现代工业场景中，工程控制复杂化的趋势已无可避免，应对庞杂问题的优化求解传统方法不再适用.对此，多学科综合优化设计(Multidisciplinary Design Optimization，MDO)[1]充分利用学科间的耦合关系，通过并行设计缩短了设计周期，已成为学术界的研究热点.1994年，Ilan K.等[2]首次提出了协同优化(Collaborative Optimization，CO)，CO算法将MDO问题分解为层次式的两级优化结构，各学科的优化过程有很强的自主性，可自主选择分析模型和优化算法[3-4].作为一种新兴优化算法，CO算法较传统优化算法在效率方面有很大的提高，但仍不够完善，比如：系统级模型中采用的一致性等式约束过强，缩小最优解搜索范围，甚至使可行域不存在[5]；优化结果对初始点的选取敏感，选取不当则易收敛于局部最优.为解决上述问题，文献[6]提出了松弛因子法，将系统级中的等式约束松弛为不等式约束，在此基础上，文献[7]利用学科间不一致性将松弛因子优化为动态松弛因子.文献[8]利用凝聚约束处理方法将系统级优化的多个等式约束凝聚成一个单约束，结合惩罚函数法将其转化为无约束优化问题.文献[9]引入自适应松弛因子的同时建立混合惩罚函数，提高了收敛效率.文献[10]利用系统级与学科级间的不一致性改进了系统级的自适应松弛因子.

上述方法集中于系统级模型的改进，虽然降低了一致性约束对全局收敛的负面影响，使算法的搜索域扩大而不易限于局部最优，但在学科级模型对于算法效率的贡献仍有待进一步深入研究.学科级模型仅仅是提供学科约束，未考虑与自身学科相关的子目标函数，缺乏对目标函数的寻优能力.为此，本文以提升学科级模型的寻优能力为目标，兼顾系统级与学科级模型两方面进行了改进，改进后的算法在迭代初期的优化效率与收敛速度上有了较大的提高.

1 标准CO算法

CO算法采用二层模型优化，分别构建了系统级与学科级模型.系统级模型负责消除学科间不一致性并在此基础上寻找整体最优解；学科级模型接收系统级传递来的目标，在保证各自约束的前提下，向系统级分配的期望值靠近.系统级和子学科级相互循环迭代，最终得到优化解.CO算法的表达形式如下[11]：

1)系统级模型

(1)

2)学科级模型

(2)

1.1 系统级模型的不足

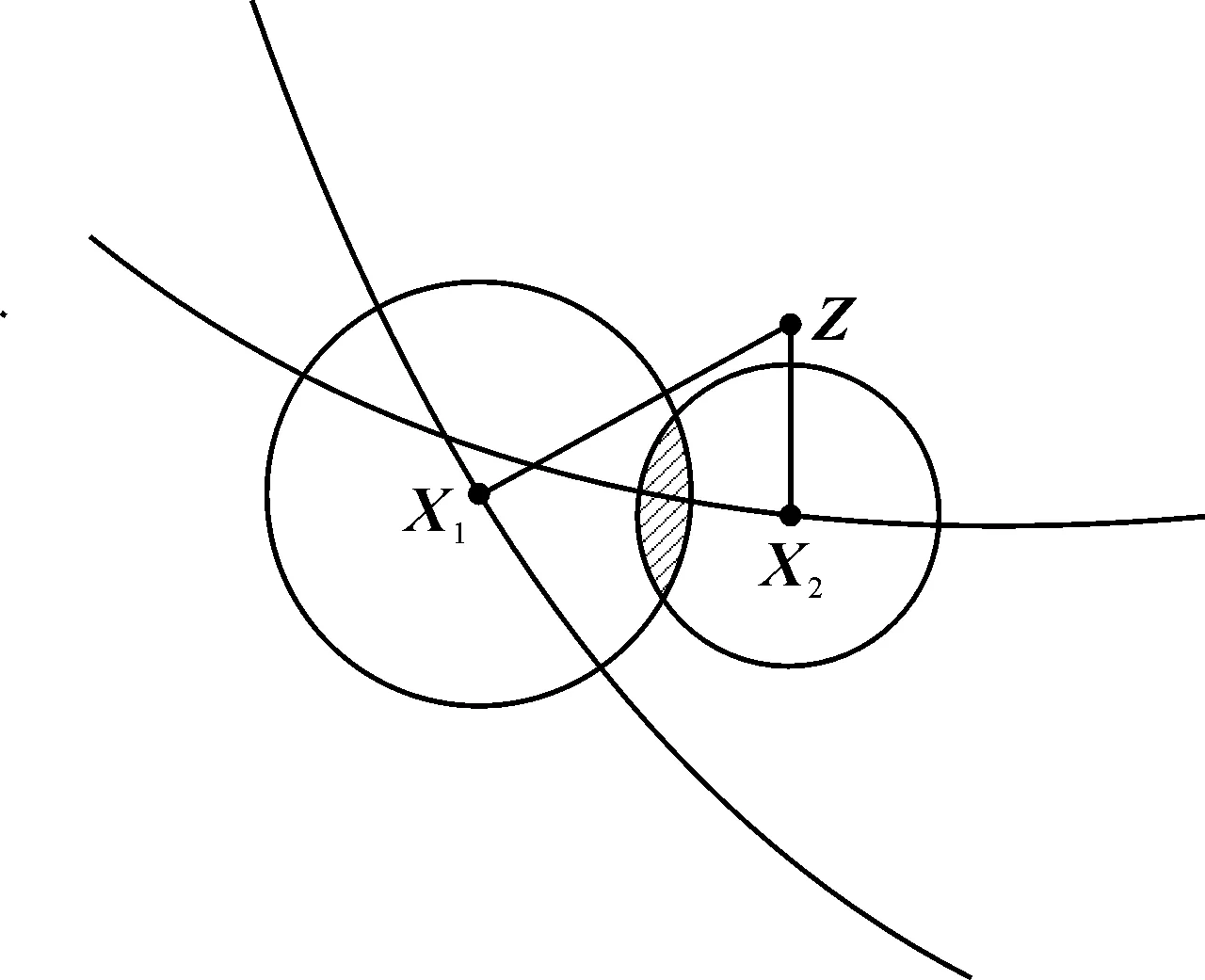
图1 松弛因子法几何解释

面对标准CO算法系统级优化可行域不存在问题，松弛因子法将系统级等式约束化为不等式约束：Ji≤εi.系统级优化的可行域变为以Xi为圆心εi为半径的高纬球交集.几何解释如图1所示.

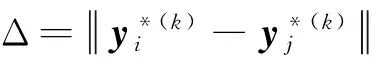
1.2 学科级模型的不足

标准CO算法将目标函数的优化全部放在系统级模型，学科级模型在每次迭代中的主要作用是提供学科约束，在优化方向上并未体现出原优化问题目标，缺乏对目标函数的寻优能力.同时，由于子学科最优设计点一直处于学科约束的边缘，当初值点远离约束边缘需要更多的迭代次数来拉近子学科最优点与系统级最优点，优化效率降低.

2 改进的SCO算法

针对系统级与学科级模型的不足，本文提出了一种自适应的协同优化算法(Self-adapting Collaborative Optimization, SCO)，并引入了协同不一致性因子.

2.1 协同不一致性因子

利用两次迭代间学科级与系统级优化所得最优点的距离大小，定义协同不一致性因子：

(3)

2.2 系统级模型的改进

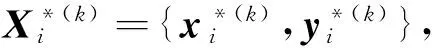
(4)

(5)

根据式(3)—(5)，构造松弛因子：

εi=(λid)2

(6)

2.3 学科级模型的改进

F=f1+f2+…+fn

(7)

系统级模型的目标函数F可以分解成i个子学科的子目标函数fi.为了充分利用学科级模型的优化能力，同时在优化方向上对系统级进行指导，将子目标函数按一定权重加入学科级模型的目标函数.改进后的学科级模型如下：

(8)

其中，ω1,ω2为自适应加权因子：

(9)

改进后的学科级模型在保留了一致性等式约束的基础上，利用自适应加权因子ω1,ω2动态加入了子学科目标函数fi.在迭代初期，对于一致性的要求较低，此时应较多的引入子学科的目标函数fi，学科级模型尽可能的寻找自己的理想值以此加快优化速度.当ρi不断减小，系统级最优点与学科级最优点的距离越来越短，此时应增加一致性目标函数的权重，确保学科级约束的作用.

2.4 二阶段优化过程

当迭代进入末期，寻优点进入各学科的交叉可行域导致学科间不一致性d为零，松弛因子εi亦为零对系统级优化不再起作用.而在学科级模型，由于系统级与学科级最优设计点的差距始终存在，fi的影响无法消除.学科级目标函数与系统级一致性等式约束的不一致阻碍了优化后期的收敛，优化过程出现震荡.

2.5 算法的实现步骤

算法的流程如下：

1)确定初始参数a，b，c；

4)设置初始点，并分配给子学科，子学科分别进行优化；

5)学科级模型将优化结果传递给系统级模型，系统级采用改进松弛因子εi进行优化；

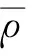
7)进入第二阶段的迭代，使用带松弛因子的标准CO算法继续优化直至满足收敛条件.

3 仿真案例

为测试SCO算法性能，本文对松弛CO算法(取松弛因子ε=10-4)和SCO算法进行对比，分别求解经典数值案例和齿轮减速器案例.本文算例均在MATLAB R2014b下的环境进行仿真计算，学科级和系统级优化均采用MATLAB非线性规划求解函数fmincon.

3.1 经典数值案例

经典数值案例数学模型如下：

(10)

通过SCO算法分解后得到系统级与学科级模型：

1)系统级模型

(11)

2)学科级模型

(12)

(13)

表1 经典数值案例下，优化结果比较

图2 各初始点在SCO算法下的迭代

分析表1可知，各初始点均能收敛于全局最优解附近.但是对于初始点1—4，采用松弛CO算法迭代次数非常高，运用SCO算法后迭代次数大幅下降，分别由原来的1 148次、986次、1 004次、1 069次下降至18次、19次、23次、21次.对于子学科理想点，在两种算法下均能快速收敛.

分析图2可知，运用SCO算法迭代曲线光滑，在迭代初期对目标函数保持了较大的前进速度，在迭代后期未出现震荡反复.SCO算法在经典数值算例真实可行，取得了良好的优化效果.

3.2 齿轮减速器案例

齿轮减速器优化案例是用来测试MDO优化设计方法性能的标准算例[12]，其特点是变量众多且包含了大量的约束条件.数学模型如下：

(14)

SCO算法求解需要对问题进行分解，按问题特征拆分为1个系统级和3个学科级.系统级及各学科的设计变量划分为：系统级设计变量Z={x1,x2,x3}，子学科1设计变量X1={x1,x2,x3}，子学科2设计变量X2={x1,x2,x3,x4,x6}，子学科3设计变量X3={x1,x2,x3,x5,x7}.各学科优化模型如下：

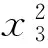
(15)

(16)

(17)

(18)

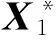
表2 减速器案例下，优化结果比较

图3 减速器案例下，各初始点在SCO算法下的迭代

对表2的数据进行分析可知，松弛CO算法对初始点较为敏感.其中初始点1由于距离全局最优点较远而陷入了局部最优，其余初始点虽然均可优化至全局最优点附近，但迭代速度差异明显.初始点2迭代次数达到1 104次，远高于初始点3与初始点4.

对比表2的优化结果，在改进算法下各初始点的收敛效率均有不同程度的提高.初始点1摆脱了局部最优且迭代次数减少为15次.初始点2初始点3初始点4的迭代次数大幅度下降，分别从松弛CO算法的1 104，469，647次减小至13，8，9次，各点之间差异较小.目标函数值与参考值2994.3548十分接近且约束最大值保持在一个较小的区间，说明优化结果与实际相符.通过以上分析可知，自适应协同优化算法较松弛CO算法对初始点不敏感，迭代效率得到大幅提升.

分析图3的收敛过程，在迭代初期目标函数值向全局最优方向快速靠近，这是由于子学科目标函数在优化方向上的指导作用加速了收敛速度.在迭代后期收敛曲线平滑并未出现震荡现象，说明二阶段优化模型起到了作用.

综上所述，自适应的协同优化算法高效可行，较松弛CO算法优化效率得到很大提升，具有一定的收敛性和鲁棒性.

4 结束语

本文针对标准CO算法尚存的缺点分别从系统级和学科级模型进行分析，并提出了与之对应的改进策略.在系统级模型中，采用改进的包含协同不一致性的动态松弛因子；在学科级模型中，改造子学科目标，将一致性目标函数与子学科最大以动态的权重相加，提升了对目标函数的寻优能力.同时采用二阶段优化过程解决了学科级目标函数与系统级约束不一致带来的负面影响.改进算法同时解决了系统级与学科级模型的不足，提高了自身的可行性和收敛速度，且对初始点不敏感.经典数值案例和齿轮减速器案例的优化结果表明，SCO算法对于不同初始点均可优化到全局最优点，且具有较好的鲁棒性，收敛速度较松弛CO算法有很大的提高.

[1] LEI G, LIU C, GUO Y, et al. Multidisciplinary Design Analysis and Optimization of a PM Transverse Flux Machine With Soft Magnetic Composite Core[J]. Magnetics, IEEE Transactions on, 2015,51(11):1-4.

[2] KROO I, ALTUS S, BRAUN R, et al. Multidisciplinary Optimization Methods for Aircraft Preliminary Design[J]. Proceedings of Aiaa/usaf/nasa/issmo Symposium on Multidisciplinary Analysis Ama Fl Aiaa, 1994：697-707.

[3] DARABI H, ROSHANIAN J, ZARE H. Design of liquid-propellant engine using collaborative optimization and evolutionary algorithms[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2014,229(2):232-242.

[4] 姚壮乐,陈超核.改进协同优化算法在船舶概念设计中的应用(英文)[J].船舶力学,2014(12):1453-1459.

[5] ALEXANDROV N M, LEWIS R M. Analytical and computational aspects of collaborative optimization for multidisciplinary design[J]. AIAA journal, 2002,40(2):301-309.

[6] ALEXANDROV N M, LEWIS R M．Analytical and computational aspects of collaborative optimization[EB/OL].(2002-12-13)[2016-01-12]．https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20000052922.pdf.

[7] 李响,李为吉.利用协同优化方法实现复杂系统分解并行设计优化[J].宇航学报,2004,25(3):300-304.

[8] 魏锋涛,宋俐,李言,等.改进的多学科协同优化方法[J].计算机集成制造系统,2013,19(9):2116-2122.

[9] 李冬琴,杨永祥,陈智同.一种改进的协同优化算法及其应用[J].计算机工程与科学,2013,35(1):137-141.

[10] 纪爱敏,殷旭.基于自适应松弛因子的协同优化方法[J].算机集成制造系统,2014,20(7):1530-1536.

[11] 朱崎峰,宋保维.一种快速收敛的多学科协同优化方法[J].计算机集成制造系统,2014,20(5):1013-1019.

[12] AZARM S, LI W C. Multi-Level Design Optimization Using Global Monotonicity.[J]. Journal of Mechanisms Transmissions & Automation in Design, 1989,111(2):259-263.

ASelf-adaptiveCollaborativeOptimizationandItsSimulation

ZHU Feng, ZHENG Song, GE Wenfeng, GE Ming

(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Collaborative optimization algorithms are sensitive to the choice of initial point and are prone to converge on a local optimum. A self-adaptive collaborative optimization algorithm is proposed with a view to overcoming such inconveniences. A collaborative non-uniformity is introduced at the system level to improve the dynamic slack factor such that the optimization design point converges rapidly on the extreme point. At the disciplinary level, the uniformity objective function and the sub-disciplinary optimal objective function are added up, by use of dynamic weightings, and the sum is treated as the sub-disciplinary objective function, hence giving allowance for uniformity as well as sub-discipline independence. A two-stage optimization process is utilized, and in the final phase of iteration, both the dynamic slack factor and the sub-disciplinary optimal objective function are removed to prevent excessive oscillation in the convergence process. A simulation was performed on classical cases, and the optimization results attested to the insensitivity of the proposed algorithm to the choice of initial point, its significant optimization efficiency improvement, and its good robustness.

collaborative optimization; uniformity; self-adaptation

TP301.6

A

1001-9146(2017)05-0061-07

2016-10-24

国家自然科学基金资助项目(61304211，61375078)

朱枫(1990-)，男，陕西铜川人，硕士研究生，协同优化生产调度.通信作者：郑松副教授，E-mail：zhs@hdu.edu.cn.

10.13954/j.cnki.hdu.2017.05.012