基于置信规则库推理的驻波液位仪误差补偿
李正辉,李 果,徐晓滨
(杭州电子科技大学自动化学院,浙江 杭州 310018)
基于置信规则库推理的驻波液位仪误差补偿
李正辉,李 果,徐晓滨
(杭州电子科技大学自动化学院,浙江 杭州 310018)
在基于声波共振原理的液位测量方法中,其测量误差通常是根据不同的液位测量高度进行分段补偿的,显然这种补偿不够精确.针对此问题,提出一种基于置信规则库推理(BRB)的测量误差补偿方法.由于不同液位高度下的测量误差大小与合成声波中的驻波个数、相邻驻波频率差的均值以及标准差等参数有密切关系,所以利用置信规则模型建立这些输入参数与输出补偿量之间的非线性关系.当在某一液位高度下获取输入参数值后,激活置信规则库中相对应的规则,运用证据推理(ER)算法融合被激活规则后项中的置信结构,在融合的结果中得出相应液位高度对应的误差补偿量,从而得到精确的测量结果.通过液位测量实验及分析说明,所提方法补偿后的测量结果的均方根误差为0.003 9,比利用分段补偿后的测量结果0.005 2更为精确.
置信规则库推理;声波共振;液位仪;测量误差补偿;报警监控
0 引 言
Denis D.等基于低频声波的共振原理,从初始共振频率(Resonance Frequency,RF)换算出液位高度[1].由于低频声波的波长较长避免了超声测距中寄生反射现象的发生,得到了较好的测量效果.但是,该方法的最大量程取决于初始RF,而该频率的最小值受扬声器原理、类型、声源体积和质量等因素的限制,一般仅为20 Hz[2].若在标准声速为331.45 m/s下进行测量,最大量程也只有8.28 m.并且,这也对麦克风的灵敏度提出了较高的要求,而一般麦克风可以感应到的最低音频为20 Hz左右,这些因素极大限制了该方法在长距离测量中的应用.针对此问题,文献[3]提出一种固定频段的声共振液位测量方法,首先将检测初始RF变为检测高于20 Hz的固定频段内出现的一组RF,利用相邻RF的等差关系,从驻波(共振频率波)公式中导出的RF液位换算公式得到多个测量值,将它们取平均后作为最终液位值,从而在一定程度上消除了观测噪声的影响,并将量程从原有的8.28 m扩展到10.00 m以上,满足了工业报警系统中对液位变量监测深度的要求.但是,由于一些客观原因的存在,使得测量结果仍然存在不确定性,由此引起的误差需要得到补偿,这些原因主要包括:驻波合成波公式及液位高度公式的近似推导和测量过程中扬声器、麦克风以及温度传感器造成的系统误差.为了补偿这些因素造成的误差,文献[3]采用了较为简单的分段补偿函数,将液位高度分为3段,各段中赋予一定的补偿值,该方法简单易行,但是无法精确刻画补偿值应有的变化.
由于引入误差的因素复杂且存在不确定,难以利用精确的模型对其建模,但是从大量的测量实验中总结得出:在不同液位高度下,误差的补偿量Δl和固定频段内的驻波个数M、相邻驻波频率差的平均值μ以及标准差V等参数存在复杂的非线性映射关系.而近几年发展的置信规则库(Belief Rule Based, BRB)推理方法,以其在模糊、不完整等主/客观信息处理中的优势,在非线性系统近似关系建模中得以广泛应用[4-5].本文基于多次测量实验中积累的经验,利用置信规则模型建立参数M,μ,V和Δl之间的非线性关系.当在某一液位高度下获取M,μ,V取值后,根据置信规则库中的规则与输入参数的相近程度会有选择性和不同程度的激活某些规则,然后再运用证据推理方法融合以上规则库中所激活的规则后项中的置信结构,在得到结果之后可得出相应液位高度对应的误差补偿量Δl,用其对测量值l进行补偿,获得更为精确的测量结果.最后,通过液位测量实验,说明经所提方法补偿后的测量结果比利用分段补偿后的测量结果更为精确.
1 声共振测距原理及液位仪物理结构
液位仪主要有6部分构成,分别为控制器、麦克风、通气管、导声管、温度计以及扬声器[4-5].文献[3]假设扬声器发出声波的频率随时间匀速变化,其频率范围可根据扬声器、麦克风等硬件性能以及最大液位高度hmax和死区dz范围选择,例如5 s内,从1 000 Hz~2 500 Hz进行线性扫频.
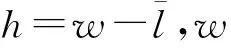
(1)
式中,M为在扫频频段中出现的驻波个数.由驻波公式可知,相邻2个驻波频率之差即为初始RF,由初始RF即可推导出一次l的取值,所以式(1)是将M-1次l的测量值取平均,其目的是为了消除观测误差的影响;声速c=331.45+0.6T,T为测量时刻的温度,f(k)(k=1,2,3…,M)为该扫频频段中出现的第k个共振频率,并有
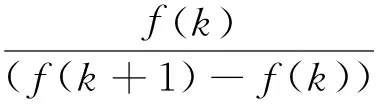
(2)
2 基于置信规则库推理的误差补偿方法
2.1BRB的系统结构
传统的IF-THEN规则与置信规则相比,其主要的区别在于置信规则的输出在前者的基础上融入了具有证据形式的置信分布,而且可以很好地建模在复杂决策问题上,比如不确定性信息的决策问题[7].本文运用BRB推理系统构建了参数M,μ,V和Δl之间的非线性模型.该系统参数关系及意义如表1所示.

表1 BRB误差补偿系统及输入输出量的意义
表1中,第k条规则表示为:
IF(e0,1isEk,1)∧(e0,2isEk,2)∧(e0,3isEk,3) THEN {(D1,βk,1),(D2,βk,2),…,(DN,βk,N)},
并有参数θk和δi,(k=1,2,…,L,i=1,2,3)
(3)
式中:∧为逻辑连接符,表示“与”的关系[5].
2.2 基于证据推理(ER)算法的BRB推理
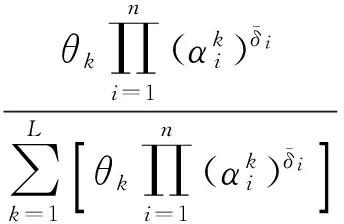
(4)
然后运用ER算法融合被输入参数激活的各个置信规则的后项信度结构,可以得到:
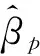
(5)
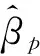
(6)
(7)
由式(5)估计输出值为:
(8)
3 实验测试
3.1 构建BRB规则库及确定输入与输出量的参考值
通过聚类方法结合专家经验对所获采集液位测量数据的分析,设置输入变量M,μ,V和输出变量Δl的参考值(语义值).M参考值(语义值)为A11=5(VS);A12=28(PS);A13=48(PM);A14=70(ML);A15=91(VL);μ参考值(语义值)为A21=16.38(VS);A22=23.11(PS);A23=50.23(ML);A24=278.95(VL);V的参考值(语义值)为A31=0.37(VS);A32=0.81(PS);A33=1.82(ML);A34=12.34(VL);Δl的参考值(语义值)为D1=-0.012(NS);D2=0.000(Z);D3=0.005(VS);D4=0.011(PS);D5=0.015(PM);D6=0.023(L);D7=0.025(VL).语义值VS,PS,PM,ML,VL,NS和Z分别代表“很小”、“一般小”、“正中”、“一般大”、“很大”、“负小”和“零”[8].置信规则库中的规则可以表示为:
Rk:IFMisEk,1ANDμisEk,2ANDVisEk,3,THEN Δlis{(D1,βk,1),…,(DN,βk,N)}
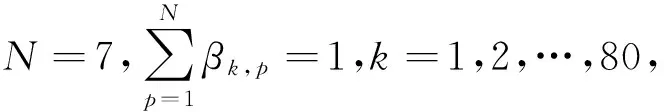
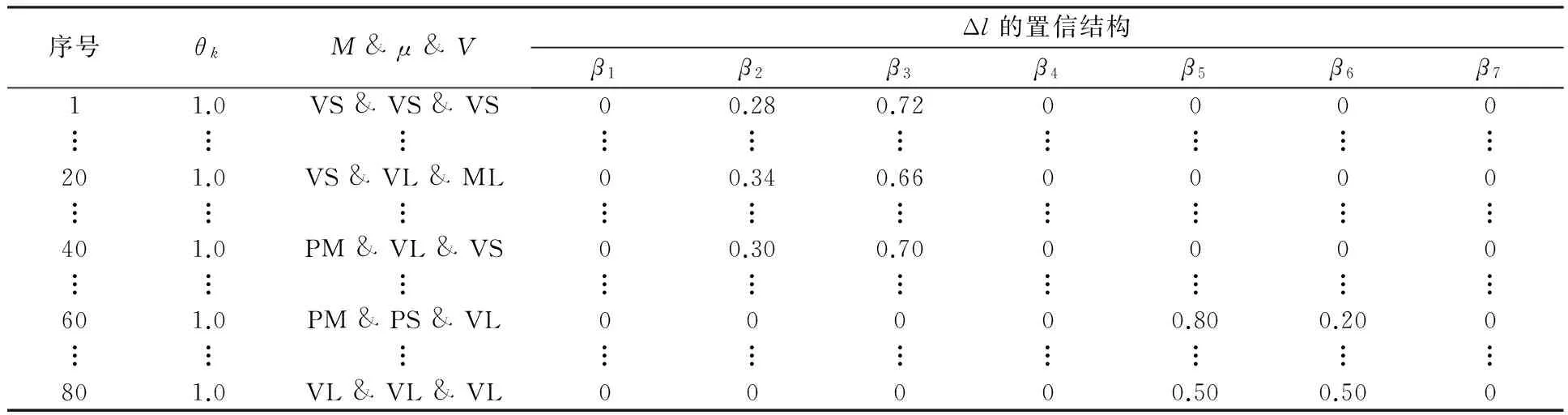
表2 BRB规则库部分参数取值
3.2 仿真结果对比

图1 BRB误差补偿与分段误差补偿的对比
为了验证BRB模型的效果,在0.6 m~10.8 m范围内采集42组测量数据,BRB推理模型的输入参数是每组中的M,μ,V,然后再运用证据推理(ER)算法,该模型的最终输出为误差补偿值.误差补偿曲线如图1所示.显然经过BRB系统的非线性拟合,相比文献[3]的分段补偿法,前者的估计值比后者更加趋近于真实补偿值.其均方根误差RMSE分别为分段补偿法0.005 2,BRB误差补偿法0.003 9,显然后者优于前者.
4 结束语
本文研究了基于置信规则库推理的音频共振液位仪误差补偿分析方法,描述了测量误差补偿与驻波的个数、相邻驻波频率差的均值及标准差3个参数之间的非线性映射关系.当系统可利用的高质量的测量数据足够多时,初始的专家系统即可利用这些参数进行进一步训练,提高了BRB系统的测量精度.下一步将利用更多的样本数据对所建立的BRB规则库参数进行优化.与神经网络等非线性系统建模方法相比,其可调参数物理意义的明确便于工程技术人员理解,不仅能使用客观样本数据,又能兼顾主观专家经验,更符合工程应用背景,方便工程人员参与BRB系统的建模过程.
[1] DONLAGIC D, ZAVRSNIK M, SIROTIC I. The use of one-dimensional acoustical gas resonator for fluid level measurements[J]. Instrumentation & Measurement,IEEE Transactions on, 2000,49(5):1095-1100.
[2] 赵辉,丁雷.利用声共振测量管件长度的研究[J].宇航计测技术,1998(6):1-7.
[3] 徐晓滨,赵晨萍,夏丙铎,等.基于固定频段声波共振原理的液位测量方法[J].计量学报,2011,32(1):53-57.
[4] XU D L, LIU J, YANG J B, et al. Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J]. Expert Systems with Applications, 2007,32(1):103-113.
[5] 徐晓滨,汪艳辉,文成林,等.基于置信规则库推理的轨道高低不平顺检测方法[J].铁道学报,2014,36(12):70-78.
[6] GEORGI H, ROELOFS L. The physics of waves[J]. Journal of the Acoustical Society of America, 1993,94(6):120-122.
[7] XU D L, LIU J, YANG J B, et al. Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J]. Expert Systems with Applications, 2007,32(1):103-113.
[8] 徐晓滨,李世宝,马雪,等.基于置信规则库的控制器及控制系统仿真[J].杭州电子科技大学学报,2016,36(3):78-83.
[9] CHEN Y W, YANG J B, XU D L, et al. On the inference and approximation properties of belief rule based systems[J]. Information Sciences, 2013,234(11):121-135.
MeasuringErrorCompensationofStandingWaveBasedLiquidLeverMeterUsingBeliefRuleBaseReasoning
LI Zhenghui, LI Guo, XU Xiaobin
(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
In acoustic resonance based liquid level measurement, the measurement error is compensated according to piecewise function of level heights. Obviously, this kind of compensation is not accurate enough. In order to deal with this problem, a new compensation method is presented based on the belief rule base(BRB). Because the measurement errors at different liquid level heights are closely related to the parameters such as the number of standing waves in the synthetic acoustic wave, the mean values and the standard deviations of the frequency difference between adjacent standing waves. The BRB can be used to model the complex nonlinear relationship between these parameters (inputs) and compensation value (output). When the values of the input parameters are obtained at a certain level height the belief rules activated by the inputs are combined by the evidential reasoning(ER) algorithm so as to obtain the fused belief structure about the compensation, and then, the accurate measurement results can be calculated from the fused result. Finally, the liquid level measurement experiment shows that the measured results after compensation by the proposed method are more accurate than those using the piecewise compensation method.
belief rule base reasoning; acoustic resonance; liquid level meter; measuring error compensation; alarm monitoring
TP274
A
1001-9146(2017)05-0057-04
10.13954/j.cnki.hdu.2017.05.011
2016-12-27
国家自然科学基金资助项目(61374123,61433001);浙江省公益性技术应用研究计划资助项目(2016C31071)
李正辉(1993-),男,河南许昌人,硕士研究生,信息融合与状态估计.通信作者:徐晓滨教授,E-mail:xuxiaobin1980@163.com.

