用“设点法”研究一道解析几何题
2017-11-01 17:25:23孟伟业
中学数学研究(江西) 2017年10期
陈 磊 孟伟业
扬州大学附属中学 (225000)
用“设点法”研究一道解析几何题
陈 磊 孟伟业
扬州大学附属中学 (225000)
文[1]对一道解析几何模拟试题进行了深度探寻,给出了一般性的命题:

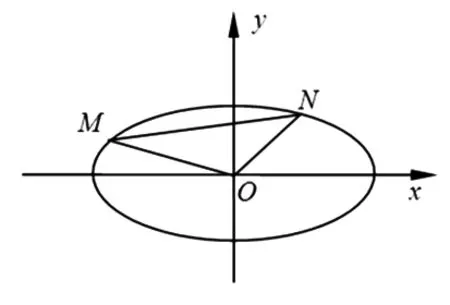
图1
文[1]中主要用的是“设线法”,即先设出直线方程,然后通过直线和曲线方程联立,进而使得问题解决的方法.而本文主要是用“设点法”对这一命题加以证明.所谓“设点法”,即假设曲线上的点的坐标,利用曲线方程的定义,将所设点代入曲线方程的一种方法.这一方法一般不需要直线与曲线联立.下面我们给出解析过程.在叙述过程中,我们对如何想、如何“推进”解题给出了一些说明.

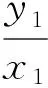
[考虑到椭圆的方程是平方的结构,故考虑将(*)式两边平方]



由上面的必要性和充分性,可知命题成立.
点评:在这一解法中,首先是将△MON的面积用M、N点的坐标表示,然后分析条件与目标的差异,充分利用好M、N点在椭圆上进行调整,将条件向目标转化,从而使得问题得以解决.
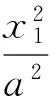


[1]苏立标.莫让浮云遮望眼 撩开雾纱见真颜——一道解析几何模拟试题的深度探寻[J].数学通讯(下半月),2016(8).
猜你喜欢
江苏教育(2021年54期)2021-08-31 10:12:32
中小学校长(2021年7期)2021-08-21 06:49:56
新农村(浙江)(2021年7期)2021-07-07 09:43:08
小学生作文(低年级适用)(2019年10期)2019-10-28 06:46:26
中国化肥信息(2019年2期)2019-04-04 05:53:30
数学教学通讯·高中版(2017年12期)2018-01-29 18:21:59
中华诗词(2017年4期)2017-11-10 02:19:03
数学学习与研究(2017年14期)2017-07-20 21:47:16
中学生英语·外语教学与研究(2017年3期)2017-05-19 23:18:46
知识经济·中国直销(2016年4期)2016-11-07 09:34:08

