数学解题，不妨“无中生有”

郭建华

江苏省南京市教育科学研究所 (210001) 刘权华江苏省南京市第二十九中学 (210036)

数学解题，不妨“无中生有”

郭建华

江苏省南京市教育科学研究所 (210001) 刘权华江苏省南京市第二十九中学 (210036)

如果把解题比作打仗，那么解题者的“兵力”就是数学基础知识，解题者的“兵器”就是数学基本思想方法，而调动数学基础知识、运用数学基本思想方法的数学解题策略就是“兵法”.“无中生有”是三十六计中第七种计策.其意思就是制造假相欺骗敌人，但又不是弄假到底，而是巧妙地由假变真，由虚变实，以假相掩盖真相，造成敌人的错觉.无中生有，这个“无”指的就是“假”，是“虚”.这个“有”指的是“真”，是“实”.无中生有就是真真假假，虚虚实实，真中有假，假中有真，虚实互变.

在数学解题中，有时看似“无”，其实是“有”，关键是要有一双“慧眼”.它对我数学解题的启示是：在解决某些问题时，要根据该问题的背景、结构特征，通过观察、比较、联想，恰当地构造出某个数学模型.所谓构造法，就是根据题设条件和结论的特殊性，构造出一些新的数学形式，并借助它认识与解决原问题的一种思想方法．应用好构造思想解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是弄清条件的本质特点和背景，以便重新进行逻辑组合．它的特点是：创造性使用已知条件，创造性地应用数学知识、数学模型等.下面结合例题，谈谈此法在数学解题中的运用.

1.充分地挖掘条件

分析:此题若是将其中的一个变量借助等式用另一个变量表示，再行运算，未尝不可，但是难度可想而知，若是充分地使用条件中的“1”，再利用书写规则(当一个式的系数是1或-1时，“1”通常省略不写)“无中生有”，立即就“柳暗花明”.

点评:但若是仔细观察，便会发现左边两个式子的分母有以下的关系，x+(1-x)=1，就可以使用无中生“1”的方法简便地予以证明了.本题中看似“无”，其实是“有”.关键是要充分的利用条件，挖掘条件，生出这个“有”来.

2.必要地巧用规则

(2)sin2α+sin2α+cos2α=sin2α+sin2α+cos2α-sin2α=2sinαcosα+cos2α

点评:在推导sin2α，cos2α和tan2α中用tanα表示的万能公式时，皆可以运用此法，效果确是恰到好处.

3.深刻地借用定义

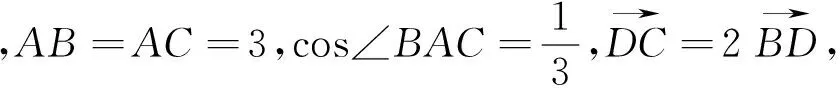
两组治疗前血液流变学指标比较，差异无统计学意义（P＞0.05），治疗后，观察组血沉、纤维蛋白原、红细胞压积、全血黏度、血浆黏度分别为（12.08±1.79）mm/h、（3.19±0.33）g/L、（0.43±0.05）L/L、（4.65±0.37）、（1.61±0.19），均低于对照组，差异有统计学意义（P＜0.05），见表1。

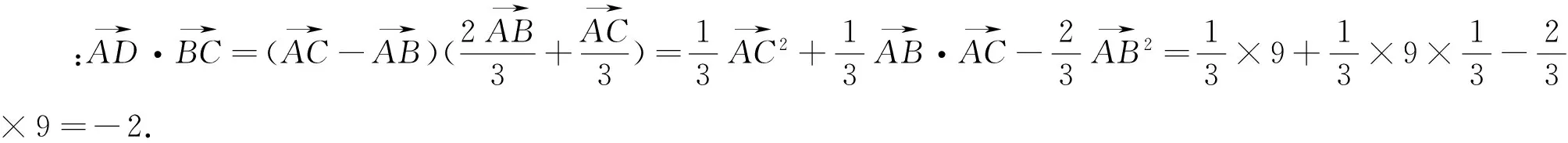
点评:此题，关键之处是对向量根据定义，巧妙拆分，无中生“A”，使得问题迅速解决.在定比分点的向量表示中，此法极为常用.此法就是利用充分向量减法的定义.此题中，由于AB=AC,故也可以由图，无中生“系”，通过建立直角坐标系，转化为对应的坐标，再用“代数法”求解，也很简单.

4.创造地利用模型

例4 6位身高不同的同学排成两排三列，若每列后面的同学均比他前面的同学高，则不同的排法有多少种？

点评:概率论是研究随机现象的一门数学分支，它既有独特的概念和方法，又与其它科学分支有着密切的联系，因此在解答有关数学问题时，如能根据题设条件构建概率模型，可使这些数学问题简洁巧妙地解决.

5.巧妙地使用规定

例5 4个0怎样能算出24？

解析:在阶乘(n!=1×2×3×…(n-1)×n，0!=1)的教学中，笔者带领同学们做游戏——算24点，“算24点”就是给一组数，通过一些数学运算(加、减、乘、除、乘方、括号)，使其结果等于24，每个数字都要用上，并且只能用一遍.比如给一组数2,3,4,6.一般有这样几种算法.法1：2×6+3×4=24；法2：(3-2)×4×6=24；法3：(6-3)×2×4=24.等.运算的范围一般在有理数范围内，最常见的方法就是构造24的因数3,8,4,6,2,12.

通过简单几个题目在他们小有成就而沾沾自喜的时候，我出了一道题：4个0怎样能算出24？足够的时间，激烈的讨论，学生们可谓绞尽脑汁，最后笔者给出了答案：(0！+0！+0！+0！)！=24，学生纷纷叹为观止，接着笔者点拨到：这就是“无中生有”，学生一下子群情激昂，雷鸣般的掌声经久不息，学习数学的情绪一下子就被调动起来.这似乎上升到“文化”的境界，这是我们多么渴望追求的一种高境界啊！然而，第二天一大早，有一个学生跑到笔者的办公室，急不可耐地告诉笔者，“老师，老师，我又有一种办法，“00∶00”就是24点呀……”内容如此的切合，学生如此的执著，一切都是那样的妙不可言.这样的故事，学生一生可能也难以忘怀.这样的过程似乎上升到一种更高的只可意会的境界.

6.巧妙地使用方程

例6 在平面直角坐标系xOy中，已知圆O1，圆O2均与x轴相切且圆心O1，O2与原点O共线，O1，O2两点的横坐标之积为6，设圆O1与圆O2相交于P，Q两点，直线l：2x-y-8=0，则点P与直线l上任意一点M之间的距离的最小值为_________.

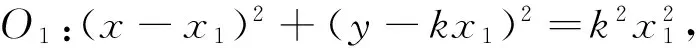
点评:根据已知条件与所求式子的特征，探寻问题的结构特征和数量关系，挖掘潜在已知与未知因素，从而联想有关的方程(或方程组)，利用方程理论求解，使问题在新的关系下转化，将陌生问题熟悉化，复杂问题简单化.

“无中生有”中的“有”，可以是数，可以是点，可以是图形，可以是坐标系，还可以是模型.这种方法，其实就是我们常说的“构造法”中的一种，构造法解题是一种创造性地思维过程，具有较大的灵活性和技巧性.在运用过程中，我们要仔细分析题目的结构特点，善于联想，应有目的，有意识地进行构造，始终“盯住”要“求”的目标.通过构造特殊数字、特殊规定(如0!=1)、特殊模型等将“未知轨道”中的问题转化为“常见可解的轨道”上来.