植被格局特征对大理河流域侵蚀产沙的响应

李斌斌，李占斌，郝仲勇，杨胜利，黄俊雄



植被格局特征对大理河流域侵蚀产沙的响应

李斌斌1,4，李占斌2※，郝仲勇1,3，杨胜利1,3，黄俊雄1

（1. 北京市水科学技术研究院，北京 100048；2. 西安理工大学西北水资源与环境生态教育部重点实验室，西安710048； 3. 北京市非常规水资源开发利用与节水工程技术研究中心，北京 100048；4. 北京林业大学水土保持学院，北京，100083）

为了进一步研究植被覆盖FBM（fractional brownian motion）分形维数在不同流域中对植被覆盖特征的综合效果及作为固定参数代替现有的植被量化指标在实际的水文、土壤侵蚀等预测模型中的应用，该文通过对大理河流域上中下游青阳岔、李家河和曹坪3个水文站控制流域的降雨、径流和产沙等资料的全面综合分析，以次降雨径流侵蚀功率作为侵蚀外营力输入，通过对站控流域地貌特征FBM分形维数、植被景观格局FBM分形维数和NDVI植被指数作为描述下垫面特征，以地理信息系统（GIS）为平台，利用GIS和RS技术，构建大理河流域侵蚀产沙量多元线性回归模型，并通过2组不同参数预测结果对比，结果表明：以植被格局分形维数为植被量化参数的模型输沙模数模拟值与实测值之间的相对误差和绝对误差比以NDVI为植被量化参数的小；在38场次暴雨洪水中，基于植被格局分形维数为植被量化参数的模型次暴雨输沙模数模拟值与实测值之间的相对误差小于10%、20%、50%的分别占总场次的34.21%、55.26%、86.85%；38场次暴雨输沙模数的模拟值和实测值之间的平均相对误差为25.19%，其中模拟值与实测值绝对误差小于300 t/km2有31场，植被格局FBM分形维数可以更好反映植被覆盖与水土流失之间的关系，并且分析得到植被格局分形维数与土壤侵蚀强度之间呈负相关关系，决定系数为0.506 6，即土壤侵蚀强度随着植被格局FBM分析维数的增大呈减小趋势，说明植被格局FBM分形维数对土壤侵蚀强度的影响较大。

植被；侵蚀；地理信息系统；分形理论；水土流失

0 引 言

植被是陆地生态系统的重要组成部分[1-3]，如何选择恰当的植被覆盖量化指标并能表达地表物质迁移过程中的植被作用、特别是筛选能全面准确地反映下垫面植被特征的植被覆盖参数是目前研究植被与地表物质迁移关系的重要问题[4-6]。分形理论被誉为“大自然的几何”[7-9]，目前分形理论大多集中在地形地貌特征量化等方面的研究[10-11]，将分形理论应用于植被格局空间分布特征分析的相关研究成果还很少[14-15]，特别是将分形理论深入到像元尺度上进行植被格局的分析研究更少[16-17]。目前基于NDVI植被格局与水土流失之间的关系，特别是对于流域植被格局分形维数与流域侵蚀产沙特征关系[18-20]，植被格局分形维数与土壤侵蚀强度之间的关系还未有相关的研究报道。

植被覆盖度是全球及区域气候数值模型中的重要参数，也是描述生态系统的重要基础数据。传统的植被覆盖度没有考虑植被空间的分布特征和内部异质性，不能完全表达植被的覆盖特征的复杂性。对植被覆盖数量进行特征量化的研究，从最初的植被覆盖度到大量基于遥感影像的植被指数都有大量的研究[21-22]，尤其是归一化植被指数（normalized difference vegetation index，NDVI）方面的研究，NDVI与植被盖度等量化植物生长状况的指标有很好的相关性，并且计算简单，是目前用来表征地表植被状况的重要指标[23-24]。水土流失是否严重可以通过植被覆盖度的高低间接反映和分析[25]；对于植被格局开展研究对于水土保持治理和规划有很大的指导和应用价值[26-28]。目前对NDVI植被指数进行地表植被覆盖度的量化研究相对较多[29]，NDVI植被指数是所选研究流域的一个平均值，仅用单一的NDVI值不能完全反映流域内各像元点的空间分布特征，也不能完全表达某一区域上的植被覆盖特征[30]。流域内植被覆盖FBM（fractional brownian motion）分形的标度的不变性特征是客观存在的，可以用FBM分维数来表述植被覆盖空间分布的复杂性。

本文以地理信息系统(GIS)为平台，开展了不同下垫面特征侵蚀产沙关系研究，构建以NDVI植被指数和植被格局分形维数作为量化参数的大理河流域次暴雨侵蚀产沙模型，对比分析植被格局FBM分形维数与NDVI植被指数在综合量化流域植被参数方面的优劣，为下垫面植被特征综合量化指标的筛选提供一种新的思路和方法。

1 研究区概况

大理河流域位于陕北毛乌素沙漠边缘，发源于靖边，干流全长170 km，流域面积3 906 km2，流域出口水文站为绥德站，集水面积3 893 km2。大理河流域地形地貌主要为丘陵沟壑区地貌和黄土梁峁丘陵沟壑地貌。大理河流域海拔900～1 700 m；属大陆性季风气候区；多年平均降水量439.8 mm，多年平均气温7.8～9.6 ℃；植被主要为干旱草原和落叶阔叶林的过渡带，植被覆盖度较低，植被空间分布不均匀。

大理河流域内共有水文站4个，分别为青阳岔站、李家河站、曹坪站和绥德站。其中青阳岔站以上主要为河源区，控制面积为662 km2，占绥德站以上控制面积的17%，多年平均来水量占绥德站以上来水量的17.4%，多年平均来沙量占12.4%。李家河站控制区以上为黄土丘陵沟壑区，控制面积807 km2，占绥德站以上控制面积的20.7%，多年平均来水量占绥德站以上来水量的18.9%，多年平均来沙量占16.5%。曹坪站控制面积187 km2，占绥德水以上控制面积的4.8%，多年平均来水量占绥德站以上来水量的5.1%，多年平均来沙量占3.5%。青阳岔站至绥德站之间为黄土峁状丘陵沟壑区。

2 流域侵蚀产沙量模型

本文结合前文研究成果，进一步探讨植被覆盖、植被格局与水土流失之间的关系以及植被格局分形维数在水文、土壤侵蚀等模型中的应用。研究选取了大理河上、中、下游的青阳岔、李家河和曹坪3个水文站控制流域为对象，分别选取降雨侵蚀因子(径流侵蚀功率)、地形地貌因子（地貌特征FBM分形维数）、植被覆盖因子（NDVI植被指数）和植被格局分形维数FBM，建立大理河流域降雨侵蚀产沙与地貌、植被、景观格局之间的耦合关系模型。探讨以降雨侵蚀因子、流域地貌特征FBM分形维数、均值化NDVI植被指数、植被格局FBM分形维数作为水土流失预报模型下垫面特征量化指标体系的可行性和实用性。

2.1 参数选取

2.1.1 径流侵蚀功率

本次研究将流域次暴雨洪水的径流深和洪峰流量模数的乘积QH作为表征次暴雨条件下天然降雨和流域下垫面对流域侵蚀产沙综合作用的指标，并令

式中为径流侵蚀功率，m4/(s×km2)，为径流深，mm，Q为洪峰流量模数，m3/(s×km2)。

径流侵蚀功率与径流深、洪峰流量和径流总量等径流特征单一量化指标相比，该指标对径流侵蚀力的刻画不仅更具综合性，而且从做功角度表达了其深刻的物理内涵。因此本文结合课题组研究成果，利用大理河流域青阳岔站、李家河站、曹坪站1990、1995、1999和2002年汛期实测的38场次暴雨洪水径流泥沙资料，根据鲁克新等[12-14]研究的径流径流侵蚀功率计算方法，计算得到的3个水文站38场次暴雨径流侵蚀功率，见表1。

表1 次暴雨降雨径流侵蚀功率计算结果

2.1.2 流域地貌特征FBM分形维数

不同的地形地貌特征，对流域侵蚀产沙的强度、方式和过程等具有重要影响，传统的流域地貌量化参数包括坡度、坡长、沟壑密度、流域高差、地形起伏度和土壤侵蚀面等。沈中原等[13]在其研究成果中，重点研究了流域地貌特征FBM分形维数与传统地形地貌相关参数的关系，通过研究表明地貌特征FBM分形维数可以综合量化指标来表征流域地貌特征，通过计算分别得到曹坪站、青阳岔站、李家河站以上流域的地貌特征FBM分形维数，3个控制站的地貌分形维数分别为2.495 3、2.476 5和2.489 1。具体计算结果见表2。

表2 各水文站控制流域地貌特征FBM分形维数计算结果

2.1.3 NDVI植被指数

作者在基于归一化植被指数的流域植被覆盖分形维数[10]中利用移动窗口法建立类似于数字高程数据组织结构的植被分布模型DVM。并且分别提取计算得到了各流域的NDVI值。

NDVI植被指数是植被生长状态以及植被空间分布密度的最佳指示因子，与植被分布密度呈线性相关。NDVI植被指数能较好的反映绿色植物生长状况和分布，可以宏观地反映地面绿色植物的生物量和覆盖度等植被定量特征。本研究采用各期遥感资料分辨率均为30 m× 30 m，时间均为每年的8～10月份。对遥感影像进行几何精度校正、大气效应纠正和角度效应纠正等预处理，分别以1990、1995、1999、2002年曹坪站、青阳岔站、李家河站控制断面以上流域的NDVI植被指数作为地表植被覆盖量化因子。由于1990年资料受云层的影响，其中青阳岔河、李家河的NDVI无法获取，具体NDVI植被指数统计表见表3。

表3 NDVI植被指数统计结果

2.1.4 植被格局FBM分形维数

像元NDVI值是计算流域植被覆盖FBM分形维数的依据，每个小流域内均值化NDVI是小流域植被覆盖总体状况的平均数量表达。利用李斌斌等[10-11]基于归一化植被指数的流域植被覆盖分形维数研究中建立的植被分布数字栅格模型，计算了曹格坪站、青阳岔站、李家河站控制断面以上各年的植被格局FBM分形维数，计算结果见表4。

表4 植被格局FBM分形维数计算结果

2.2 流域侵蚀产沙量模型构建

流域侵蚀产沙与下垫面关系密切，不同的下垫面、不同的植被格局对侵蚀产沙的作用也不同。本文结合3个水文站汛期径流侵蚀产沙过程资料，利用SPSS软件选取不同的参数进行多元线性回归对流域侵蚀产沙进行预测分析。探讨降雨侵蚀因子、地貌特征FBM分形维数、植被覆盖因子（NDVI植被指数）以及植被格局因子（植被格局FBM分形维数）对流域侵蚀产沙的作用。并将NDVI和植被格局分形维数作为参数分别与降雨侵蚀因子(径流侵蚀功率)、地形地貌因子相结合进行预测的结果与实测数据进行对比分析。

为了比较分析植被格局FBM分形维数和NDVI植被指数在表征植被覆盖综合量化指标方面的优劣。本研究共设置2组不同参数组合进行对比分析，第1组1选取降雨侵蚀因子(径流侵蚀功率)、地形地貌因子（地貌特征FBM分形维数）、植被覆盖因子（NDVI植被指数）作为预测流域侵蚀产沙的因子；第2组2选取降雨侵蚀因子(径流侵蚀功率)、地形地貌因子（地貌特征FBM分形维数）、植被格局分形维数FBM作为预测流域侵蚀产沙的因子。通过对模型各参数相关分析、模型计算结果汇总、系数的确定，利用SPSS软件构建流域次暴雨侵蚀产沙量多元线性回归模型，植被格局与降流域侵蚀产沙之间的耦合关系模型（1和2）如下：

3 结果与分析

3.1 植被格局分形维数与流域土壤侵蚀强度关系

在ArcGIS平台下，将大理河流域的DEM与2000年水利部水土保持监测中心公布的全国第二次遥感普查土壤侵蚀图（1∶10万）进行叠加，生成大理河流域土壤侵蚀强度图，详见图1。

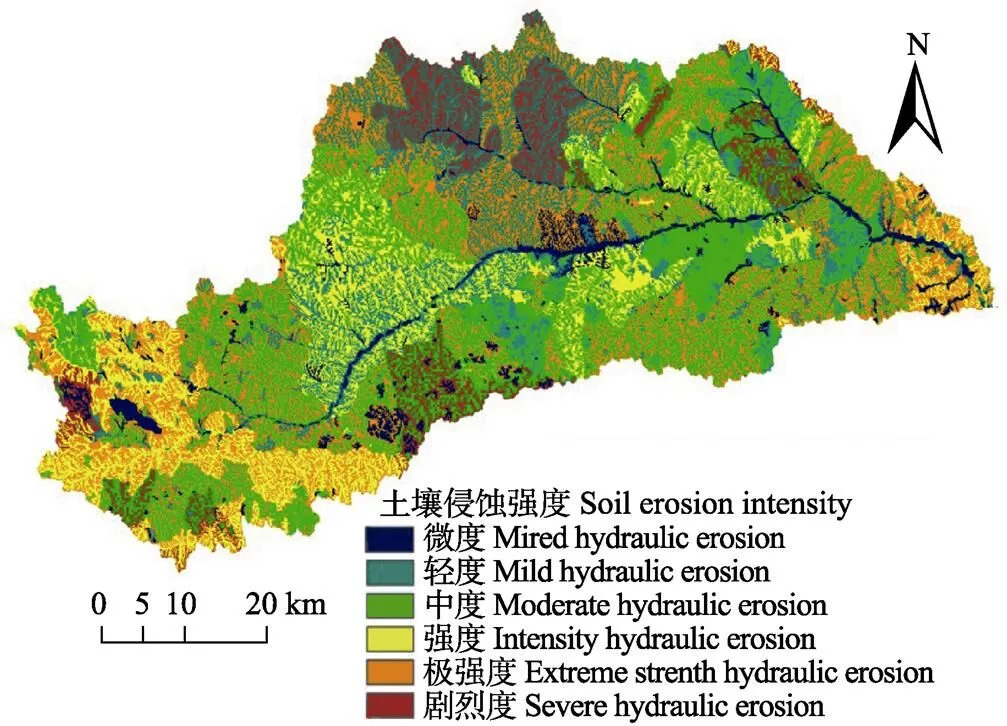
图1 大理河流域土壤侵蚀强度图

为了进一步定量研究大理河各级子流域侵蚀状况，本研究赋予各类侵蚀强度量化指标，对于微度侵蚀选取中间值500 t/km2×a，轻度、中度、强度和极强度选取区间平均数，剧烈侵蚀根据大理河以往研究成果取值为 20 000 t/km2×a，具体量化指标见表5。

表5 大理河流域侵蚀强度量化指标

利用侵蚀面积与侵蚀强度量化指标相乘累加求和，再除以各研究子流域面积，计算得到各研究子流域的土壤侵蚀强度量化值，利用植被格局布朗运动分形维数计算模型，分别计算得到大理河流域各子流域的植被格局FBM分形维数，在直角坐标系中点绘土壤侵蚀强度量化值与植被格局FBM分形维数之间的散点图，见图2。

从图2可以看出，植被格局FBM分形维数与土壤侵蚀模数之间存在着显著负相关，决定系数为0.506 6，即土壤侵蚀强度随着植被格局FBM分析维数的增大呈减小趋势，说明植被格局FBM分形维数对土壤侵蚀强度的影响较大。

植被覆盖度高相应的空间格局规整，植被格局分形维数越接近3，植被覆盖分布越均匀，产生的水土流失的危害越小，对应的土壤侵蚀强度也较小，土壤侵蚀强度随着植被格局FBM分析维数的增大呈减小趋势。因此植被格局分形维数也可以作为判断水土流失严重与否的参考指标。

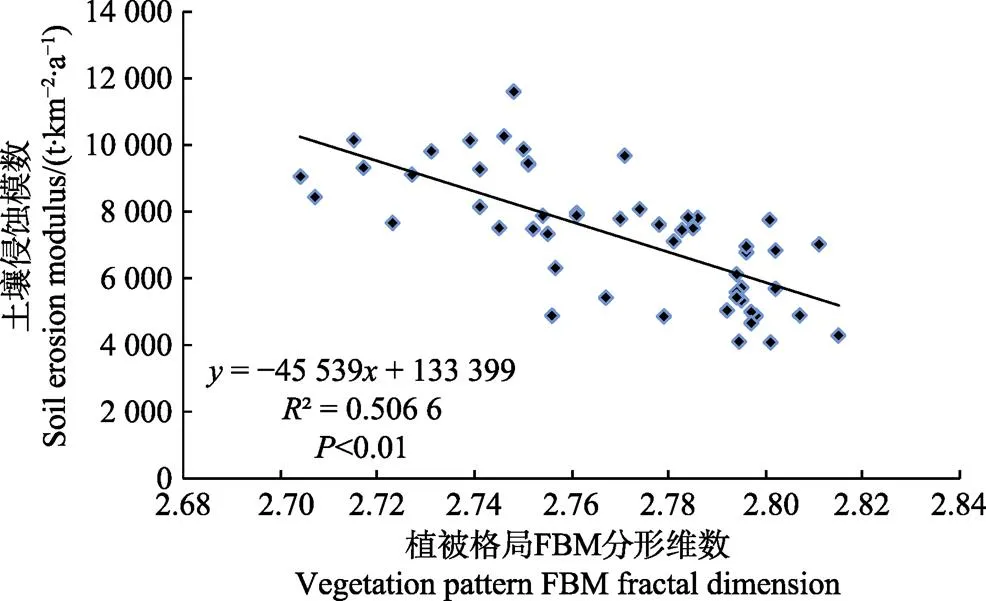
图2 植被格局FBM分形维数与土壤侵蚀强度关系图

3.2 大理河流域不同下垫面次降雨径流泥沙响应关系

利用不同计算参数分别构建的预测模型，分别针对不同组合进行预测计算，计算结果如图3所示。从图3中可以看出，以植被格局分形维数作为下面垫植被参数进行次暴雨输沙模数模拟计算结果和实测值吻合度更高。

图3 38场降雨输沙模数预测值与实际值的对比图

对2组计算模拟值分别与实测值进行相对误差分析，得到相对误差结果见图4，从图4a中可以看出，在38场次暴雨洪水中，基于以NDVI为植被参数的量化模型次暴雨输沙模数模拟值和实测值之间的相对误差小于10%的场次有8场，占总样本的21.0%；相对误差小于20%的场次共17场，占样本的44.73%；相对误差小于50%的场次共23场，占样本的60.53%；38场次暴雨输沙模数模拟值和实测值之间的平均相对误差为44.44%。

从图4b中可以看出，在38场次暴雨洪水中，以植被格局分形维数为植被量化参数的模型次暴雨输沙模数模拟值与实测值之间的相对误差小于10%的场次有13场，占总场次的34.21%；相对误差小于20%的场次共21场，占总场次的55.26%；相对误差小于50%的场次共32场，占总场次的86.85%；38场次暴雨输沙模数的模拟值和实测值之间的平均相对误差为25.19%。

从图4中可以看出，与NDVI为参数的模型的计算结果相比，以植被格局分形维数为植被量化参数的模型输沙模数模拟值与实测值之间的相对误差较小，即以降雨侵蚀因子(径流侵蚀功率)、地形地貌因子（地貌特征FBM分形维数）、植被格局FBM分形维数作为流域次暴雨侵蚀产沙模型因子的模拟值与实测值之间吻合度更好；基于植被格局分形维数为模型参数因子的输沙模数模拟值与实测值之间的相对误差随着输沙模数实测值的增大而减小。当输沙模数实测值小于500 t/km2时，模拟值与实测值之间的相对误差较大，另外相对误差随着输沙模数实测值的增大而减小。

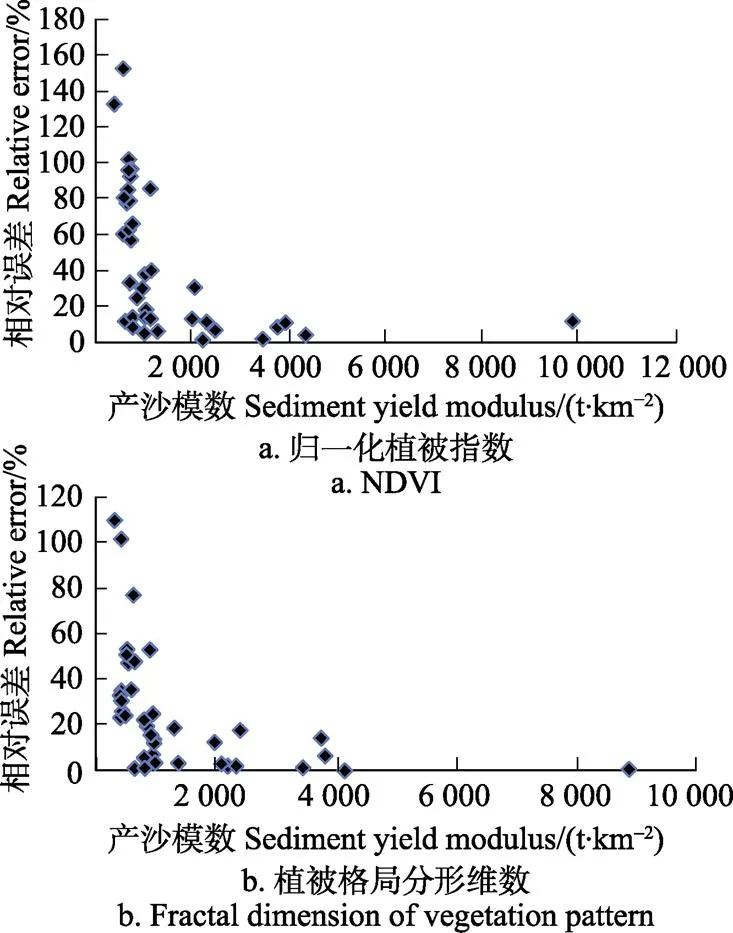
图4 两组模拟值与实测值的相对误差图

基于以NDVI为植被参数和植被格局分形维数为植被参数与径流侵蚀功率、地形地貌参数等所建立的模型次暴雨输沙模数模拟值与实测值之间的绝对误差结果见图5。从图5可以看出，基于植被格局分形维数表征植被覆盖量化参数的模型计算得到的大理河流域次暴雨输沙模数模拟值与实测值之间的绝对误差较小。

从图5a对于各场降雨的绝对误差而言，输沙模数大致介于0到2 000 t/km2之间的27场降雨的绝对误差值小于300 t/km有16场，降雨的绝对误差小于100 t/km2有6场，有12场降雨的绝对误差小于200 t/km2。在实际输沙模数大于2 000 t/km2之间的11场降雨中，有3场降雨的绝对误差大于600 t/km2，有8场降雨的绝对误差介于300～600 t/km2。

从图5b中可以看出，对于各场降雨的绝对误差而言，输沙模数大致介于0到2 000 t/km2之间的27场降雨的绝对误差值小于300 t/km2有24场，降雨的绝对误差小于100 t/km2有13场，有20场降雨的绝对误差小于200 t/km2。在实际输沙模数大于2 000 t/km2之间的11场降雨中，有1场降雨的绝对误差大于600 t/km2，有3场降雨的绝对误差介于300～600 t/km2，有7场降雨的绝对误差小于300 t/km2。

以植被格局FBM分形维数作为流域下垫面植被格局描述参数，构建降雨因子、地貌因子与植被格局与降雨侵蚀产沙之间的多元线型回归模型，模拟数值与实测数据绝对误差小于300 t/km2有31场，说明将植被格局分形维数作为下垫面植被综合量化参数是可行的，并且计算出来的结果是可靠的。

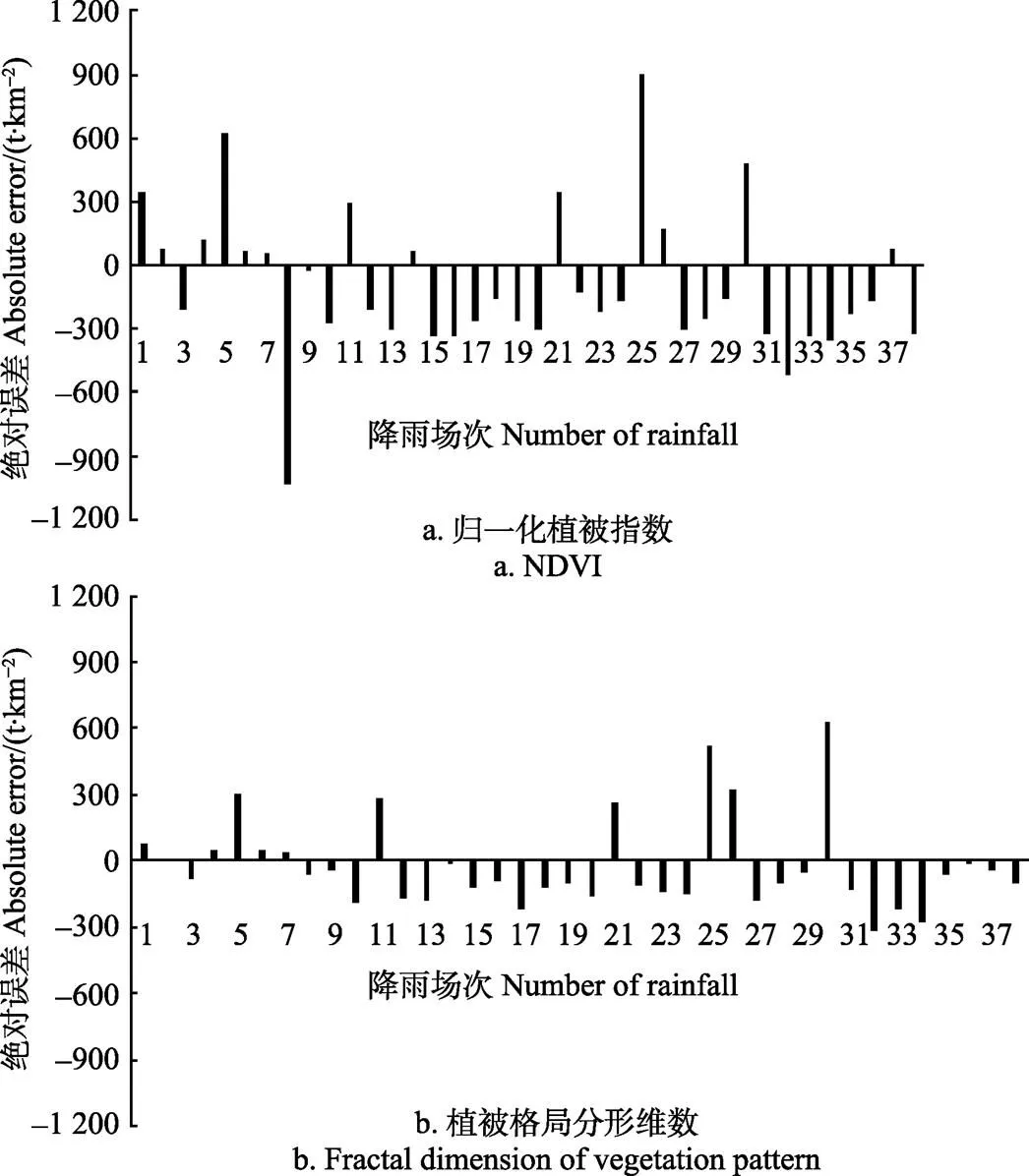
图5 大理河流域次暴雨输沙模数模拟值与实测值的绝对误差分析

通过上述对比，将植被格局FBM分形维数作为综合参数来预测流域次暴雨输沙模数的结果要优于以NDVI植被指数为参数的计算结果。

4 结论与讨论

分别以NDVI为植被参数和以植被格局分形维数为植被参数等建立的模型的决定系数分别为0.792、0.799，模型次暴雨输沙模数平均相对误差分别为44.44%、25.19%；土壤侵蚀强度随着植被格局FBM分析维数的增大呈减小趋势，植被格局FBM分形维数优于NDVI植被指数反映植被特征，与流域NDVI植被指数相比，植被格局FBM分形维数精度更高，更能全面准确地反映下垫面植被特征与流域水土流失之间的关系。

相比较传统的植被覆盖数量指标，植被格局分形维数作为植被量化指标综合不仅考虑了植被空间的分布特征和内部异质性，而且可以表征植被的覆盖特征的复杂性，以流域地貌特征FBM分形维数作为流域地貌特征综合量化指标，以植被格局FBM分形维数作为流域下垫面植被格局描述参数，反映流域综合下垫面指标对侵蚀产沙影响是合理和可行的；与降雨、径流和地形地貌等相关参数结合起来可以更全面表征流域下垫面特征，并且可以建立较完整的综合下垫面指标体系，为较高预报精度的黄土高原小流域侵蚀产沙预报模型奠定了科学理论依据。

本研究以大理河流域为例，考虑了流域地形地貌、降雨径流、植被格局等下垫面特征对侵蚀产沙影响，接下来将在更大范围尺度和其他流域对研究结果进行分析计算和应用。今后将进一步研究植被覆盖FBM分形维数在不同尺度、不同流域中作为植被量化参数在实际土壤侵蚀等预测模型中的应用。

[1] 郑江坤，李静苑，秦伟，等. 川北紫色土小流域植被建设的水土保持效应[J]. 农业工程学报，2017，33(2)：141－147. Zheng Jiangkun, Li Jingyuan, Qin Wei, et al. Effects of vegetation construction on soil and water conservation in small watershed of purplish soil region, northern Sichuan[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 141－147. (in Chinese with English abstract)

[2] 魏凤娟，李江风，刘艳中，等．湖北县域土地整治新增耕地的时空特征及其影响因素分析．农业工程学报[J], 2014, 14(30):267-276

Wei Fengjuan, Li Jiangfeng, Liu Yanzhong, et al. Spatial-temporal characteristics and impact factors of newly increased farmland by land consolidation in Hubei province at county level[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(14): 267－276. (in Chinese with English abstract)

[3] 许青云，杨贵军，龙慧灵，等. 基于MODIS NDVI多年时序数据的农作物种植识别[J]. 农业工程学报，2014，30(11)：134－144. Xu Qingyun, Yang Guijun, Long Huiling, et al. Crop information identification based on MODIS NDVI time- series data[J]. 2014, 30(11): 134－144. (in Chinese with English abstract)

[4] 刘琳，姚波. 基于NDVI象元二分法的植被覆盖变化监测. [J]. 农业工程学报，2010，26(13)：230－234. Liu Lin, Yao Bo, Monitoring vegetation–cover changes based on NDVI dimidiate pixel model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(13): 230－234. (in Chinese with English abstract)

[5] Surfleet C G, Skaugset A E, McDonnell J J. Uncertainty assessment of forest road modeling with the Distributed Hydrology Soil Vegetation Model[J]. Canadian Journal of Forest Research-Revue Canadienne De Recherche Forestiere, 2010, 40(7): 1397－1409.

[6] 杨闫君，占玉林，田庆久，等. 基于GF-1/WFVNDVI时间序列数据的作物分类[J]. 农业工程学报，2015，24(31)： 155－161. Yang Yanjun, Zhan Yulin, Tian Qingjiu, et al. Crop classification based on GF-1/WFVNDVI time series[J] Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 24(31): 155－161. (in Chinese with English abstract)

[7] 马克明，祖元刚. 植被格局的分形特征[J]. 植物生态学报，2000，24(1)：111－117. Ma Keming, Zu Yuangang. Fractal properties of vegetation pattern[J]. Acta Phytecological Sinica, 2000, 24(1): 111－117. (in Chinese with English abstract)

[8] 邹涛，漆德宁，张冬英，等. WorldView-1卫星植被全色图像分形维数的计算方法[J]. 计算机系统应用，2012，21(7)：222－224. Zou Tao, Qi Dening，Zhang Dongying，et al. Computing fractal dimension of the worldview-1 panchromatic vegetation image[J]. Computer Systems & Applications, 2012, 21(7): 222－224. (in Chinese with English abstract)

[9] 谢花林. 典型农牧交错区土地利用变化驱动力分析[J]. 农业工程学报，2008，24(10)：56－62. Xie Hualin. Driving force analysis of land use changes in the typical farming-pastoral ecotone[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(10): 56－62. (in Chinese with English abstract)

[10] 李斌斌，李占斌，宇涛，等. 基于归一化植被指数的流域植被覆盖分形维数研究[J]. 农业工程学报，2014，30(15)：239－247. Li Binbin, Li Zhanbin, Yu Tao, et al. Research on fractal dimension of vegetation cover based on normalized difference vegetation index in watershed scale[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(15): 239－247. (in Chinese with English abstract)

[11] 李斌斌，李占斌，李鹏. 基于GIS与RS的大理河流域植被格局分形维数时空变化特征[J]. 农业工程学报，2015，31(12)：173－178. Li Binbin, Li Zhanbin, Li Peng. Spatial and temporal variation characteristics of vegetation cover fractal dimension in Dali River watershed based on GIS and RS[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015,31(12): 173－178. (in Chinese with English abstract)

[12] 鲁克新，李占斌，鞠花. 径流侵蚀功率理论在不同尺度坡面侵蚀产沙中的应用[J]. 水资源与水工程学报，2009，20(4)：70－73. Lu Kexin, Li Zhanbin, Ju Hua. Application of runoff erosion power in the calculation of soil erosion and sediment yield on Hillslopes[J].Journal of Water Resources &Water Engineering 2009, 20(4): 70－73. (in Chinese with English abstract)

[13] 沈中原，李占斌，武金慧，等. 流域地貌形态分形布朗运动(FBM)分维数研究[J]，西安建筑科技大学学报（自然科学版），2007，39(5)：711－715. Shen Zhongyuan, Li Zhanbin, Wu Jinhui, et al. Research on the FBM characters of watershed topographic feature[J]. Journal of Xi¢an University of Architecture & Technology: Natural Science Edition, 2007, 39(5): 711－715. (in Chinese with English abstract)

[14] 张利，陈亚恒，门明新，等. 基于GIS 的区域生态连接度评价方法及应用[J]. 农业工程学报，2014，30(8)：218－226.Zhang Li, Chen Yaheng, Men Mingxin, et al. Assessing method for regional ecological connectivity and its applicationbased on GIS[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(8): 218－226. (in Chinese with English abstract)

[15] Deng Y, Chen X, Chuvieco E, et al. Multi-scale linkages between topographic attributes and vegetation indices in a mountainouslandscape[J]. Remote Sensing of Environment, 2007, 111, 122–134.

[16] Franklin J, Woodcock, Warbington R. Digital vegetation maps of forest lands in California: Integrating satellite imagery, GIS modeling, and field data in support of resource management[J]. Photogrammetric Engineering and Remote Sensing, 2000, 66, 1209－1217.

[17] 张宏鸣，杨勤科，李锐，等. 基于GIS和多流向算法的流域坡度与坡长估算[J]. 农业工程学报，2012，28(10)： 159－164. Zhang Hongming, Yang Qinke, Li Rui, et al. Estimation methods of slope gradient and slope length in watershed based on GIS and multiple flow direction algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(10): 159－164. (in Chinese with English abstract)

[18] 闫建梅，何联君，何丙辉，等. 川中丘陵区不同治理模式对土壤微团聚体分形特征的影响[J]. 中国生态农业学报，2014，22(11)：1294－1300. Yan Jianmei, He Lianjun, He Binghui, et al. Effects of different governance patterns of smallwatershed on fractal features of soil micro-aggregates in the hilly areas of central Sichuan Basin[J]. Journal of Chinese Ecological Agriculture, 2014, 22(11): 1294－1300. (in Chinese with English abstract)

[19] 颜亮，周广胜，张峰，等. 内蒙古荒漠草原植被盖度的空间异质性动态分析[J]. 生态学报，2012，32(13)：4017－4024.Yan Liang, Zhou Guangsheng, Zhang Feng, et al. Spatial heterogeneity of vegetation coverage and its temporal dynamics in desert steppe, Inner Mongolia[J]. Acta Ecologica Sinica, 2012, 32(13): 4017－4024. (in Chinese with English abstract)

[20] 付贵全，徐先英，徐梦莎，等. 民勤绿洲边缘2种生境红砂种群分形特征及影响因素[J]. 生态学报，2016，36(18)：5768－5776. Fu Guiquan, Xu Xianying, Xu MengSha, et al. A study of fractal properties of spatial distribution of Reaumuria soongorica population and its influencing factors in Minqin Oasis Fringe[J]. Acta Ecological Sinica. 2016, 36(18): 5768－5776. (in Chinese with English abstract)

[21] Hafzullah Aksoy, Erdem Unal, Sevket Cokgor, et al, Ebru Eris. A rainfall simulator for laboratory-scale assessment of rainfall-runoff-sediment transport processes over a two- dimensional flume[J]. Catena, 2012, 98: 63－72.

[22] Cuo L, Lettenmaier D P, Mattheussen B V, et al. Hydrologic prediction for urban watersheds with the Distributed Hydrology- Soil-Vegetation Model[J]. Hydrological Processes, 2008, 22 (21): 4205－4213.

[23] 沈中原. 黄土高原流域土壤侵蚀下垫面特征及其对水土流失的作用研究[D]. 西安：西安理工大学，2009.

Shen Zhongyuan. Study on the Characteristics of Soil Erosion Underlying Surface in Watershed and Its Effect on with Soil and Water Loss on Loess Plateau[D]. Xi’an :Xi’an University of Technology, 2009.

[24] 王正兴，刘闯，Huete Alfredo. 植被指数研究进展：从AVHRR-NDVI到MODIS-EVI[J]. 生态学报，2003，23(5)：979－987. Wang Zhengxing, Liu Chuang, Huete Alfredo. From AVHRR-NDVI to MODIS-EVI: Advances in vegetation index research[J]. Acta Ecologica sinica, 2003, 23(5): 979－987. (in Chinese with English abstract)

[25] Tucker C J. Red and photographic infrared linear combinations for monitoring vegetation[J]. Remote sensing of Environment, 1979, 8(2): 127－150.

[26] Barbosa H A, Huete A R, Baethgen W E. A 20-year study of NDVI variability over the northeast region of Brazil[J]. Journal of Arid Environments, 2006, 37(2): 288－307.

[27] 魏凤娟，李江风，刘艳中，等. 湖北县域土地整治新增耕地的时空特征及其影响因素分析[J]. 农业工程学报，2014，14(30)：267－276 Wei Fengjuan, Li Jiangfeng, Liu Yanzhong, et al. Spatial- temporal characteristics and impact factors of newly increased farmland by land consolidation in Hubei province at county level[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(14): 267－276. (in Chinese with English abstract)

[28] 张宏鸣，杨勤科，李锐，等. 基于GIS和多流向算法的流域坡度与坡长估算[J]. 农业工程学报，2012，28(10)： 159－164. Zhang Hongming, Yang Qinke, Li Rui, et al. Estimation methods of slope gradient and slope length in watershed based on GIS and multiple flow direction algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(10): 159－164. (in Chinese with English abstract)

[29] 许青云，杨贵军，龙慧灵，等. 基于MODIS NDVI多年时序数据的农作物种植识别[J]. 农业工程学报，2014，30(11)：134－144. Xu Qingyun, Yang Guijun, Long Huiling, et al. Crop information identification based on MODIS NDVI time- series data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(11): 134－144. (in Chinese with English abstract)

[30] 王海军，靳晓华，李海龙，等. 基于GIS和RS的中国西北NDVI变化特征及其与气候变化的耦合性[J]. 农业工程学报，2010，26(11)：194－203. Wang Haijun, Jin Xiaohua, Li Hailong, etal. NDVI variation and coupling analysis with climate change in northwest of China based on GIS and RS[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(11): 194－203. (in Chinese with English abstract)

李斌斌，李占斌，郝仲勇，杨胜利，黄俊雄.植被格局特征对大理河流域侵蚀产沙的响应[J]. 农业工程学报，2017，33(19)：171－178. doi：10.11975/j.issn.1002-6819.2017.19.022 http://www.tcsae.org

Li Binbin, Li Zhanbin, Hao Zhongyong, Yang Shengli, Huang Junxiong. Response of vegetation pattern characteristics to sediment yield in Dali River Basin[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 171－178. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.19.022 http://www.tcsae.org

Response of vegetation pattern characteristics to sediment yield in Dali River Basin

Li Binbin1,4, Li Zhanbin2※, Hao Zhongyong1,3, Yang Shengli1,3, Huang Junxiong1

(1.100048,; 2.710048,; 3.100048,; 4.100083,)

Landform, land cover and landscape pattern are important underlying surface conditions for basin erosion and the dominating factors for regional water and soil erosion. It is essential to study the law of water and soil loss in Loess Plateau area to find out how to quantize the features of basin underlying surface in a scientific and rational manner, establish a underlying surface indicator system suitable for describing the erosion environment of the Loess Plateau area, and study the interaction and coupling mechanism between various quantitative parameters and sediment generation arising from watershed erosion. By applying multi-disciplinary cross theory knowledge, combining GIS (geographic information system) and RS (remote sensing) technology, and taking Dalihe Watershed of Loess Plateau in north Shaanxi as the study area, this paper studied the relationship between the fractal dimension of vegetation distribution pattern and water and soil loss. The paper established a Brownian motion fractal dimension calculation model for the vegetation pattern of Dalihe Watershed based on NDVI (normalized difference vegetation index); the model illuminated the space distribution characteristics of NDVI of Dalihe Watershed. An erosion sediment yield model was also established for Dalihe Watershed, and the comparative study was performed on the advantages and disadvantages of the fractional Brownian motion (FBM) fractal dimension of vegetation pattern and the vegetation index NDVI in respect of comprehensive quantization of watershed vegetation parameters. The phase relation between fractal dimension of vegetation pattern and soil erosion intensity was analyzed, and the opinion that water and soil conservation for Dalihe Watershed should focus on small watersheds and the control measures thereof was proposed. In order to further study the general effects of FBM fractal dimension of vegetation coverage on vegetation coverage characteristics in different watersheds, and the application of fractal dimension in hydrology, soil erosion and other prediction models as a fixed parameter, substituting the existing quantitative indicator of vegetation, the paper established a multivariate linear regression model of erosion sediment yield for Dalihe Watershed through comprehensive analysis of the precipitation, runoff, sediment yield and other data of the watersheds monitored by such 3 hydrologic stations as Qingyangcha, Lijiahe and Caogeping, which are located at the upstream, middle reach and downstream of Dalihe Watershed respectively. The secondary rainfall runoff erosion power was set as the aggressive external force input, the FBM fractal dimension of geomorphologic characteristics in watershed controlled by station, the FBM fractal dimension of vegetation landscape pattern, and the vegetation index NDVI were used to describe the underlying surface features; the GIS was adopted as the platform, and the predicting outcomes of 2 groups of different parameters were compared and analyzed. The results show that: With fractal dimension of vegetation pattern as vegetation quantization parameter, both the relative error and absolute error between the simulation value of sediment transport module of the model and the measured value are smaller than that with NDVI as vegetation quantization parameter. Among 38 storm floods, 13 of them present that the relative error between the simulated value and measured value is lower than 10% with fractal dimension of vegetation pattern as vegetation quantization parameter in the rainstorm-sediment transport module of the model, accounting for 34.21% of the total; 21 of them present a relative error lower than 20%, accounting for 55.26% of the total; 32 of them present a relative error lower than 50%, accounting for 86.85% of the total; in the above 38 storm floods, the average relative error between the simulated value and measured value is 25.19%, including 31 storm floods showing an absolute error of lower than 300 t/km2between the simulated value and measured value. FBM fractal dimension of vegetation pattern can better reflect the relationship between vegetation coverage and water and soil loss. In addition, the analysis shows that fractal dimension of vegetation pattern presents a negative correlation with soil erosion intensity and the correlation coefficient is 0.506 6. It indicates that soil erosion intensity shows downtrend along with the increasing of FBM fractal dimension of vegetation pattern, which means that FBM fractal dimension of vegetation pattern significantly affects soil erosion intensity.

vegetation; erosion; geographic information system; fractal dimension; soil and water loss

10.11975/j.issn.1002-6819.2017.19.022

TP79; Q948

A

1002-6819(2017)-19-0171-08

2017-05-08

2017-08-22

科技部项目京津冀耗水管理与资源节水技术研发示范（2016YFC0401403）；北京市科技计划项目都市农业用水监测评价和管理平台研究与示范（D151100004115004）；国家自然科学基金“黄土高原生态建设的生态-水文过程响应机理研究”（41330858）；国家自然科学基金“基于能量过程的坡沟系统侵蚀产沙过程调控与模拟”（41471226）；北京市博士后工作经费资助项目

李斌斌，博士，主要从事水文水资源、土壤侵蚀与水土保持等方面的研究。Email：154223338@qq.com

※通信作者：李占斌，博士，研究员，博士生导师，主要从事水文水资源、土壤侵蚀与水土保持等方面的研究工作。Email：zbli@xaut.edu.cn