驳船横摇运动下波浪对沉管管段运动特性的影响

刘明，张俊，左卫广

（1.中交第一航务工程局有限公司，天津 300461；2.中交第四航务工程勘察设计院有限公司，广东 广州 510230；3.华北水利水电大学水利学院，河南 郑州 450045）

驳船横摇运动下波浪对沉管管段运动特性的影响

刘明1，张俊2，左卫广3

（1.中交第一航务工程局有限公司，天津 300461；2.中交第四航务工程勘察设计院有限公司，广东 广州 510230；3.华北水利水电大学水利学院，河南 郑州 450045）

沉管管段在沉放过程中，管段运动不仅受海面风、浪、流的影响，还受到驳船运动影响，属于复杂的水动力学问题。为探讨驳船运动对沉管管段运动的影响，假设驳船作强迫横摇运动，沉管管段运动由波浪作用下的沉管管段运动和驳船横摇运动引起的沉管管段运动两部分组成。建立波浪作用下的沉管运动时域模型，应用有限水深条件下的格林函数求解控制方程得到速度势。通过瞬时驳船横摇运动改变得到沉管管段运动新位移，在新位置计算速度势得到波浪力，带入沉管管段运动方程即可得到沉管运动。最后，探讨了不同工况下沉管管段的运动特性，并给出了相关结论。

驳船；沉管；横摇运动；横荡运动；低频运动

0 引言

自上世纪至本世纪70年代，国内外已建成的水下隧道达百座之多，而沉管隧道仅有40座。随着水力压接与压浆法等关键技术的解决，60余座沉管隧道就在1970—1995年的短短25 a间建成，尤其是在1990—1995年，修建了20座沉管隧道。随着沉管隧道越来越广泛的使用，对其的研究也越来越多，尤其是在管段接头防水、基础处理、沉管结构地震响应及抗震等方面[1-3]，但是对于管段沉放过程的研究相对较少。

张庆贺等[4]对管段沉放过程进行理论分析，与物理模型试验结果综合比较得到管段在沉放过程中的压载水重和水流力等参数。朱升[5]对浮运和沉放过程中沉管管段周围的流场和阻力特性进行了数值模拟与模型试验研究。肖龙飞等[6]通过物理模型试验对浙江宁波甬江沉管隧道进行研究，结果表明波流共同作用下，沉放吊缆最大张力大于定位缆张力，并且沉放吊缆及定位缆张力最大值随管段沉放深度的增加而变化不大。杨璨[7]研究了不同锚碇方式下沉管管段运动响应，并给出了最优的布缆方式，探讨了锚碇缆的重度、刚度和材料的变化对沉管管段运动响应的影响。

沉管管段沉放过程中，管段运动不仅受海面风、浪、流的影响，还受到驳船运动影响，属于复杂的水动力学问题。本文针对复杂荷载进行简化，仅探讨在波浪条件下，驳船作强迫横摇运动下沉管管段的运动特性。

1 波浪作用下沉管运动数学模型

沉管管段沉放属于大尺度结构物与流体相互作用的问题，忽略黏性，可采用势流理论进行分析[8-9]，用势流理论求解波浪与结构物的相互作用问题可归结为求解Laplace方程的定解问题。在实际工程中，当缆绳与沉管组成的沉放运动体系为非线性体系时，沉管管段运动不再是简谐运动；同时，沉放系统的缆绳受力-变形关系呈非线性关系，故不能使用解析方法和数值模拟中的频域方法。本文采用边界元方法建立沉管管段运动的时域数学模型，应用有限水深条件下复杂格林函数进行求解控制方程得到速度势，通过波浪力计算公式得到波浪力，最后求解沉管管段运动方程即可得到沉管管段的运动，其详细推导余求解参考陈智杰的研究[10]。

2 考虑驳船纵摇运动下沉管运动数学模型

假定驳船在横摇方向做强迫简谐运动，其横摇运动方程采用如下表达式：

式中：b为驳船做横摇运动的振幅；ω为入射波频率；θ为驳船运动与波浪之间的相位差；t为时间变量；TR为缓冲周期。

当驳船作强迫横摇运动时，忽略沉管运动对驳船运动的影响，仅考虑驳船横摇运动对沉管运动的影响，认为沉管横摇方向与驳船具有相同的

位移变化。 t时刻驳船的横摇角度为R（t），沉管位置为ξj（t）（j=1，2，3，4，5，6）。t+Δt时刻驳船位置R（t+Δt），仅考虑驳船横摇运动影响时沉管瞬时位置ξRj（t+Δt）为：

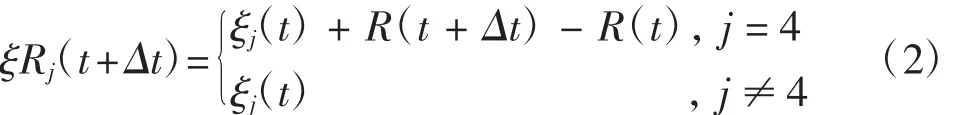
在t时刻，驳船横摇运动使沉管位置由ξj（t）变成ξRj（t+Δt），数值求解对应于沉管位置ξRj（t+Δt）的速度势φS和波浪力Fk′。然后把ξRj（t+Δt）和Fk′代入沉管运动方程，即可得到t+Δt时刻考虑波浪与驳船横摇运动共同影响的沉管位置ξj（t+Δt）。

3 算例计算及分析

数值计算中，沉管长×宽×高为100 m×15 m×10 m。波浪为规则波，周期T为5 s，波高为1.0 m。钢缆绳直径0.3 m，弹性系数为2.75×106kg/cm2。驳船横摇运动振幅与相位见表1。

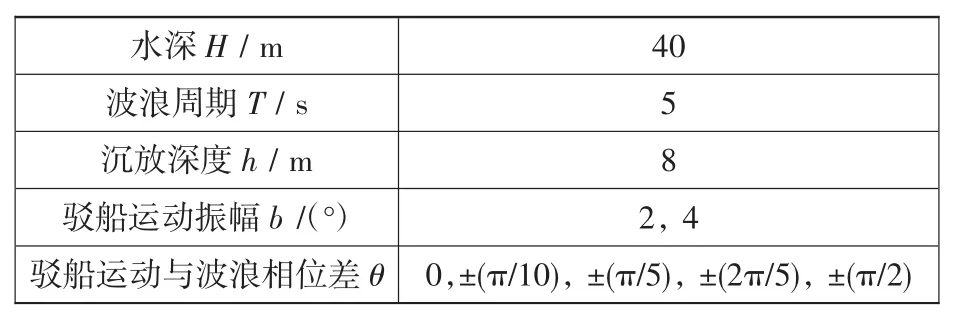
表1 计算工况Table 1 Working condition of calculation

图1给出了忽略驳船横摇运动情形下沉管横摇运动时间过程线与入射波浪的时间过程线的比较。由图1可见，沉管横摇运动过程线与入射波浪过程线相比，两者同步，即入射波浪与忽略驳船运动的沉管横摇运动之间的相位差为0。此时，沉管横摇运动幅值约为0.4°。

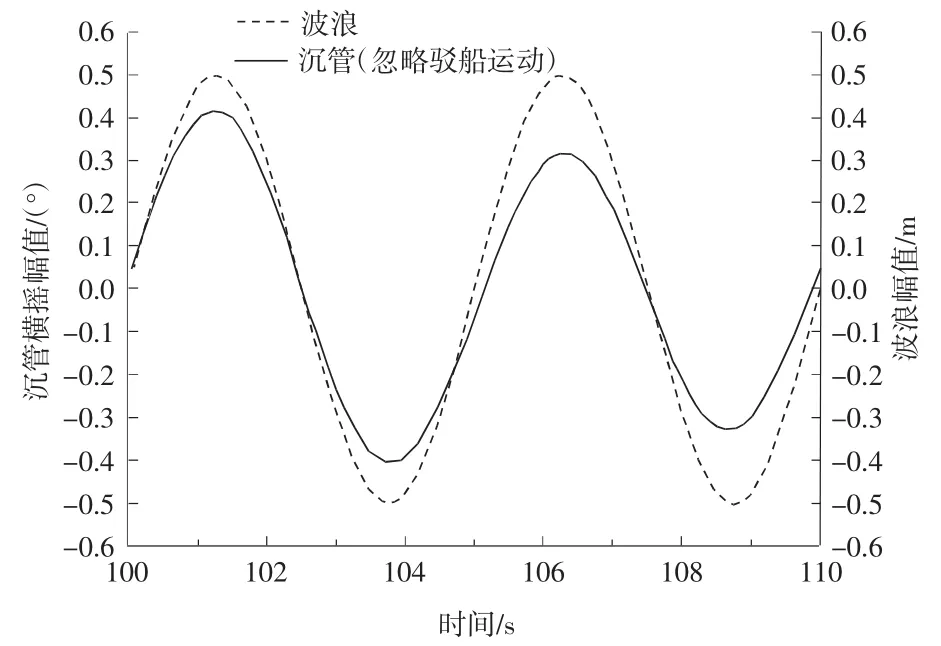
图1 忽略驳船运动的沉管横摇运动时间过程线Fig.1 Time history of rolling motion of the tunnel element without the barge motion

图2是驳船横摇运动振幅为4°、相位分别为-π/2，0和+π/2情形，考虑波浪作用和驳船横摇运动共同影响的沉管运动响应分量与忽略驳船运动时的沉管运动响应分量的比较。

图2 驳船横摇与忽略驳船运动的沉管运动响应（b=4°）Fig.2 The motion response of the tunnel element with and without the barge rolling motion(b=4°)

由图2可见，考虑驳船横摇运动时的沉管横摇运动响应与忽略驳船运动时的沉管横摇运动响应相比，在运动幅值与相位上都发生较大的变化。当驳船横摇运动幅值为4°时，驳船横摇运动与波浪不同相位情况下的沉管横摇运动幅值均远远大于忽略驳船运动的沉管横摇运动幅值。同时，考虑驳船横摇运动的沉管横摇运动过程线也与忽略驳船运动的沉管横摇运动过程线存在相位变化。

对于横荡方向运动来说，与忽略驳船运动的沉管横荡方向运动相比，考虑驳船横摇运动的沉管横荡运动包括两种运动，一种是与波浪频率相同的运动，称为波频运动，另外一种运动频率要远小于波浪频率，称为低频运动。

从图2中可知，考虑驳船横摇运动的沉管横荡波频运动幅值与忽略驳船运动的沉管横荡波频运动幅值相差不大，可以认为驳船横摇运动对沉管横荡波频运动没有影响。而对于低频运动来说，考虑驳船横摇运动的沉管横荡低频运动幅值要远大于忽略驳船运动的沉管横荡低频运动幅值，说明驳船横摇对沉管横荡低频运动影响很大。在升沉方向，考虑驳船横摇运动的沉管升沉运动过程线与忽略驳船运动的沉管升沉运动过程线几乎重合，说明驳船横摇运动对沉管升沉运动没有影响。

图2的历时曲线表明，考虑驳船横摇运动的沉管横荡运动包括低频运动和波频运动，忽略驳船运动的沉管横荡运动只有波频运动，且考虑驳船运动和忽略驳船运动两种情况下的沉管横荡波频运动幅值相同，即驳船横摇运动仅对沉管横荡低频运动有影响。因此，考虑驳船横摇运动的沉管横荡运动减去忽略驳船运动的沉管横荡运动，即可得到考虑驳船横摇运动的沉管横荡低频运动过程线。

为探讨驳船横摇运动与波浪运动之间相位差对沉管横摇运动的影响，图3给出了驳船横摇运动幅值为4°、驳船横摇运动与波浪之间的相位差分别取-π/2，-π/5，+π/5和+π/2情形的沉管横摇运动过程线。

图3中虚线表示忽略驳船运动的沉管横摇运动过程线，点画线表示驳船横摇运动过程线，直线表示考虑驳船横摇运动幅值和相位的沉管横摇运动过程线。对于沉管横摇方向运动，当驳船具有不同相位时，沉管管段横摇方向相差不大。结合图2可得，由于忽略驳船运动时沉管管段横摇方向运动仅为0.4°，而图3中驳船横摇振幅为4°，两者相差较大，驳船做横摇运动对沉管管段横摇方向的影响要远大于波浪影响。因此，当驳船横摇振幅一定时，驳船相位的改变对沉管管段横摇方向运动影响不明显。

图3 驳船横摇运动下沉管横摇运动过程线（b=4°）Fig.3 Time history of the tunnel element in the swaying motion under the barge swaying motion（b=4°）

图4中给出了驳船横摇运动幅值为4°、驳船横摇运动与波浪之间的相位差分别取-π/2，-π/5，+π/5和+π/2情形的沉管横荡低频运动过程线。

从图4中可以看出，当驳船与波浪之间的相位差为-π/2和π/2时，沉管横荡低频运动分别达到负向和正向最大位移，沉管横荡低频幅值分别为-0.63 m和0.62 m。当驳船与波浪之间的相位差为-π/5和π/5时，沉管横荡低频幅值分别为-0.34 m和0.42 m。由此可见，随着驳船与波浪相位差的增加，沉管横荡低频运动幅值也相应增加。同时，图4中明显可见不同相位的沉管横荡低频运动周期相同，均为60 s。说明沉管横荡低频运动周期与驳船横摇运动无关，可能与沉管管段沉放深度有关。

图4 驳船横摇运动下沉管横荡低频运动过程线（b=4°）Fig.4 Time history of the low frequency motion of the tunnel element in the sway direction under the barge swaying motion（b=4°）

图5中给出了驳船横摇运动振幅b=2°～4°、相位θ=-π/2～π/2情形对应的沉管横荡低频运动幅值。

图5 驳船横摇运动下沉管横荡运动幅值（H=1.0 m，T=5 s）Fig.5 Movement amplitude of the tunnel element in the swaying motion under the barge swaying motion（H=1.0 m，T=5 s）

从图5可以看出，当驳船横摇θ一定时，沉管横荡低频运动幅值随驳船振幅的增加而增加。当驳船横摇运动与波浪之间的相位差为-π/2时，沉管横荡方向运动达到负向最大。随着相位差的逐渐减小，沉管横荡低频运动幅值也相应减小，当驳船横摇运动与波浪之间的相位差为0时，沉管横荡低频运动幅值最小。随着相位差的进一步加大，沉管横荡方向正向位移逐渐加大，当驳船横摇运动与波浪之间的相位差为π/2时，沉管横荡低频运动幅值达到正向最大。

4 结语

本文研究了考虑驳船横摇运动与波浪联合作用下的沉管运动特性。研究发现：

1）当驳船横摇相位θ一定时，沉管横摇方向运动幅值随着驳船横摇振幅的增加而增加。而当驳船振幅一定时，驳船与波浪之间的相位差对沉管横摇方向运动影响较小。

2）驳船横摇运动对沉管横荡低频运动有较大影响。驳船横摇运动相位差为-π/2和+π/2时，沉管横荡方向运动分别达到负向和正向最大位移。驳船横摇运动对沉管横荡波频运动无影响。

沉管管段沉放是一个复杂的水动力学问题。沉管管段和水面驳船不仅同时受到波浪作用，而且两者之间由于缆绳连接也互为影响，属于波浪场中的耦合问题，将在下一步工作中进行深入的研究。

[1]ANASTASOPOULOS I,GEROLYMOS N,DROSOS V,et al.Nonlinear response of deep immersed tunnel to strong seismic shaking[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(9):1 067-1 090.

[2] DING Jun-hong,JIN Xian-long,GUO Yi-zhi,et al.Numerical simulation for large-scale seismic response analysis of immersed tunnel[J].Engineering Structures,2006,28(10):1 367-1 377.

[3] HASHASH Y M A,TSENG W S,KRIMOTAT A.Seismic soilstructure interaction analysis for immersed tube tunnels retrofit[J].Geotechnical Special Publication,1998,2(75):1 380-1 391.

[4]张庆贺.沉管隧道浮运与沉放阶段受力性态研究[D].上海：同济大学，2004.ZHANG Qing-he.Research of loading behavior of floating and surveying of immersed tube[D].Shanghai：Tongji University,2004.

[5]朱升.沉管隧道管段浮运和沉放过程中流场和阻力特性的研究[D].北京：北京交通大学，2009.ZHU Sheng.Flow field and resistance property of the pipe section of tube tunnel in the process of tugging and immersing[D].Beijing:Beijing Jiaotong University,2009.

[6] XIAO Long-fei,YANG Jian-min.Experimental study on mooring,towing and installing of immersed tunnel caissons[J].Shanghai Jiaotong University:Science,2010,5(1):103-107.

[7] 杨璨.锚碇沉管管段沉放运动的水动力数值研究[D].大连：大连理工大学，2013.YANG Can.A hydrodynamic numerical study on the immersion motion of tunnel element with mooring lines[D].Dalian:Dalian University of Technology.2013.

[8] HESS J L,SMITH A M O.Calculation of non-lifting potential flow about arbitrary three-dimensional bodies[J].Journal of Ship Research,1964,8(2):22-44.

[9]TENGB,TAYLORRE.Newhigher-orderboundaryelement methods for wave diffraction radiation[J].Applied Ocean Research,1995,17(2):71-77.

[10]陈智杰.波浪作用下沉管管段沉放运动的试验与数值研究[D].大连：大连理工大学，2009.CHEN Zhi-jie.Experimental and numerical investigation on the immersion motion of tunnel element under wave actions[D].Dalian:Dalian University of Technology.2009.

Effect of waves on motion characteristics of immersed tunnel element under barge rolling motion

LIU Ming1,ZHANG Jun2,ZUO Wei-guang3
（1.CCCC First Harbor Engineering Co.,Ltd.,Tianjin 300461,China;2.CCCC Fourth Harbor Consultants Co.,Ltd.,Guangzhou,Guangdong 510230,China;3.School of Water Resources,North China University of Water Resources and Electric Power,Zhengzhou,Henan 450045,China）

In the process of sinking the immersed tunnel element,the tunnel element motion is influenced by wind,wave,flow of ocean and barge.That is a very complicated hydrodynamics problem.To investigate the effect of the barge on tunnel element,assuming that the barge is forced rolling motion,it is composed of two parts for the motion of the tunnel element:one is caused by the wave and the other is caused by barge rolling motion.Time-domain model of the immersed tunnel movement is established with waves,the finite depth Green's function is used to calculate the governing equations to gain the velocity potential.Instantaneous change of the barge rolling motion is used to obtain the new displacement of the tunnel element,in which it can calculate the wave force.Wave force is applied to solve the motion equation of the tunnel element.At last the motion characteristic of the tunnel element under different amplitudes and phases are analyzed,and the relevant conclusions were given finally.

barge;immersed tunnel;rolling motion;swaying motion;low frequency motion

U459.5

A

2095-7874（2017）10-0042-05

10.7640/zggwjs201710009

2017-02-16

2017-04-03

刘明（1984— ），男，陕西富平人，博士，工程师，主要从事工程技术管理与波浪水动力学研究。E-mail：lium@ccccyhj.com