基于奇异熵增量曲率谱的信号降噪方法
胡 林, 黄文涛, 蔡 乾, 金 江
(1.华中科技大学 电子信息与通信学院,湖北 武汉430074;2.上海无线电设备研究所,上海200090)
0 引言
含噪信号的去噪问题是信号处理领域的经典问题,在工程实践中出现许多信号降噪方法,如小波与小波包降噪法[1]、减谱降噪法[2]、独立分量分析(Independent Component Analysis,ICA)降噪法[3],以及经验模态分解(Empirical Mode Decomposition,EMD)降噪法等[4]。小波降噪法的降噪效果很大程度上取决于滤波器性能的优劣,且当信号的特征频段没有先验了解或有用信号与噪声的频带交叠严重时,小波降噪法将失效。ICA降噪法要求各个源信号之间瞬时统计独立,且至多只能有一个源信号为高斯分布。EMD降噪法存在模态混淆、过包络、欠包络和瞬时频率有效性等问题。
研究表明,利用奇异值分解(Singular Value Decomposition,SVD)进行信号消噪是一种有效的降噪处理方法[5-6],降噪后的信号相移较小,且不存在时间延迟。基于SVD的信号降噪方法的关键在于有效降噪阶次的选取,现有的很多文献都是针对降噪阶次的研究,但目前还没有非常成熟和普适的方法,在工程实现中通常采用的试凑法和阈值法都依赖于使用者的经验。文献[7]提出一种利用奇异熵增量的渐近特性来确定有效降噪阶次的方法,但除了幅值的变化外,奇异熵增量曲线和奇异值曲线的形状并没有多大的区别。文献[8]提出一种根据奇异值曲率谱的最大峰值位置确定有效降噪阶次的方法,但在工程实现中曲率谱的最大峰值也有可能出现在噪声平台中。本文基于上述两种方法,提出一种基于奇异熵增量曲率谱的降噪阶次确定方法,并通过仿真试验验证了该方法的有效性。
1 奇异值分解降噪原理
假设一维信号序列x(k)混入加性高斯白噪声e(k)后得到的含噪信号序列为y(k),即有y(k)=x(k)+e(k) (1)
采用SVD降噪方法对y(k)进行降噪处理的具体实施框图,如图1所示。
实施步骤如下。
第1步,由一维含噪信号序列y(k)(k=1,2,…,N,N为数据长度)构造含噪信号矩阵Ym×n。为降低计算复杂度,当N较大时,可采用连续截断的方式将其元素嵌入到m×n维相空间内,即
第2步,对含噪矩阵Ym×n进行奇异值分解,得到主对角矩阵∑和左右正交矩阵S、D,即
其中:
式中:O 代 表 零 矩 阵;p=min(m,n);λ1≥,称为矩阵Ym×n的奇异值。
第3步,选取有效奇异值降噪阶次q,保留主对角矩阵∑m×n的前q个大奇异值,将其余的小奇异值置零,得到新的主对角矩阵∑x=diag(λ1,λ2,…,λq,0,…,0),其中q<p,且λi≠0,i=1,2,…q。
第4步,利用对角阵∑x、左右正交矩阵S和D,根据式(3)进行SVD重构运算,得到估计出的信号矩阵X^。
由奇异值分解理论可知,较大的奇异值主要反映的是信号特征,而较小的奇异值主要反映的是噪声特性,因此该方法的关键在于如何确定分解后的对角阵∑的有效降噪阶次q。当所选阶次较高时,在降噪后的信号中仍保留了一部分噪声信息,无法达到充分降噪的目的。当所选阶次较低时,降噪信号包含的信息不完整,会导致信号波形畸变,难以反映对原信号的有效信息特征。后文将重点讨论有效降噪阶次的选取问题。
2 奇异熵增量曲率谱
在有效降噪阶次的选取方面,目前使用较广泛的是文献[7]提出的一种方法,它将奇异熵增量开始降低到渐近值时所对应的阶次作为降噪阶次。奇异熵增量定义为
并非所有含噪信号的奇异熵增量曲线都存在明显的渐近值,且从本质上说,除了幅值的变化外,奇异熵增量曲线和奇异值曲线的形状并没有多大的区别,即没有明显的特征可以用来确定有效降噪阶次。
文献[8]提出一种根据奇异值曲率谱的最大峰值位置确定有效降噪阶次的方法,但射频前端实采数据的奇异值较大,噪声平台对应的小奇异值远大于0,且其值大幅度下降,导致其曲率谱的最大峰值有可能出现在噪声平台中。
奇异熵增量从幅值上可以理解为归一化后的奇异值,其噪声平台对应的奇异熵增量均接近0。由此,本文提出一种根据奇异熵增量曲率谱来确定有效降噪阶次的方法。连续曲线l(t)上各点曲率的计算公式为
奇异熵增量曲线ΔEi由一系列离散点构成,计算各点的曲率时用对应的差分公式来代替上式中的导数,即
曲率谱反映的是各奇异熵增量的转折程度,曲率越大,奇异熵增量的转折程度越大,则奇异值在该处的变化越大。由理想噪声构造的矩阵的所有奇异值大小相等,实际噪声构造的矩阵中后面的奇异值会有一定幅度的下降,但这种下降是连续平滑的,且幅度很小,所以其奇异熵增量曲线没有转折点,曲率接近零。由此可以认为,当奇异熵增量的曲率降到趋于零时(设一个很小的正数作为判决阈值,即当奇异熵增量曲率降到小于阈值时,则认为达到了零值),信号的有效特征信息已趋于饱和,此时对应的位置即为有效降噪阶次q。
图2为射频接收前端实采短波信号的仿真,其中,图2(a)为该信号的奇异值曲线,图2(b)为该信号的奇异值曲率谱,图2(c)为该信号的奇异熵增量曲线,图2(d)为该信号的奇异熵增量曲率谱。对比图2(a)和图2(c)可见,除了幅值不同以外,这两条曲线在形状上的确没有明显的特征差异,即采用基于奇异熵增量的方法难以选取有效降噪阶次。由图2(b)可见,该曲线的最大峰值的确出现在噪声平台中(q=133),因此也不能依据奇异值曲率谱的最大峰值来选取有效降噪阶次。由图2(d)可见,该实采短波信号的有效降噪阶次以确定(q=33),即采用本文提出的基于奇异熵增量曲率谱的方法能够较准确地选取到有效降噪阶次。
3 仿真实验
3.1 仿真信号的验证实验
(1)双窄带通信号
为验证所提出的降噪方法的有效性,对通带分别为7 MHz~8 MHz和15.5 MHz~16.5 MHz的双窄带通信号以不同的信噪比加入高斯白噪声,对其进行降噪处理,比较降噪前后的信噪比。实验时采用的数据长度为65 536个点,构造的矩阵规模为256×256。分别以5 dB、10 dB和15 dB的信噪比加入高斯白噪声后进行降噪处理,得到的仿真结果如图3所示。其中,图3(a)和图3(b)分别为信噪比为5 d B时降噪处理前后的功率谱图,图3(c)和图3(d)分别为信噪比为10 dB时降噪处理前后的功率谱图,图3(e)和图3(f)分别为信噪比为15 dB时降噪处理前后的功率谱图。表1则给出了仿真结果的具体数值。
可见,从功率谱上看,所提出的降噪方法具有较为明显的降噪效果,可将本底噪声降低10 dB左右。从降噪处理前后的信噪比来看,原含噪信号的信噪比越低,改善量越可观,而当原信号本身的信噪比已经足够高时,改善量则有限。
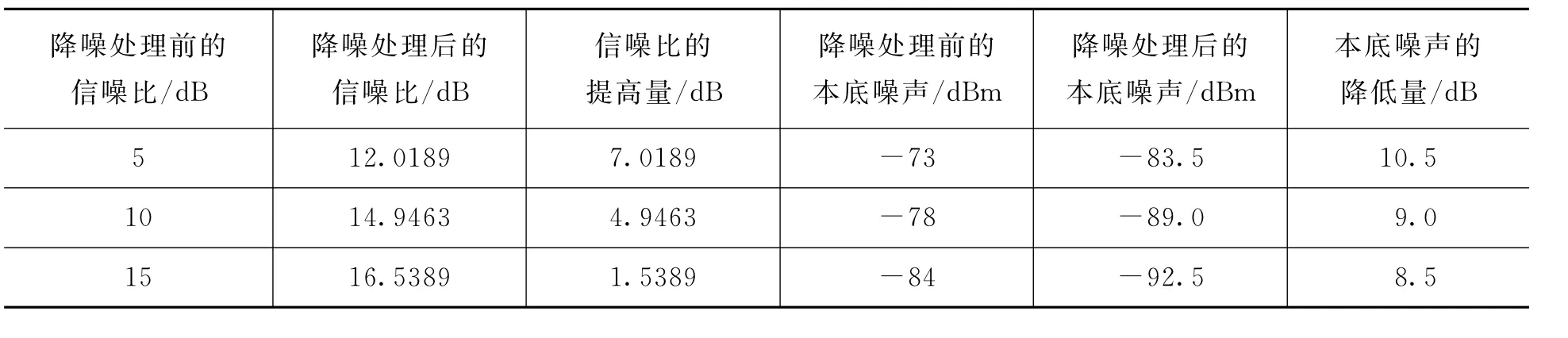
表1 双窄带通信号仿真结果
(2)等幅三频加16QAM小信号
再以一个等幅三频加16QAM小信号为例,进一步说明所提出的降噪算法的有效性。其中,等幅三频信号的频率位置分别为6.1 MHz、7.6 MHz和10.9 MHz;16QAM小信号的中心频率为9.43 MHz,波特率为500 kbps,成型滤波器滚降系数a=0.5。实验时采用的数据长度为65 536个点,构造的矩阵规模为256×256。对其进行降噪处理,仿真结果如图4所示。其中,图4(a)为原含噪信号的功率谱图,图4(b)为经过降噪处理后的输出信号的功率谱图。
可见,原含噪信号的本底噪声为-103 dBm,降噪处理后的本底噪声为-111 dBm,即可将本底噪声降低8 dB。此外,对降噪处理后的16 QAM小信号进行解调,可以得到较好的解调效果,即该降噪处理过程能够保证信号所含信息的完整性。
3.2 实采信号的验证实验
为更好的验证本文提出的SVD降噪算法的降噪性能,图5给出了对短波数字接收前端实采的不同类型信号进行降噪处理前后功率谱对比图。其中,图5(a)为实采的双16 QAM信号,中心频率分别为9 MHz和12 MHz,波特率为1.25 Mbps,成型滤波器滚降系数为0.5。图5(b)为该双16 QAM信号的降噪输出。图5(c)为实采的等幅三频信号与小功率16 QAM信号的组合信号,三频信号的中心频率分别为7 MHz、16 MHz和22 MHz,16 QAM信号的中心频率为9 MHz,波特率为0.25 Mbps。图5(d)为该组合信号的降噪输出。图5(e)为实采的大功率16 QAM信号与小功率16 QAM信号的组合信号,大功率16 QAM信号的中心频率为9 MHz,波特率为1.25 Mbps,小功率16 QAM信号的中心频率为18 MHz,波特率为0.25 Mbps。图5(f)为该组合信号的降噪输出。
由图5可见,所采用的数字接收前端的输出信号的本底噪声水平已经比较低,但采用本文提出的SVD降噪算法仍能改善4 d B~8 d B左右,且对各种类型的信号均有效。
尤其值得注意的是,图5(d)和图5(f)中降噪处理后的小功率16 QAM信号均可解调,即该降噪处理过程在降噪的同时能够保证信号所含信息的完整性。
4 结论
本文将奇异值分解降噪法用来降低数字接收前端的本底噪声,提出的根据奇异熵增量曲率谱特性来确定降噪阶次的方法取得了较好的降噪效果,且能够保证信号的完整性。将该方法应用于数字接收前端时,可改善其噪声系数和接收灵敏度,并提高微弱信号的发现和检测概率,有效增大接收前端动态范围。

