基于零阶算法的矩形面宽带纵振换能器设计

马雄超，赵荣荣，唐少波，于祥龙，欧阳荀



基于零阶算法的矩形面宽带纵振换能器设计

马雄超1，赵荣荣2，唐少波1，于祥龙1，欧阳荀1

(1.上海船舶电子设备研究所，上海 201108； 2.水声对抗技术重点实验室，上海 201108)

传统换能器的优化一般采用试算修改的方式进行，这样的方式在待优化参数较多时不仅比较繁琐而且有可能会漏掉各参数组合下较好的设计点，对此提出了利用零阶算法进行换能器多参数联合优化设计的方法。建立了一种带宽评价函数，通过该评价函数和零阶算法尝试了对矩形面纵振换能器带宽的优化设计。经有限元仿真和样机测试表明，两款换能器的性能达到了预期指标要求，实现了宽带工作。得到的两款宽带换能器性能为：1#换能器工作频带为10~21.5kHz，带内起伏约3dB，发射电压响应大于134dB；2#换能器工作频带为7.5~31.5kHz，带内起伏约6dB，发射电压响应大于131dB。该方法可以作为换能器设计的一种新方式。

零阶算法；评价函数；宽带；矩形面纵振换能器

0 引言

纵振换能器是水声领域比较常见的换能器类型之一，因其具有结构工艺简单、性能稳定、等效机电耦合系数高、功率重量比大等优点而得到了广泛的应用，但是传统纵振换能器的工作带宽都比较窄，常不能满足一些声呐的指标要求[1-2]。

为得到宽带特性,设计人员采用了多种方法，如匹配层技术、多模态耦合技术、新材料技术等[3],这使换能器的结构变得越来越复杂，若要使换能器工作在指标要求的频带，设计人员往往都需经过很长时间的仿真试算和试验摸索。张文波以及A.V.Nasedkin等人运用了不同的优化算法[4-5]对匹配层的杨氏模量、长度、孔隙率等参数分别进行了单参数的独立优化设计，较传统的设计方式更加严谨、快捷，但仍然有可能漏掉各个参数组合最优的情况，且结果并不一定准确可靠。

目前换能器的优化设计大都还是依照试算修改的方式进行，设计周期一般比较长。当要设计宽带换能器而有限元模型较大时，直接将计算的声压值或者响应值作为目标函数来优化工作带宽，却又是极其耗费计算机内存和机时的。在光学设计中针对不同像差有各类相应的评价函数，设计人员一般通过ZEMAX软件求评价函数的最小值即可实现满足指标要求的理论设计，在此启发之下，本文先自行建立了一种带宽评价函数，然后代入ANSYS优化模块作为目标函数，再采用其零阶优化算法进行多参数联合优化，以此来尝试解决有限元模型为三维的矩形面纵振换能器宽带工作的问题。

1 模态耦合与换能器结构

从物理的角度，换能器是一个无限维的连续振动系统，存在无限个各自分立的本征频率，它的应变能主要都以这些分立的模态来释放。而实际中只能激励出有限个模态，最早先的纵振动换能器主要以相互对称的奇数阶纵向模态工作，这些模态的频率间隔较大，难以实现耦合。后来发现只要合理设计结构，还可以激励出如弯曲振动等其他模态，再进行优化改进，即可通过模态耦合，实现频带展宽。在纵振换能器的结构设计中，为了增加弯曲振动的模态参与因子以及让声波能量充分向水中辐射，常将辐射头设计成喇叭型。本文待优化的换能器正是这种结构，它主要由前盖板(铝)、压电陶瓷(PZT4)、预应力螺杆(45#钢)、后盖板(45#钢)组成，具体形式如图1所示。

图1 换能器的结构

2 换能器结构优化

从数学的角度,任何设计问题都可以看成是在可行域内求极值的问题,换能器的设计也不例外。在带宽设计中，换能器的模态虽然不能随心所欲地激励出来，也难以随心所欲地实现耦合，但是利用优化算法可以去选择预期的工作频带所对应的始末模态频率，以及其间有可能实现较好耦合的模态频率，从而实现宽带设计的目标。利用优化算法设计换能器带宽，实质是一个选模的过程。该方法可以在不使用其它宽带技术时，充分发掘结构自身的模态耦合潜能。

2.1 零阶算法

零阶算法是一种曲线拟合求最优值的方法。大部分文献的研究[6-8]指出，该方法相比其它方法具有较高的优化效率和可观的精度且不易陷入局部极值点的优点。ANSYS零阶算法已被广泛地应用于各种机械结构的优化设计中。它先通过添加惩罚函数将受约束问题无约束化，然后在初始设计点附近随机选取采样点拟合出目标函数与设计变量之间的关系，再根据拟合出的函数关系求解目标函数的极值点，从而求出对应的设计点。以此设计点再开始循环迭代，直至求出满足收敛条件的最优设计点。相比其它优化方法，零阶算法属于一种粗优化方法，但对于一些复杂的计算模型、较大的机械结构，采用该方法仍然是比较适宜的。文献[7]的研究指出，一阶算法的耗时一般在零阶算法的5到10倍左右，两者计算结果相差基本在0.05%以内。ANSYS优化模块集成了这种算法，这使得在ANSYS里进行优化设计更加便捷。

2.2优化模型的建立

一个优化数学模型的建立除了需要优化迭代算法化外，还需要设计人员自行设定设计变量、状态变量以及目标函数。这些变量及函数对应换能器待优化设计的各个结构参数和各个性能指标。对设计变量的取值范围进行约束，可以控制换能器的结构尺寸大小，对状态变量和目标函数的约束可获取预期的性能。但是在设定它们之前必须有一个参数化的有限元模型。ANSYS的APDL语言恰好为此提供了条件。本文建立的有限元模型如图2所示，其中，由于换能器辐射头是主要优化的结构，其形状会发生各种调整和变化，为了避免网格划分失败而引起优化迭代停止，采用了较细的六面体网格。有限元模型单元个数约为34万，求解方程个数约为38万。

图2 1/4有限元模型

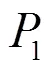
ANSYS结构优化时，设计变量一般为正，所以通过长度差和宽度差的设定可保证计算出的辐射头仍为喇叭型。为了保证这种结构故未将等参数直接作为设计变量。

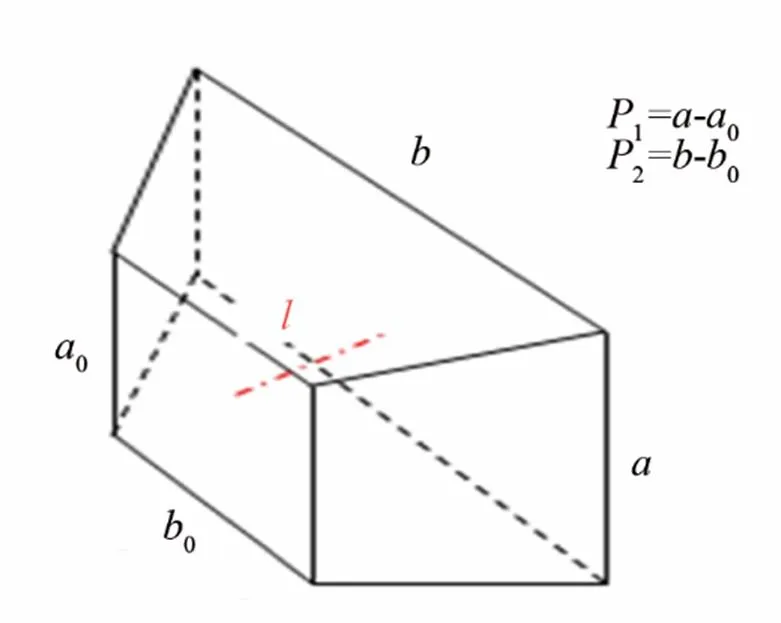
图3 辐射头优化参数示意图

图4声压频响曲线

设为从0~等间隔取的频率点个数，理论上0到间取得等间隔频率点个数越多，带内起伏Δ越小，即：

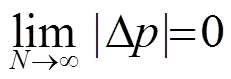
考虑到实际优化的计算效率，本文共取了3个频点，所以带宽评价函数相应地建立如下：

(3)

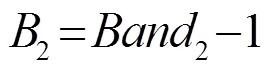
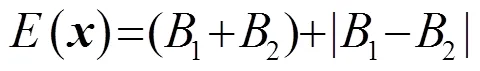
2.3优化结果

使用双核CPU，主频3.3GHz，线程数24，可用RAM大小36G的工作站进行零阶优化，迭代次数设置为30，经大约6*2h后分别计算出了两款换能器的31个设计点，()最终分别收敛到0.16531，0.048820。具体寻优过程如图5和图6所示。

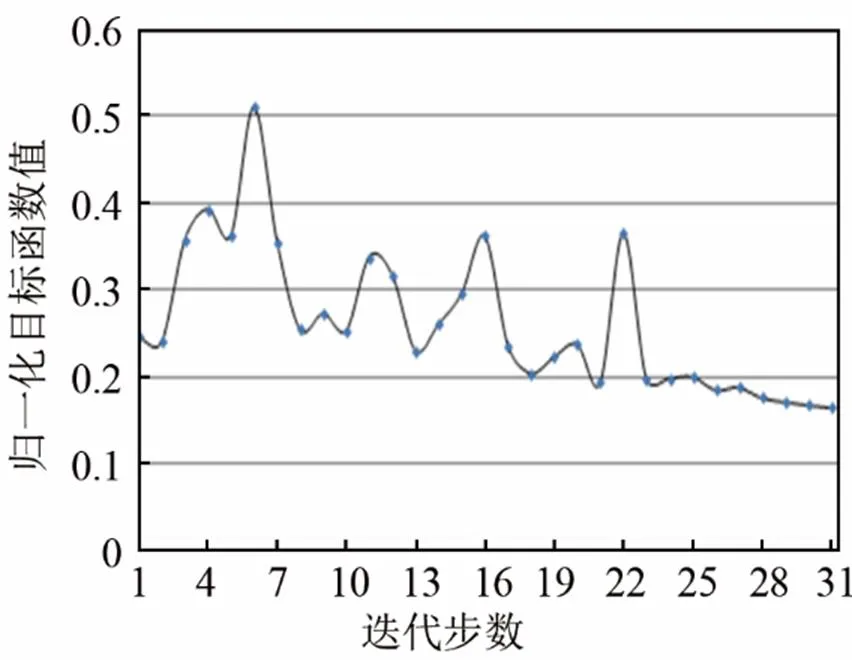
图5 1#换能器的优化迭代过程

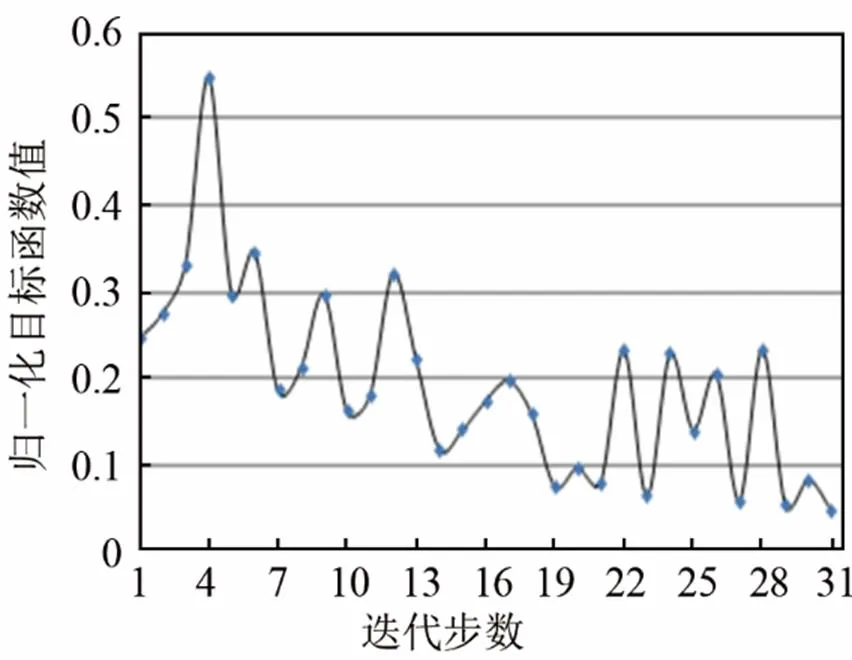
图6 2#换能器的优化迭代过程

Fig.6The optimization iterative process for2#transducer

表1优化迭代算出的尺寸参数大小(单位：mm)

Table 1 The calculated sizes of the transducers by optimal iteration

2.4ANSYS仿真验证

大量的换能器设计实践表明ANSYS可作为换能器性能预报的可靠工具。ANSYS采用了fluid130单元结合吸收属性模拟了无穷远三维水体的吸收边界条件，可以计算出换能器在自由场条件下的发射电压响应曲线。为初步验证优化结果，将优化迭代得到的结构参数值代入ANSYS进行有限元仿真，仿真结果如图7和图8所示。

由图7可知，1#换能器的理论工作频带为10~24.5 kHz，带内起伏约3dB，发射电压响应大于135dB；由图8可知2#换能器的理论工作频带为7.5~33 kHz，带内起伏约5dB，发射电压响应大于134 dB。其中2#换能器出现了3个谐振峰，通常纵振换能器只有纵弯两个模态。对此，可用ANSYS进行结构模态分析，通过处理后可画出速度或者位移的矢量图如图9~10所示。

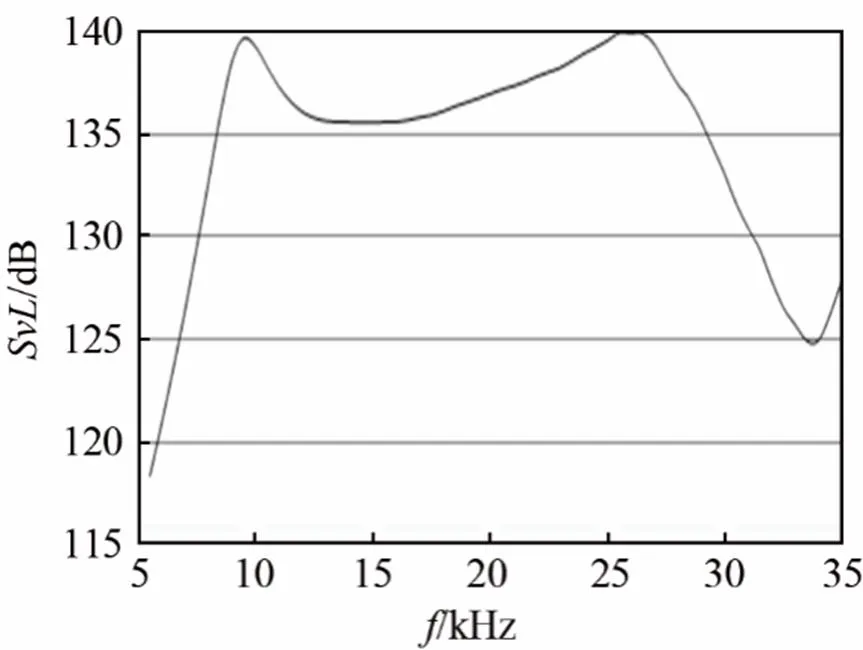
图7仿真的1#换能器的水中发射电压响应

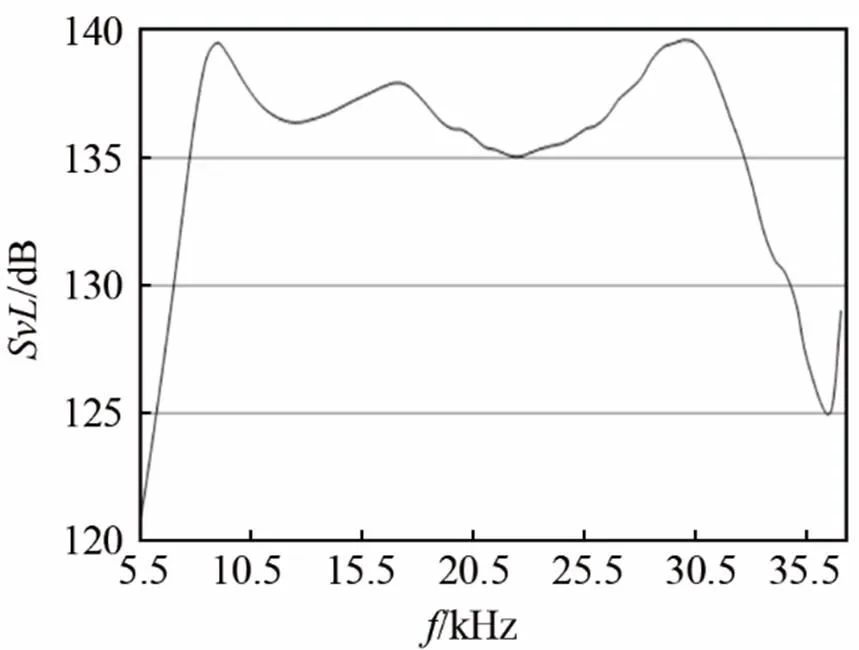
图8仿真的2#换能器的水中发射电压响应

一阶模态二阶模态

一阶模态二阶模态三阶模态

从图9、10可看出，前两阶模态对应着传统纵弯耦合换能器的纵振和弯振，而2#换能器的第三阶模态是辐射边上的一个高阶模态，由于辐射面较大，该边上已经出现了反相节点。

3 样机制作与测试

根据优化计算出来的结构参数值，实际制作了样机。本文选取了硬铝作为换能器外壳材料并采用聚氨酯灌封工艺进行了水密，实物如图11所示。

图11换能器实物图

换能器制作完成以后，在消声水池进行了性能测试，测试项目为水中电导()和水中发射电压响应()，测试结果见图12～15。

图12 实测的1#换能器的水中电导曲线

实测1#换能器的工作频带为10~21.5 kHz，带内起伏约3dB，发射电压响应大于134 dB。2#换能器的工作频带为7.5~31.5 kHz，带内起伏约6dB，发射电压响应大于131 dB。

将图7与图13、8与图15进行对比发现，仿真曲线和实测曲线整体趋势基本一致，但在一些频点也存在差异，分析原因在于：(1) 本文仿真时换能器的外壳假定为①绝对刚性的、②与换能器振子绝对去耦，而实际铝制外壳为弹性，且去耦材料并不能完全去耦；(2) 三维有限元模型由于计算量较大难以将网格取得较细从而使计算有一定的误差；(3)仿真时未将计入灌封橡胶的影响，结合实验和模态分析结果可推测，1#换能器的第二阶模态(弯曲振动)相比其第一阶模态(纵振)有可能是更易受到灌封橡胶的影响，而2#换能器的高阶弯曲振动应该受此影响较小，故导致了1#换能器的带宽内后一个谐振点前移比2#换能器带内最后一个谐振点前移明显。

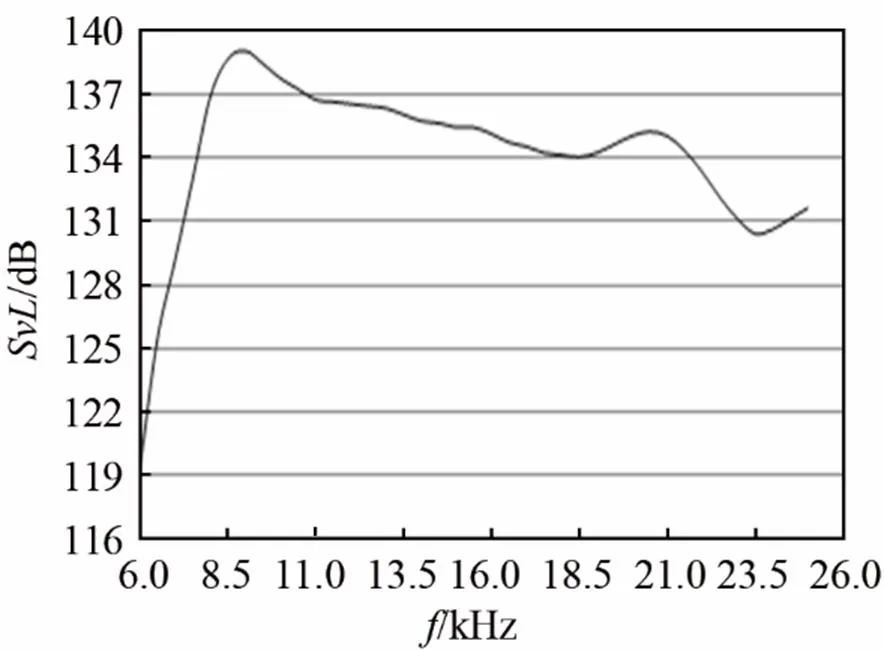
图13实测的1#换能器的水中发射电压响应

图14实测的2#换能器水中电导曲线

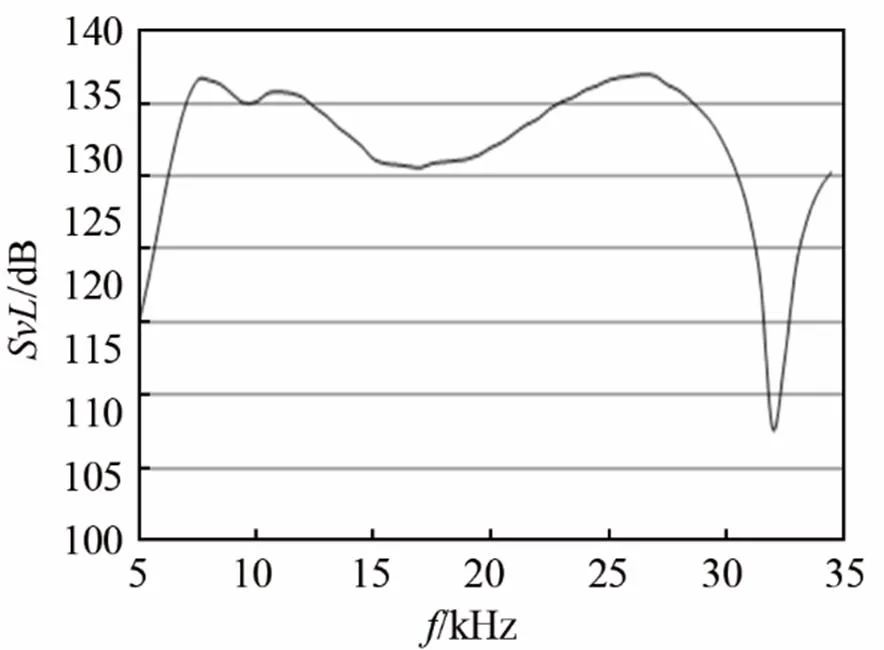
图15实测的2#换能器的水中发射电压响应

4 结论

本文提出了利用零阶算法进行换能器多参数联合优化设计的方法，建立了一种带宽评价函数，通过该评价函数和零阶算法对矩形面纵振换能器的带宽进行了优化设计，有限元仿真和样机测试结果表明：

(1)使用该带宽评价函数优化设计的换能器其性能基本达到了预期指标要求；

(2)该评价函数结合零阶算法可用于有限元模型较大的换能器宽带设计；

(3)该方法可以作为换能器设计的一种新方式。

[1] 唐少波, 赵荣荣, 田辉, 等. 一种带障板宽波束宽带纵振动换能器[J]. 声学技术, 2014,33(2):184-188. TANG Shaobo, ZHAo Rongrong,TIAN Hui,et al.Akind of wide-beam broad-band longitudinal vibration transducer with a plate[J]. Technical Acoustic, 2014,33(2): 184-188.

[2] 于祥龙, 赵荣荣, 唐少波. 一种矩形辐射面宽波束换能器的设计[J]. 声学技术, 2015, 24(1):58-60, 63. YU Xianglong, ZHAO Rongrong, TANG Shaobo. Design of a wide-beam rectangular radiation transducer[J]. Technical Acoustics, 2015, 24(1): 58-60, 63.

[3] 刘慧生, 莫喜平. 纵向换能器宽带研究设计进展[J]. 声学技术, 2014, 33(6):564-571. LIU Huisheng, MO Xiping. Progress in research and design of broadband longitudinal transducers[J]. Technical Acoustics, 2014, 33(6): 564-571.

[4] 张文波, 王明洲, 赫保安. 宽带水声换能器电声性能的优化设计[C]//2011年优秀论文集,中国造船工程学会,2012. ZHANG Wenbo, WANG Mingzhou, HE Baoan.Optimization design of broadband underwater acoustic transducer [C]//2011ChineseShipbuilding Engineering Society symposium, China Shipbuilding Engineering Society,2012

[5] Nasedkin AV,Shevtsova MS,LIUJC, et al.Multiobjective optimal design of underwater acoustic projector with porous piezocomposite active elements[J].Journal of Applied Mathematics and Physics,2013,1(6): 89-94.

[6] 项青, 尹征南, 秦昊. 基于零阶算法的轨道吊结构优化设计[J]. 上海大学学报, 2015, 21(6): 742-748. XIANG Qing, YIN Zhengnan, QIN Hao. Optimal design of track hanging structure using a zero-order algorithm [J]. Journal of Shanghai University, 2015, 21(6): 742-748

[7] 郭彤, 李爱群, 费国庆. 零阶与一阶优化算法在悬索桥模型修正中的应用对比分析[J]. 振动与冲击, 2007, 26(4): 35-38. GUO Tong, LI Aiqun, FEI Guoqing. Comparative analysis of the application of zero order and first order optimization algorithm in the correction of the model of suspension bridge[J]. Journal of Vibration and Shock, 2007, 26(4): 35-38.

[8] 严云.基于ANSYS 参数化语言的结构优化设计[J]. 华东交通大学学报, 2004, 21(4):52-55. YAN Yun. Design of Structure optimization with APDL [J].Journal of East China Jiaotong University, 2004, 21(4): 52-55.

A design of rectangular longitudinal vibration broadband transducer based on zero order algorithm

MA Xiong-chao1, ZHAORong-rong2, TANGShao-bo1, YU Xiang-long1, OUYANG Xun1

(1. Shanghai Marine Electronic Equipment Research Institute, Shanghai201108, China;2. Science and technology on Underwater Acoustic Antagonizing Laboratory,Shanghai201108, China)

The optimization of the traditional transducer generally adopts the way of trial calculation, which is not only tedious but also may miss the better design points under the combination of various parameters.For those reasons, a joint multi parameter optimization method based on zero order algorithm is proposed, and a bandwidth evaluation function is established. With the help of the evaluation function and the zero order algorithm,the bandwidth optimization of rectangular plane longitudinal vibration transducer is achieved. Simulation and experimental results show thatthe performances of the two transducers meet the requirementof broadband,the evaluation function is feasible and can be used in the optimization of the transducer.The performances of the two transducers are as follows: for 1#transducer the frequency band is 10~21.5 kHz, the band flatness is about 3 dB and the transmitting voltage response is greater than 134 dB; for 2#transducer the frequency band is 7.5~31.5 kHz,the band flatness is about 6 dB and the transmitting voltage response is greater than 131 dB.This method can be used as a new way to design transducer.

zero order algorithm; evaluation function; broadband; rectangular plane longitudinal vibration transducer

TB556

A

1000-3630(2017)-01-0093-06

10.16300/j.cnki.1000-3630.2017.01.017

2016-11-10;

2016-12-28

马雄超(1990－), 男, 重庆人, 硕士研究生, 研究方向为水声换能器与基阵。

马雄超, E-mail: 2448908303@qq.com