石英摆片灵敏度的测试方法研究

王佳佳 邵竹锋 隋 梅 王玉芬（中国建筑材料科学研究总院，北京 100024）

石英摆片灵敏度的测试方法研究

王佳佳 邵竹锋 隋 梅 王玉芬（中国建筑材料科学研究总院，北京 100024）

作为惯性测量与导航系统的核心元件，石英摆片在国防和民用领域皆有重要应用。但是石英摆片存在灵敏度无法准确测量的缺点，严重制约着我国惯性导航技术的发展。本文从石英摆片的结构模拟着手，利用下摆量的指标来考核石英摆片的灵敏度。

石英摆片；挠性加速度计；灵敏度

1 引 言

石英玻璃挠性加速度计作为惯性导航和遥控遥测仪表在航天、航空、航海技术领域占有重要地位，石英玻璃挠性加速度计还广泛应用于石油钻井、开凿隧道、地震测量、精密器械运动测量等民用领域[1]。石英玻璃摆片是挠性加速度计的核心敏感元件。石英摆片的内在质量和加工精度直接影响加速度计的使用性能，从而影响到惯性导航的精确度与可靠性。

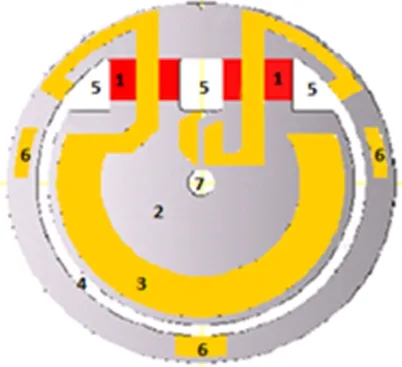
图1 石英摆片示意图

石英摆片整体结构是由直径25mm，厚度约0.8mm的石英玻璃片构成[2]，分为外环和内摆两部分，外环和内摆由大约30µm厚的挠性支撑梁连接（如图1所示）[3,4]。微小力的冲击就会引起内摆的震动。挠性梁作为整个内摆的支撑部件，须有足够的灵敏度[5,6]。目前，对于摆片的挠性支撑梁的灵敏度尚没有建立起有效的检测手段。经过测试发现石英摆片的灵敏度和挠性梁厚度有着对应关系，但是挠性梁的厚度需要通过破坏的方法才能测量，本文通过测量内摆的下摆量来表征挠性梁的厚度，进而表征挠性梁的灵敏性。

2 模型的建立

文章认为石英摆片挠性梁的性能与材料力学中的变形固体的性能相似，因此可以借用变形固体的模型。石英摆片水平放置时，内摆受重力而下摆，该重力使挠性梁的右端产生大小为M0的弯矩(如图2所示)。因此，可将石英摆片挠性梁看成是厚h(µm)，宽度b=8.2mm，一端固定，一端形成弯矩M0的悬臂梁。

图2 摆片水平放置时的受力示意图

3 摆片下摆量和挠性梁厚度的理论计算

3.1 内摆重心的确定

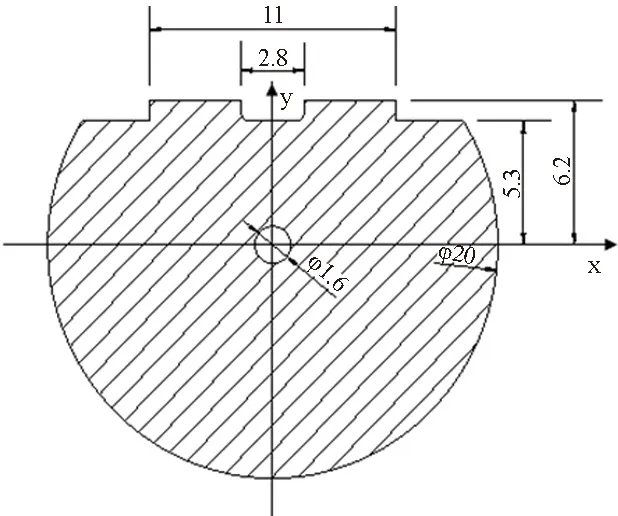
图3 内摆的坐标图

借助弹性力学原理计算挠性梁的厚度h和内摆下摆量Ymax之间的关系，首先要求解决内摆的质量和重心的位置。为便于计算，以内摆中心孔为中心建立坐标轴，并将内摆的各参数标于图3上。

计算步骤如下：

1）内摆质量的求算

内摆为厚度是0.722mm的薄片，质量计算式为：

2）重心位置的确定

图4 内摆的区域划分示意图

为了确定内摆重心的位置，将内摆假设成厚度为0.722mm的圆形薄片去除中心孔O，和D区域后的阴影区域（见图4所示），再将阴影区域划分为A、B、C三个区域。

由物理学知识知道，内摆的重心坐标公式为：

由于内摆是一个关于Y轴对称的图形，因此重心横坐标x0=0。

假定内摆的厚度均匀，密度均匀。则式（2）中的mi为：

将式(2)中的ρ从分子、分母中约去，这样式(2)成为：

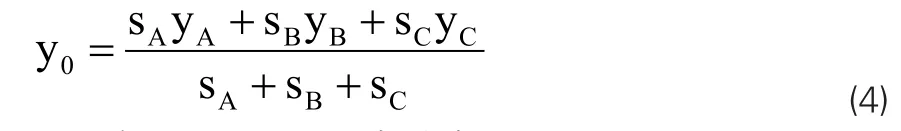
图4中，图形B、C为对称图形，所以，

sB=sC=3.69mm2，yB=yC=5.75mm。

A区则为同心圆环O除去弦EF以上的半圆区D，其面积SA可由下式得出：

sA=257.77-2=255.77mm2

A区的重心纵坐标yA可有下式得出：

显然同心圆O关于x轴对称。所以yO=0，代入(5)式得：

D区的重心坐标yD可由以下定积分得出：

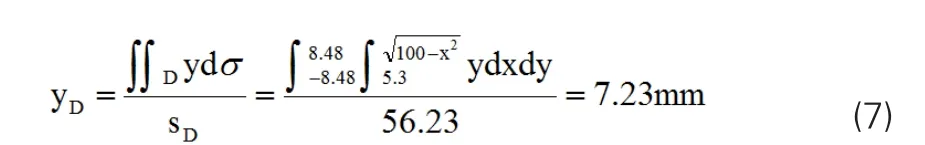
将yD、sA、sD代入(6)式得：

将sA、sB、sC、yA、yB、yC代入式(4)中得：

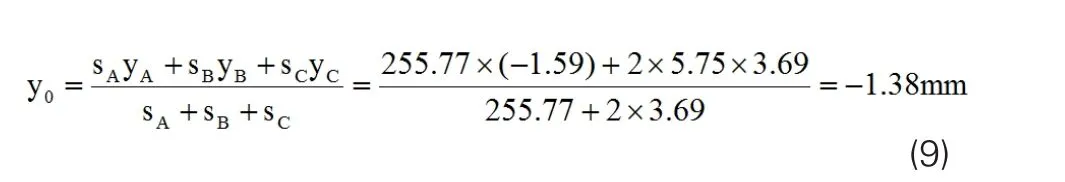
因此，内摆的重心在图4所示的原点下方1.38mm处。

3.2 内摆下摆量和挠性梁厚度的理论关系

计算内摆下摆量和挠性梁厚度的理论关系式，可分以下几步：

1）弯矩的计算

内摆重心到梁的距离：

d=1.38+6.20=7.58mm

由此，内摆的重力对梁产生的弯矩M0为：

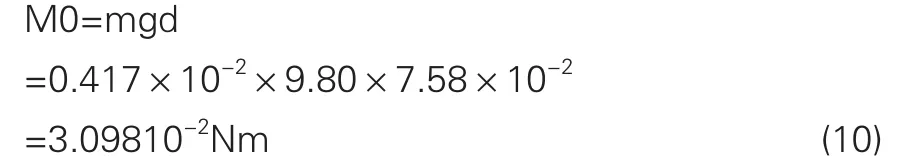
2）挠性梁惯性矩的计算

图5 挠性梁的侧面示意图

可将挠性梁看成高h，宽度b=8.2mm的悬臂梁，其侧面图示于图5。取微截面dA=bdy,则有惯性矩的定义，积分得：

3）最大偏角的计算

由此，根据弹性力学得出，挠性梁最大偏角方程为：

l是长度，EI是弯曲刚度。

4）最大下摆量的计算

当摆片水平放置时，内摆自然下垂，从内摆的最端部向水平方向做垂线，可以得到一直角三角形，其中角θmax就是该直角三角形的一个锐角，内摆的长度即该直角三角形的斜边。由此，角θmax的对边即内摆的下摆量Ymax，可用下式求得：

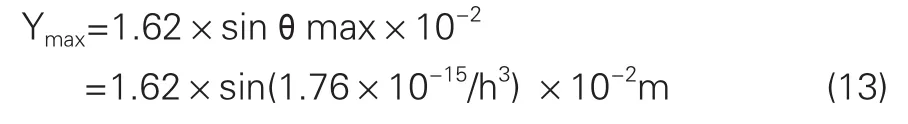
因此，式(13)即为内摆的下摆量和挠性梁厚度的理论关系式。

4 内摆下摆量的试验测试

将石英摆片的外环放置在带孔的平台上，内摆在孔内自然下垂，测量平台和内摆最低点的距离就可测得摆片的实际下摆量。

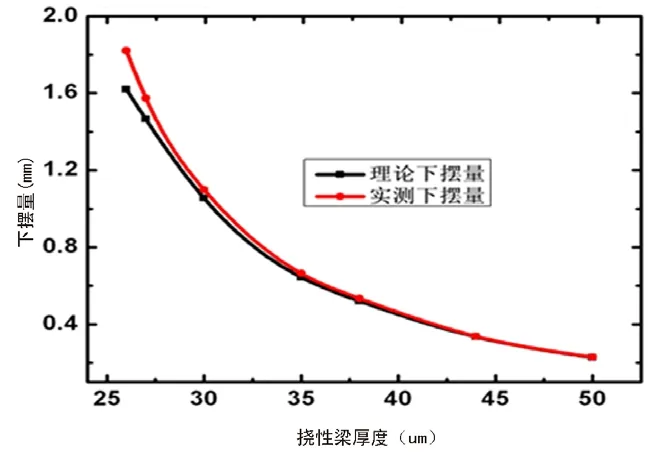
图6 石英摆片下摆量和挠性梁厚度的关系

将摆片破碎，取出挠性梁，用螺旋测微器测得挠性梁的实际厚度。Ⅳ类石英摆片的理论下摆量和实测下摆量随厚度的变化关系绘于图6。由图中可见，在挠性梁较厚时，理论值和实测值非常吻合；但是，随着挠性梁的减薄，实测下摆量的数值超过理论下摆量。其原因是：1）公式13是以弹性力学变形固体的模型为依托的，当挠性梁的变形较大后，挠性梁的实际性能偏离了变形固体的理论假设；2）当挠性梁达到很薄的尺寸时，表面和内部的缺陷使得弹性模量的数值降低。

5 结 语

摆片灵敏度由挠性梁的厚度决定，因此可用挠性梁的厚度表征灵敏性。由于摆片形状的限制，挠性梁的厚度尚无法直接测量。本文通过测量内摆的下摆量来表征挠性梁的厚度，进而表征挠性梁的灵敏性。文章建立了挠性梁下摆量和厚度的关系公式，并通过破坏法测出了挠性梁的实际厚度，发现计算值和实际值吻合。

[1]吕志清,侯正君.线性加速度计的现状和发展动向.压电与声光,Vol.20,No.5,1998,6:313-321

[2]袁峰.石英摆片加工工艺的研究.哈尔滨工业大学硕士学位论文,1988

[3]施平,袁峰,梁志兴等.石英摆片加工过程中若干问题的研究.哈尔滨工业大学学报,1993,25（6）:86-89

[4]周岩等.石英摆片成形工艺研究.航天工艺,N0.5,1999,10:23-27

[5]林庄,袁峰,黄鸿斌等.摆片工艺流程的研究.哈尔滨工业大学学报,1993,25（2）:18-24

[6]周岩,刘晓胜,杨乐民等.石英器件加工工艺最新进展.中国机械工程，Vol.11,No.6,2000,6:668-670

The study of sensibility testing to quartz pendulous reed

As a key part in the inertial measure and guidance system,quartz pendulous reed is of great importance in national defence and civil field.But the flexible beam of quartz pendulous reed has poor rate of no method to test its sensibility,that restricts the development of our country’s inertial guidance technology.This article worked from numerical simulation of quartz pendulous reed to check the sensibility by drop size.

quartz pendulum;flexible accelerometer;sensitivity

TQ171.7

B

1003-8965（2017）04-0043-03