中考几何最值问题解法研究

应中伟

摘 要：几何最值问题是中考的热点，也是初中数学教与学的一类重点和难点。几何最值问题的逻辑性思维较强，并不像方程等代数问题解法上比较单一。本文对近几年浙江台州中考试卷中的最值问题做了分析，并对此提出中考几何最值问题的解题方法。

关键词：公理法；数形结合；旋转转化；构造特殊位置

一、几何公理法

在几何最值上出现频率最高的问题就是周长、面积、角度以及线段的最值问题，几何公理法对于解决此类问题无疑是一个容易运用的方法。几何最值的基本公理有两点之间线段最短，垂线段最短和利用函数关系求最值。

例1 （2012·浙江台州）如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（）

分析：遇到这种最值问题最好的解决方法就是将题目中隐含的条件找出来，运用几何的基本公理去将题目化简，最后得出我们想要的答案。具体如右图所示，先利用对称的特性找出点K1的位置就是我们所要求的点K的位置。然后由三角形两边之和大于第三边的性质，得出P1K+QK>P1Q=P1K1+QK1=PK1+QK1，再根据菱形的性质，计算得到答案选B。这样的题目对于学生而言最关键的就是找到突破口和对公式定理的熟练运用。几何的定理并不是独立存在的，多个公理都可以应用在同一道题目，甚至同一种题型中。

归纳：几何公理法是解决几何最值问题中最常见，也是最简单有效的一种解法。这类线段或角度的几何最值问题我们可借助图形的平移、旋转和翻折将问题转化为两点之间线段最短，垂线段最短这样的几何原理来解决。

例2 （2017·浙江台州）交通工程学理论把在单向道路上行驶的汽车看成连续的液体，并用流量、速度、密度三个概念描述车流的基本特征。其中流量q（辆/小时）指单位时间内通过道路指定断面的车辆数；速度v（千米/小时）指通过道路指定断面的车辆速度；密度K（辆/千米）指通过道路指定断面单位长度内的车辆数。为配合大数据治堵行动，测得某路段流量q与速度v之间的部分数据如下表：

（1）根据上表信息，下列三个函数关系式中，刻画q，v关系最准确的是________（只需填上正确答案的序号）

（2）请利用（1）中选取的函数关系式分析，當该路段的车流速为多少时，流量达到最大？最大流量是多少？

分析：（1）③（2）解：∵q=-2v2+120v=-2（v-30）2+1800.∴当v=30时，q最大=1800。

归纳：利用函数关系求最值是几何最值问题中比较经典的一类问题，它具有清晰的解题方向与步骤，具体的解题方法是先根据实际问题选择或建立适当的函数模型，然后借用函数关系式在自变量的取值范围内求出最值。

二、数形结合法

数形结合法旨在通过对数学研究中的数、形这两个基本对象进行转化，从而解决一系列的数学问题，它是数学学习中很常用的一种思想。具体可分为两种情况：①通过数字的准确性来描述形状的一些属性。②通过几何直觉的形状来验证一些数之间的关系。在几何最值问题上我们也经常使用数形结合的数学思想来解决问题。

例3 （2012·浙江台州）定义：P、Q分别是两条线段a和b上任意一点，线段PQ长度的最小值叫作线段与线段的距离。已知O（0，0），A（4，0），B（m，n），C（m+4，n）是平面直角系中四点。

（1）根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离是_____，当m=5，n=2时，如图2，线段BC与线段OA的距离（即线段AB的长）为______

（2）如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式。

（3）当m的值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M。

①求出点M随线段BC运动所围成的封闭图形的周长；

②点D的坐标为（0，2），m≥0，n≥0，作MH⊥x轴，垂足为H，是否存在m的值，使以A、M、H为顶点的三角形与△AOD相似，若存在，求出m的值；若不存在，请说明理由。

归纳：在这种问题的解决上如果仅仅从几何的定理出发，很难解决，从本题的知识考察点来看是典型的数形结合问题。遇到这样的题目只能从数与形之间的关系出发，寻找到解题的关键。

三、旋转转化法

旋转是解决几何问题的最常用手段。旋转可以将几何图中的各种图形相关联，以找到我们需要的关系，然后使用现有知识来解决问题。

例4 （2013·浙江台州）如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2，中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（）

归纳：本题主要从正多边形的计算及等边三角形的性质为出发点，解题的关键是从图形中整理出直角三角形。首先通过旋转转化得到所需要的点E的位置，然后从图形中去解答问题。解决几何的最值问题常通过旋转构造出特殊的图案，如全等的三角形和等边三角形，或通过线段的旋转得出最短的线段。培养学生多观察、多思考，从旋转中找出规律，再利用学过的知识进行解题。

四、构造法

构造法是通过构建特殊图形解决问题的数学思维方法。利用已知的数学关系和理论作为思考工具，构建满足条件或结论的数学对象，可以清楚地反映出新构建的数学对象中原始问题的隐含关系和性质，这样就可以方便快捷地解决问题。在几何最值问题中，构造法仍然是解题思路中很常用的一种联想性方法。

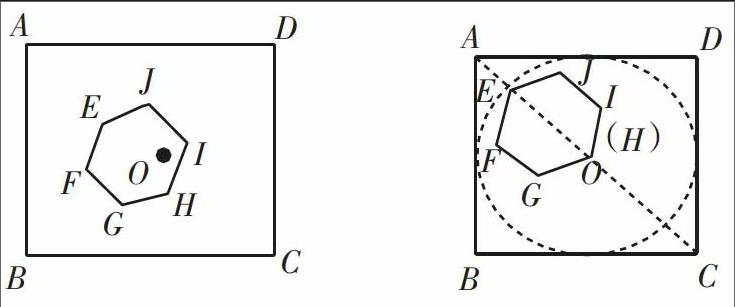
例5 （2015·浙江台州）如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个正六边形的边长最大时，AE的最小值为___。endprint

分析：当正六边形的边长最大时AE要最小，以点E为圆心，对角线EH为半径做与正方形ABCD相切的圆，点E在线段OA上，只需要求出OE和OA的值，就能够把问题解决。

解：要使得正六边形的边长达到最大，可以作正方形ABCD的内切圆⊙O，当⊙O的圆心O与六边形的H重合，且点E在线段OA上时，AE的长度最小，如右图：

归纳：本题主要考察的是正多边形与圆的问题，但是从图形中并没有发现有圆，这时只能构造一个内切圆，再利用内切圆的性质解决问题，构造内切圆解答本题的关键。

五、特殊位置法

将待解决的一般性问题，转化到特殊问题，一般问题的解答建立在这种特殊情形的基础上。

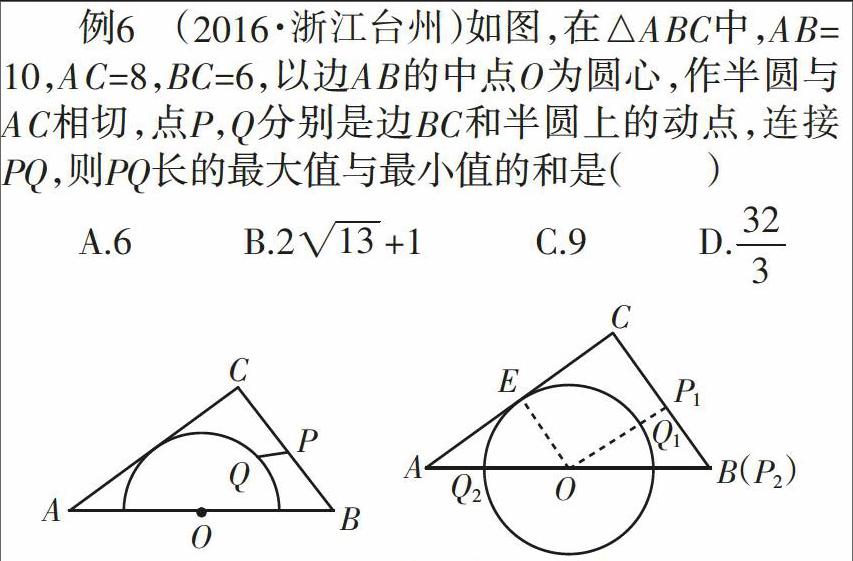
例6 （2016·浙江台州）如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动點，连接PQ，则PQ长的最大值与最小值的和是（）

分析：根据题目中所给条件可以得出△ABC的特殊性以及在△ABC里面的内切半圆的特殊性（如右图），这样的几何最值问题是建立在特殊性上面的，也是比较容易解决的，答案选C。

例7 （2017·浙江台州）如图，有一个不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组对边上，另外两个顶点B，D在正六边形内部（包括边界），则正方形边长a的取值范围是________

归纳：特殊位置法对于学生而言比较陌生，但是学生在解题的时候往往会忽略了图形的特殊位置，这说明他们知识的不牢固，定理运用的不够熟悉。在几何最值问题中多引导学生使用特殊位置法，也有助于学生对定理的熟练掌握，能够将难以理解的直观图形转化为自己熟悉的图形以及位置来解答。

台州近几年的数学中考都涉及了几何最值的问题，无论选择题还是解答题都有所分布，最值问题的大热也推动了数学思想的不断发展，对学生的逻辑思维能力具有促进作用。本文就台州近几年的中考最值题目研究几何最值问题的解题方法，希望对学生的几何最值问题解决有一定的帮助，对老师的教学也有促进作用。

参考文献：

1.李国敬.数形结合在初中数学教学实践中运用的研究.河南大学，2015.

2.金惠芬.解几何最值问题的方法[J].苏州教育学院学报，1998（01）：57-59+62.endprint