关于二维非对心碰撞角度的关系式推导

李 燕

(四川雅安职业技术学院，四川 雅安 625000)

关于二维非对心碰撞角度的关系式推导

李 燕

(四川雅安职业技术学院，四川 雅安 625000)

本文推导并讨论了表面光滑的非对心碰撞的角度问题,补充了教材关于碰撞问题这部分知识.

碰撞;非对心碰撞;恢复系数e

碰撞在日常生活及生产中随处可见,在研究微观分子或原子的运动时也会遇到碰撞问题.碰撞有两个明显的特点:一是碰撞物体间发生碰撞的时间极短,所以可只考虑碰撞物体间的冲力,而不考虑非冲力以外的力对物体的影响.二是虽然碰撞时间极短,但碰撞前后物体运动状态的改变却非常明显.正因有以上特点所以可方便我们应用守恒定律来研究碰撞问题,并且我们常常把碰撞物体模型化为球体.一般碰撞分为球的对心碰撞和球的非对心碰撞，如果两个小球碰撞前后它们的速度矢量都是沿着两球心的连线,则这样的碰撞就叫做“球的对心碰撞”或叫做“球的正碰”;如果两个小球碰撞前的速度矢量没有沿着两球心的连线,则这样的碰撞就叫做“球的非对心碰撞”或叫做“球的斜碰”.大多数物理教材在编写碰撞这部分内容时,一般只讨论了碰撞的速度变化和能量问题,没有强调关于非对心碰撞的角度问题.笔者在本文中推导并讨论了表面光滑的非对心碰撞的角度问题.

1 二维非对心碰撞角度的关系式推导

两小球碰撞前后速度矢量若在同一平面内,称为二维碰撞;碰撞前后速度矢量不在同一平面内,则称为三维碰撞.本文讨论二维碰撞.如图1所示质量为m1、初速度为v10的光滑小球和质量为m2、初速度为v20的光滑小球发生二维碰撞,碰撞后其速度分别为v1和v2(如图2所示),两球碰撞的恢复系数为e.为研究方便,可在两小球的速度矢量平面内建立直角坐标系O-xy,设两小球碰撞接触面的公切线方向为x轴,y轴沿碰撞时的联心线,如图2所示.

把两球看作一质点组,因外力矢量和为零,故动量守恒.根据动量守恒定律,在y轴方向上有

m1v10y+m2v20y=m1v1y+m2v2y.

(1)

碰撞时,因球面光滑,故两小球沿公切线方向即x轴方向不受力,所以碰撞前后两小球沿x轴方向的速度分量不变,有

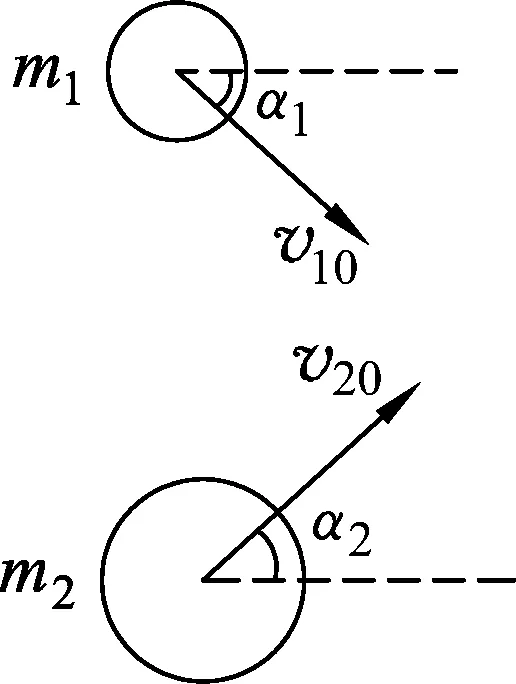
图1 小球碰撞前

v10x=v1x，v20x=v2x.

(2)

由恢复系数e的定义知对于材料一定的球,碰撞后分开的相对速度与碰撞前接近的相对速度成正比,故有

(3)

如图1和图2所示,若v10、v20与x轴的夹角分别是α1和α2;v1、v2与x轴的夹角分别是β1和β2,由(1)式得

m1v10sinα1+m2v20sinα2=m1v1sinβ1+

m2v2sinβ2.

(4)

由(2)式得

v10cosα1=v1cosβ1，v20cosα2=v2cosβ2.

(5)

由(3)式得

(6)

解以上(4)～(6) 3个方程,分别消去v1和v2得

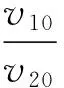
(7)

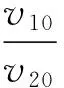
(8)

由(7)、(8)式消去v10、v20可得

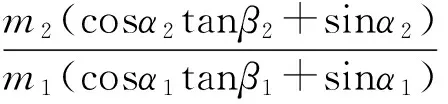
(9)

简化(9)式得

(10)

式(10)为二维非对心碰撞的角度的一般关系式.

2 关于二维非对心碰撞角度关系式的讨论

(1) 若两小球质量m1=m2,且它们初始状态都是运动的,当它们发生完全弹性非对心碰撞时(恢复系数e=1),式(10)简化为

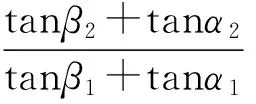
将上式两边交叉相乘进一步简化得

tanα1tanα2=tanβ1tanβ2.

(11)

(2) 若两小球质量m1≪m2,当恢复系数e=1时,可看作小球从倾斜方向与半径无穷大的球即光滑平面相碰撞,可把质量为m2的小球看作保持静止.由(10)式可得

etanα1=tanβ1.

(12)

分析:因为e=1,所以有α1=β1,即m1在m2的表面上作等角反射,如图3所示.

图3 图4

(3) 若两小球质量m1≪m2,当恢复系数0β1,如图4所示.即当两小球发生非完全弹性碰撞时,m1碰撞后速率减小了,出现了机械能的损失.

1 漆安慎,杜婵英.力学[M].北京:高等教育出版社,1998.

2 贾书惠, 李万琼. 理论力学[M].北京:高等教育出版社,2002.

2017-03-30)