常见国产制式手枪射击距离判断的一元线性回归分析

王宏伟， 尹丽兰， 季楷锋， 杨 军

(中国刑事警察学院痕迹检验系， 辽宁沈阳 110854)

常见国产制式手枪射击距离判断的一元线性回归分析

王宏伟， 尹丽兰， 季楷锋， 杨 军

(中国刑事警察学院痕迹检验系， 辽宁沈阳 110854)

运用线性回归理论建立了射击距离与射击残留物散布直径的一元线性回归方程，对几种常见手枪射击残留物的散布规律进行了研究。实验中，使用54式手枪、59式手枪、64式手枪、77式手枪、92式手枪各两把进行100发实弹射击实验，观察了5种手枪在垂直射击时射击残留物的散布直径与射击距离之间的关系。经分析计算得出实验中使用的5种常见手枪的射击距离与射击残留物散布直径均符合一元线性关系。

国产制式手枪； 射击残留物; 射击距离; 一元线性回归分析

0 引言

目前，对射击残留物的散布规律研究虽然已经有一些进展和实验数据，但通常只是就某一种枪痕迹的研究，内容较单一，研究成果远远不能满足复杂的刑事案件现场勘查的需要。本文基于已有的研究成果，对几种常见国产制式手枪在垂直射击时射击残留物散布直径的规律进行系统和全面的研究，可为涉枪案件侦查工作提供理论依据。通过测量射击残留物散布直径推测出射击距离。它对于准确判断案件的性质，分析作案人在现场的行为以及划定侦查的范围与方向具有一定的现实意义[1]。

1 射击残留物散布直径与射击距离间一元线性回归关系的建立

1.1 回归方程的建立

根据手枪射击残留物散布直径与射击距离关系，应用线性回归方程求得射击距离。对涉枪案件的侦破起到重要作用。

在某一范围内，手枪射击残留物的散布范围会随着射击距离的增加而扩大，两者之间的关系既复杂又密切，这种变量之间的相关关系被称为统计关系。线性回归关系就是用线性函数来近似的替代所研究的相关关系，并将所测得的每一个相对应点描绘在坐标上，若这些点在坐标上的位置与一条直线偏离不多，就可考虑采用线性回归；反之若这些点不在同一条直线上，就应使用多变量回归函数进行分析。由于实际测量中存在误差，这些点不会全部在一条直线上，如果这些点与线的偏距离越小，则这条直线的代表性就越好，这条直线被称为回归直线。

确定回归直线所根据的原则是使用所有观测数据误差的平方和达到极小值。若用(xi,yi)(i=1,2,3……n)表示一组观测数据，即n个观测点，则任意一条直线方程都可用下面方程表示：

y=ax+b

(1)

如果用这条线来表示射击残留物散布直径y与射击距离x的关系，则对每个已知的观测点(xi,yi)用同一横坐标xi的直线上的点(纵坐标为=ax+b)来替代实际值yi，其误差可表示如下：

δi=yi-i=yi-ax-b

(2)

由于用绝对值表示会给以后的数学处理带来麻烦，故常用每个误差的平方和作为总的误差，即

(3)

回归直线是在所求直线中误差平方和S最小的一条，即回归直线的系数a及常数b使S达到极小值。根据数学中的极值原理，要S达到极小值，(3)式中分别对a、b求偏微分，令它们等于0，于是a、b满足

(4)

(5)

即

(6)

则

(7)

整理可得

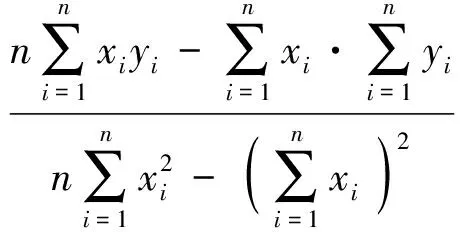
(8)

(9)

观察(8)、(9)式可知，计算a、b所需的量都可以从观测数据中得到，因此，回归直线方y=ax+b程便可以确定[2]。

1.2 相关系数与可靠性

在应用所求得的回归方程时，要注意不能把在某个条件下求得的回归线任意套用。变量x、y之间的线性关系密切程度可用相关系数r表示，r的表达式为：

(10)

r的值介于-1和1之间，其绝对值接近于1时，表明两变量之间线性关系紧密，当r=1时，表示两变量完全线性相关；当r=0时，表示两变量完全线性无关；当r>0时，表示两变量的变化趋势一致；当r<0时，表示两变量的变化趋势相反。

2 实验

2.1 实验器材

54式手枪、59式手枪、64式手枪、77式手枪、92式手枪；51式手枪弹20发、59式手枪弹20发、64式手枪弹40发、92式手枪弹20发；米尺；白色的确良布100张。

2.2 实验数据测量的方法

图1为实验数据测量图。实验中使用厘米刻度尺，以射击残留物较集中的区域为圆心，以能把大部分射击残留物包括在内的长度为半径画圆，得到半径R，通过R求出射击残留物散布直径y[3]。

图1 数据测量图

2.3 实验过程及结果

2.3.1 垂直射击

分别使用以上5种手枪在0 cm、5 cm、10 cm、20 cm、30 cm、40 cm、50 cm、60 cm、70 cm、80 cm、90 cm、100 cm距离进行垂直射击实验，在每个距离射击2次，测量射击弹丸的散布直径。以54式手枪为例，具体实验数据如表1所示。

54式手枪数据计算：

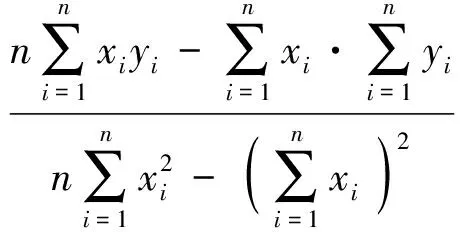
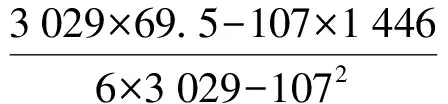
结果：y=0.223 9x+7.924 4

可靠性验证：

根据与54式手枪相同的方法计算得出其他枪支的线性回归方程及各自的可靠性验证如下：

54式手枪：y=0.223 9x+7.924 4，

可靠性r=0.981 9；

59式手枪：y=0.477 7x+6.897，

可靠性r=0.986 7。

64式手枪：y=0.214x+7.017 4，

可靠性r=0.980 6。

77式手枪：y=0.185 9x+8.018 6，

可靠性r=0.984 5。

92式手枪：y=0.433 2x+5.354 9，

可靠性r=0.991。

实验用5种常用手枪射击残留物散布直径y与射击距离x之间均符合一元线性回归关系[4]。

表1

2.3.2 验证实验

根据测得的数据分别求出a与b的值，得到弹丸散布直径y与射击距离x关系式，在已知某一值的情况下，通过关系式可求出另一值。

用5种常见手枪分别在同一地点且不知道射击距离的情况下对靶纸进行实弹射击，得到射击残留物散布直径y，通过y求出射击距离x。测得射击残留物散布直径分别为：

54式手枪y=16 cm；59式手枪y=24 m；64式手枪y=15 cm；77式手枪y=15 cm；92式手枪y=21 cm。

计算可得射击距离54式手枪x=36.5 cm；59式手枪x=35.8 cm；64式手枪x=37.3 cm；77式手枪x=37.5 cm；92式手枪枪x=36.1 cm。经实地测量射击距离为36.6 cm。

2.3.3 实验应用的讨论

回归方程的适用范围一般限于参照原始观测数据的变动范围，而不能随意外推，否则直线回归的假定成立将受到影响。

最佳现行回归关系是在10～40 cm范围内。因为射击残留物分布范围与射击距离有关系，近距离射击时，距离越近，喷射力越大，颗粒越集中残留物，分布范围越小；距离加大，子弹动能变小，颗粒分散50 cm后基本消失。如果火药颗粒比较密集，而且烟晕出现明显，说明射击距离在10 cm范围内。

如果在被射客体上测量得到残留物散布直径为y=19.8 cm，代入公式y=0.433 2x+5.354 9,可推算出射击距离x=13.93 cm。

在实验过程中，还要充分考虑测量工具、测量方法、测量精度、风速等多种因素的影响。

3 结论

(1)用54式手枪对白色的确良布进行射击试验,观测残留物散布半径与射击距离之间的关系。用数理统计进行回归分析得出射击距离x和射击残留物散布直径y的关系：y= 0.223 9x+7.924 4

(2)用59式手枪对白色的确良布进行射击试验,观测残留物散布直径与射击距离之间的关系。用数理统计进行回归分析得出射击距离x和射击残留物散布直径y的关系：y= 0.477 7x+6.897

(3)用64式手枪对白色的确良布进行射击试验,观测残留物散布半径与射击距离之间的关系。用数理统计进行回归分析得出射击距离x和射击残留物散布直径y的关系：y= 0.214x+7.017 4

(4)用77式手枪对白色的确良布进行射击试验,观测残留物散布直径与射击距离之间的关系。用数理统计进行回归分析得出射击距离x和射击残留物散布半径y的关系：y= 0.185 9x+8.018 6

(5)用92式手枪对白色的确良布进行射击试验,观测残留物散布直径与射击距离之间的关系。用数理统计进行回归分析得出射击距离x和射击残留物散布半径y的关系：y= 0.433 2x+5.354 9

用枪支近距离射击客体后,附着在客体上的射击残留物散布直径是可以测量的,将测量的数据代入上式中便可求出以上几种国产制式枪支在间距范围内的射击位置,准确揭示涉及此类枪支的枪击案件的现场情节和案件性质。

[1] 陈建华. 中国刑事科学技术大全—枪弹痕迹检验[M].北京:中国人民公安大学出版社，2002:78-79.

[2] 黄立宏.一元分析基础[M].北京:科学出版社，1998:7-8.

[3] 王放明.枪案物证分析新技术[M].长春:长春出版社,2004:31-32.

[4] 杨军，郭威. 枪弹痕迹学[M]. 北京：中国人民公安大学出版社, 2014：186-192.

(责任编辑于瑞华)

D918.91

王宏伟(1993—)，男，甘肃玉门人，2015级公安技术专业方向在读研究生。研究方向为枪弹痕迹检验。