差分进化下的二级圆柱齿轮减速器优化设计
◎顾嘉
差分进化下的二级圆柱齿轮减速器优化设计
◎顾嘉
本文在构建二级圆柱齿轮减速器数学模型的基础上,浅析了差分进化下的二级圆柱齿轮减速器优化,差分进化法有利于实现二级圆柱齿轮减速器尺寸的减小,实现二级圆柱齿轮减速器制造成本的大幅度降低,对于拓展二级圆柱齿轮减速器的应用市场具有至关重要的意义。本文通过对差分进化下的二级圆柱齿轮减速器优化设计进行分析,已经为我国二级圆柱齿轮减速器的优化设计提供借鉴。
二级圆柱齿轮减速器在诸多工业领域得到了广泛应用,诸如工矿企业、运输企业以及建筑部门等。传统的二级圆柱齿轮减速器优化设计,大多采用手动迭代方法,或者是采用计算机语言,其优化模型具有高维特点,且呈线性非凸与多约束特征。传统的二级圆柱齿轮减速器优化设计方法具有庞大的计算量,且计算极为繁琐,无法取得理想的优化效果。一般情况下,二级圆柱齿轮减速器的安装空间容易受场合限制。因为,为满足二级圆柱齿轮减速器的承载要求,延长其使用寿命,增强其可靠性,有必要立足于二级圆柱齿轮减速器的结构尺寸和实际体积进行优化设计。
构建数学模型
下图1是二级圆柱齿轮减速器结构图,如图所示,二级圆柱齿轮减速器的输入功率为6.2kW,其高速转轴的转速设置为1450r/min,其总传动比是31.5,其齿轮因素为0.4。该图中的二级圆柱齿轮减速器的大齿轮采用45号钢,其正火硬度,在187HB到207HB之间;小齿轮采用45号钢,其调质硬度在228HB到255HB之间。该图中的二级圆柱齿轮减速器至少要保持十年以上的工作年限。建立目标函数。建立如下目标函数:
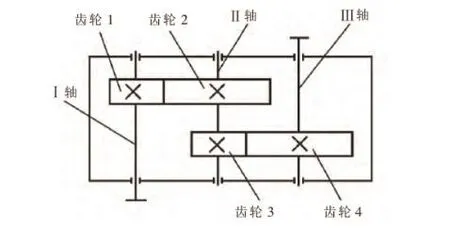
图1 二级圆柱齿轮减速器结构图
F(X)=a =a1+a2=[mn1z1(1+i1)+mn2z3(1+i2)]/(2cosβ)在该目标函数中,二级圆柱齿轮减速器具有最小体积和总中心距,且具有最为紧凑的结构和最轻的质量。在该目标函数中,“a”代表的是总中心距,“ a1”代表的是高速级中心距,“a2”代表的是低速级中心距,“mn1”代表的是高速级齿轮法面模数,“mn2”代表的是低速级齿轮法面模数,“ i1”代表的是高速级传动比,“i2”代表的是低速级传动比,“z1”代表的是高速级小齿轮齿数,“z3”代表的是低速级小齿轮齿数,“β”代表的是齿轮螺旋角。
确立设计变量。对总中心距“α”的计算涉及诸多独立参数:mn1、mn2、z1、z3、i1、β等。因此,取如下设计变量:

确认约束条件。按照渐开线齿轮承载能力法则进行齿轮计算,必须确保齿轮同时满足如下条件:(1)齿根弯曲疲劳强度条件。(2)齿面接触疲劳强度条件。具体要做到如下几点:对设计变量的上下界限进行确认,取14≤z1≤22;16≤z3≤22;2mm≤ mn1≤ 5mm;3.5mm≤ mm2≤6mm;5.8≤i1≤7;8°≤β≤15°。对应的6个不等式约束条件如下:2≤x1≤5;3.5≤x2≤6;14≤x3≤22;16≤x4≤22;5.8≤x5≤7;8≤x6≤15。上述不等式表明,要想保持齿轮传动平衡,不宜使轴向力过大,要对短期过载进行适应,确保高速级和低速级大齿轮基本上保持一致的浸油深度,要确保轴齿轮具有适中的轮分度圆尺寸。另外,要对齿面弯曲强度条件进行确认如下:
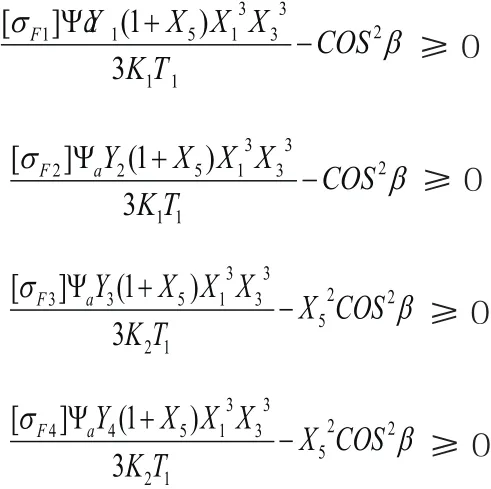
在上述式子中,[σF1]代表的是齿轮1的许用弯曲应力;[σF2]代表的是齿轮2的许用弯曲应力;[σF3]代表的是齿轮3的许用弯曲应力;[σF4]代表的是齿轮4的许用弯曲应力。“Y1”、“Y2”、“Y3”、“Y4”分别代表齿轮1、齿轮2、齿轮3、齿轮4的齿形系数。此后,还要对齿面接触强度条件进行确认,高速级齿面接触强度条件如下:
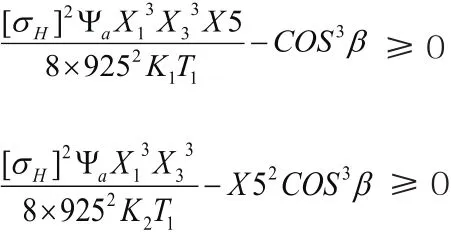
在上述式子中,“[σH]”代表的是许用接触应力;“ T1”代表的是高速Ⅰ轴以及中间轴的转矩;“ T2”代表的是高速Ⅱ轴和中间轴的转矩。“K1”代表的是高速级的载荷因数;“T2”代表的是低速级的载荷因素。最后,对几何约束的条件进行确认:a2-E-De2/2≥0。其中,“E”代表的是低速级轴线和高速级大齿轮齿顶圆二者之间的距离。“De2”代表的是高速级大齿轮的齿顶圆的直径。
差分进化下的二级圆柱齿轮减速器优化
差分进化。(1)变异操作:在群体内对个体进行随机选择,将之作为基本向量,另外两个个体作为差向量,实现对突变个体的获取。(2)交叉操作:在第一个变异产生的个体与第一个种群个体之间进行交叉操作,得出试验个体。(3)选择操作:DE选择通常是一对一的,该选择在实验载体与原始群体的个体间进行。
参数优化。如下图2所示,使用ADE算法,取NP(种群规模)=100,取CR(交叉概率)=0.9,取Gmax(最大进化代数)=1000,F(缩放因子)=2e[1-Gmax/(Gmax+1-g)]。对a(总中心距)进行最小值的优化。
优化参数:

综上所述,在确保二级圆柱齿轮减速器承载能力的基础上,对其结构参数进行优化设计。其优化设计结果表明,差分进化下的二级圆柱齿轮减速器优化设计,能实现减速机尺寸的大幅度减小,有利于二级圆柱齿轮减速器制造成本的有效降低,有利于拓展二级圆柱齿轮减速器应用市场的范围。差分演化算法能通过对动态缩放因子的利用,实现用户参与程度的有效降低。同时,对收敛速度进行充分考虑,有效避免对局部以及全局最优解能力的获取。
(作者单位:伟泰科技股份有限公司)

