粗糙集属性约简方法研究

赵昶宇

（天津津航计算技术研究所，天津 300308）

粗糙集属性约简方法研究

赵昶宇

（天津津航计算技术研究所，天津 300308）

为了提高属性约简的准确率和工作效率，使其能够处理不相容和不确定关系的信息系统，提出了一种粗糙集属性约简方法。首先，将属性的重要性度量作为启发式信息；然后，引入遗传算法快速找到条件属性集合中适应值最好的个体作为遗传的优化解集合；最后，使用遗传算法生成初始信息素，利用蚁群算法的局部寻优和正反馈机制得到粗糙集属性约简的最优解。

属性约简；粗糙集；遗传算法；蚁群算法

在实际应用中，对粗糙集属性约简的研究有非常重要的意义——化简冗余属性，保留最佳决策，大大提高数据的处理效率。利用粗糙集理论和约简方法可以实现知识获取、机器学习、图像处理、决策制订、模型建立等应用。高效的约简方法是将粗糙集理论应用于数据挖掘与知识发现领域的基础。Wong S.K.M.和Ziarko在1985年已经证明了一个信息系统或决策表的最小约简是一个NP-hard问题，这是由数据组合爆炸引起的，不存在统一、规范的高效方法。对于大型数据库，最小约简事实上并不存在，得到的只是近似约简。为了研究更有效的约简方法，有效地获取较优的属性约简，并降低实现的时间复杂度，寻求快速的约简方法是目前粗糙集理论的主要研究课题之一。

目前，最常见的粗糙集属性约简方法有以下几种：①基于区分矩阵的属性约简算法。该算法直观，易于理解，但是，在处理大量数据集合时，算法的时间复杂度和空间复杂度成指数增长，约简速度非常慢。②基于属性依赖度的约简算法。该算法在对大量数据集合进行约简时，效率比较高，但是，该算法只得到了条件属性的核，并没有得到属性的一个约简，且不适合不相容系统的约简。③基于属性重要度的约简算法。该算法与基于属性依赖度的约简算法相比，能够更好地处理属性满足确定性关系，且有强烈因果关系的属性集。但是，该算法并不能保证一定能够找到信息系统的最优解。④基于遗传算法的属性约简算法。遗传约简算法大大提高了决策表约简结果的准确性和算法的高效性，但是，该算法不能够处理不相容和不确定关系的信息系统。

为了改善粗糙集属性约简方法的不足之处，提高属性约简的准确性和效率，处理不相容和不确定关系的信息系统，本文提出了一种粗糙集属性约简的方法。

1 利用遗传算法得到条件属性的优化解

1.1 信息系统与决策表

信息系统是粗糙集理论中的研究对象，即I＝（U，A，V，f）.其中，U为论域，即所有研究对象的集合；A为研究对象属性的集合；V为研究对象属性值的集合，V＝∪a∈AVa，Va是属性a∈A的值域；f为信息函数，f：U×A→V为单一映射，即f（x，a）∈Va，它指定U中每一对象的属性值。对于信息系统I＝（U，A，V，f），如果研究对象属性集合A由条件属性C和决策属性D组成，即A＝C∪D，C∩D＝Ф，则此时信息系统I称为决策表。

1.2 属性约简和值约简

令R为一等价关系族，且r∈R，当ind（R）＝ind（R－{r}），称r为R中可省略的；否则，r为R中不可省略的。当任意一个r∈R，如果r不可省略，则称族R为独立的。显然，当R为独立的，且PR，则P也是独立的。P中所有不可省略关系的集合被称为P的核，记作core（P）。

值约简是对决策表的一种简化，决策表中一条实例可以看作一条规则，其中可能包含冗余属性值，因此，对实例属性值的约简就是对决策规则的约简。决策规则的约简是分别消去每个规则的不必要条件，它不是整体上的约简属性，而是针对每个决策规则，去掉表达该规则时的冗余属性值，以便进一步使规则最小化。

1.3 遗传约简算法

1.3.1 染色体编码

采用长度为N的二进制串来表示一个个体，即被选中的条件属性表示为“l”，不被选中的条件属性表示为“0”.

1.3.2 确定初始种群

种群的初始化是遗传算法的关键，用传统的遗传算法确定初始种群时，多半采取随机生成法形成染色体方案，以致于迭代开始就可能形成许多不可行的方案，要进行大量的计算后才能得到优化的方案，这在很大程度上降低了算法的运算效率。本文改进传统遗传算法，改进后能够降低随机产生的种群初始值的盲目性，提高算法的效率。改进后的初始种群的产生方式是：利用属性核本身的特征，即属性核是所有属性约简的交集，限制初始种群。由于每一种属性的约简都包括了属性核，因此，在每个染色体中，将属性核所在的位置上的基因强制取值为“1”.

1.3.3 建立适应度函数

由属性约简的定义可知，个体的适应度主要取决于2个方面，即所含条件属性的个数（应该尽量少）和区分能力（应尽量强）。因此，定义适应度函数为：F（v）＝|C|-Lv.其中，|C|为条件属性集中属性的个数；Lv是个体中所包含的条件属性的个数。

1.3.4 判断是否满足终止条件

算法终止条件是，当连续繁殖很多代的最优条件属性的适应值没有变化时，算法停止，否则转步骤1.3.5.

1.3.5 选择算子

由于操作简单，传统的遗传算法大多采用“轮盘赌”选择算子。但是，这个方法一方面容易导致局部最优而无法进化；另一方面，无法体现个体优劣，导致搜索精度不够。

本文对传统遗传算法的“选择算子”进行改进，改进后的选择方式可确保适应度比平均适应度大的一些个体一定能够被遗传到下一代群体中，所以，该方法的选择误差比较小。具体操作如下：①设条件属性集合的长度为N，每个属性的适应度为Fi（i＝1，2，…，N），计算条件属性集合中每个属性在下一代条件属性集合中的期望生存数目，即②用Ni的整数部分确定各个对应条件属性在下一代条件属性集合中的生存数目。其中大于Ni的最大整数，这样可以确定下一代条件属性集合中为各个条件属性新的适应度，用“轮盘赌”选择算子，随机确定下一代条件属性集合中还未确定的个条件属性。

1.3.6 交叉算子

常用的交叉方式有一点交叉、两点交叉、多点交叉和一致交叉等。本文对遗传算法进行改进，采用多点位单基因交叉的方式，用父代最优解Tmax与子代染色体池进行交叉操作。该方法能够避免算法过早地丧失进化能力，具体步骤如下：①在染色体池T中选择进行交叉操作的条件属性集合Ti和属性约简的最优解Tmax；②随机生成交叉片段和交叉区域；③将Ti的交叉区域加到Tmax前面，将Tmax的交叉区域加到Ti前面；④删除与交叉区域相同的条件属性，得到2个新的条件属性集合。

1.3.7 变异算子

采用基本位变异算子，其具体执行过程是：对于条件属性的每一个基因（二进制的0或者1），根据变异概率指定其为变异点。对于每一个指定的变异点，条件属性核对应的基因位不发生变异，其他则对其基因值做取反运算，从而产生出一个新的条件属性集合。

1.3.8 复制算子

在得到新一代条件属性集合之后，如果其中最坏的属性集合（适应值最小）的适应值小于上一代最好的属性集合（适应值最大）的适应值，则用上一代最好的属性集合代替新一代最坏的属性集合。该方法确保算法收敛。

2 利用蚁群算法得到粗糙集属性约简的最优解

因为蚁群算法在初始时刻比较缺乏信息素，导致寻优速度不理想。因此，先使用上述遗传算法生成初始信息素，提高初期求解的运行速度。

遗传算法的求解结果向蚁群算法信息素的转化过程是：选取遗传算法终止时条件属性集合中适应值最好的10%的个体作为遗传的优化解集合，以从剩余可选条件属性中选择属性i的概率作为蚁群算法初始信息素的一部分。初始所有属性之间的信息素的浓度τ初始为：

式（1）中：x为优化解集合中属性j选择属性i的总次数；y为优化解集合中解的个数；ηi为属性i对属性j的重要性。改进的蚁群算法描述如下：①将m个蚂蚁分别置于n个属性节点上，利用遗传算法得到初始所有属性之间的信息素，并设定最大迭代次数。②如果有蚂蚁成功地将属性i添加到属性集合中，则为属性节点间的信息素浓度赋予增量Δτi＝Ce×K；否则，如果属性i未被添加到属性集合中，则为属性节点间的信息素浓度赋予增量Δτi＝Cp×K.其中，K为选择属性所用的时间开销；Ce和Cp为相应的奖惩因子。③更新所有属性节点之间的信息素τi（t），即τi（t）＝τi（t）＋Δτi，其中，i＝1，2，…，n.④在属性约简中，下一个属性的选择只能由已经选择的属性来决定。设Rk为已选属性的集合，k为迭代次数，i为已选属性，j为待选属性。根据各个属性之间的信息素分布情况，计算蚂蚁在Rk为已选属性集合的情况下，从剩余可选条件属性中选择属性j的概率P（j|Rk）.基于得到的最大概率值为每只蚂蚁分别选取下一个属性。⑤根据所有蚂蚁选取的属性，计算对应的目标函数F（v），输出F（v）的最大值及其所对应的属性集合，即最小约简。⑥如果达到最大的迭代次数，或者迭代出现退化现象，则当前得到的最优解即为所得的属性集合的最小约简；否则，清空所有蚂蚁的蚁集，跳转到步骤②。从剩余可选条件属性中选择属性j的概率P（j|Rk）的公式是：式（2）中：集合U为第k次迭代后剩余可选条件属性；τij为属性节点i到属性节点j的路径信息素浓度值；ηij为属性j对属性i的重要性；α为2个属性节点（i，j）之间的信息素浓度值的权重；β为属性j对属性i的重要性的权重。

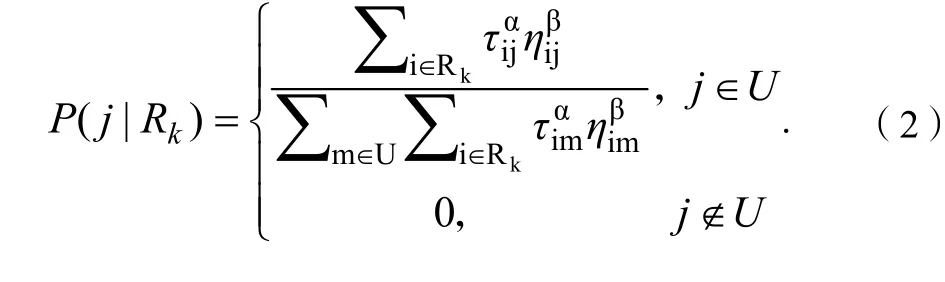
3 结束语

为了提高属性约简的准确性和效率，且能够处理不相容和不确定关系的信息系统，本文提出了一种粗糙集属性约简的方法。

该方法将属性的重要性度量作为启发式信息，引入遗传算法快速找到条件属性集合中适应值最好的个体作为遗传的优化解集合，然后使用遗传算法生成初始信息素，利用蚁群算法的局部寻优和正反馈机制得到粗糙集属性约简的最优解。

本文提出的属性约简的方法在加强局部搜索能力的同时，保持了全局寻优的特性，既保证了所求约简含有比较少的属性，又保证了分类质量，能够获得最佳的搜索效果。另外，该方法缩短了属性约简的计算时间，并提高了决策表属性约简结果的准确性。

［1］闫德勤，王杨.基于关联矩阵的属性约简算法［J］.计算机工程与应用，2005，41（20）：181-182.

［2］刘少辉，盛秋戬，吴斌，等.Rough集高效算法的研究［J］.计算机学报，2003，26（05）：524-529.

［3］周献中，黄兵.基于粗糙集的不完备信息系统属性约简［J］.南京理工大学学报，2003，27（5）：630-635.

［4］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999：146-254.

［5］梁云川，李德玉.基于子集类蚁群模型的属性相对约简算法［J］.计算机科学，2008，35（11）：147-150.

TP18

A

10.15913/j.cnki.kjycx.2017.20.013

2095－6835（2017）20－0013－03

赵昶宇（1982—），男，陕西汉中人，工学硕士，高级工程师，主要从事嵌入式系统软件测试方面的研究。

〔编辑：白洁〕