中国开放式股票型基金的风险偏好特征

白雪　牛锋

摘要：基于多种数据生成方式全面检验了核正则化最小二乘法（KRLS）的样本拟合效果和样本外预测能力，在此基础上使用KRLS方法对传统定价模型进行修正，分析我国四种类型开放式股票型基金的风险偏好特征。研究发现：与广义线性模型相比，KRLS方法能够有效捕捉随机变量之间复杂的非线性相关关系。从横截面维度来看，我国不同风格的基金均偏好于投资高市值股票，其中指数型基金的投资比例最高；除成长型基金外，价值型和平衡型基金也均热衷于投资“成长型”股票。从时间维度来看，我国指数型基金的风险偏好相对稳定，而三类主动型基金表现出明显的风险调整行为，并且风险偏好的变化特征较为相似。

关键词：基金风格；风险偏好；风险调整；KRLS

中图分类号：F224；F830.9文献标识码：A文章编号：10037217（2017）05004607

一、引言

一般来说，基金风格反映基金管理者投资过程中的总体风险状况，能够作为投资者和监管部门进行风险管理的基础。然而，由于基金经理人与投资者之间的委托代理问题，基金经理通常会采取主动的风险调整策略。基金宣称的投资风格能否反映其真实的风险偏好，各种类型基金在面临不同的金融市场环境时会做出怎样的风险调整等问题一直是学术界和实务界的关注热点。

现有文献大多基于多因素模型考察投资基金的风险溢价，以此判断基金经理人投资过程中的风险偏好。但是金融资产超额收益与风险因子之间通常具有非线性、非可加的复杂相依关系，传统多因素模型的线性假设并不成立[1]。虽然部分文献通过引入高阶项等方法对传统定价模型进行了改进[2]，但仍无法克服定价模型在形式设定上存在的主观性。为了克服传统定价方法在模型设定等方面存在的缺陷，本文将核正则化最小二乘法（Kernel Regularized Least Squares，KRLS）引入金融研究领域，并基于多种数据生成方式对KRLS的有效性进行全面检验。在此基础上，使用KRLS方法对传统定价模型进行修正，从多个维度考察我国开放式股票型基金的风险偏好特征。

本文的主要贡献体现在以下几个方面：研究内容上，一方面，我们从横截面维度和时间维度两个层面考察了不同类型基金的风险偏好特征，有助于认清我国开放式股票型基金的总体风险偏好和变化趋势；另一方面，分析了基金投资风格与其真实风险偏好的关系，这对把握基金的真实风险状况、完善证券投资基金监管具有重要的现实意义。研究方法上，将KRLS方法引入到金融研究领域，对传统的定价模型进行修正，不仅考察了风险因子对超额收益的平均影响，还对投资基金逐点的风险偏好加以分析，这在一定程度上弥补了传统模型的局限性。

二、文献综述

基金的投资风格是判断其风险偏好以及风险投资行为的重要基础。然而，大量的研究文献表明许多因素会导致基金的投资风格和风险偏好发生改变，从而使基金发生投资风格漂移现象[3，4]。王敬和刘阳发现历史业绩对基金的投资风格持续性具有一定影响[5]。艾洪德和刘聪、肖继辉和彭文平发现基金经理的教育经历、从业经验等个人特征与基金的投资风格漂移倾向显著相关[6，7]。

除既定的投资风格外，基金行业锦标赛、基金经理职业忧虑等多种因素都会对基金的投资风险偏好产生影响。Brown等首次将锦标赛理论引入基金行业，指出前期业绩较差的基金经理人倾向于在后期提高投资风险[8]。此后，这一理论得到众多学术研究的支持[9，10]。罗真和张宗成认为基金经理的职业忧虑水平会对基金投资风险产生显著影响[11]。刘莎莎等从委托代理问题等方面概况了基金经理调整投资风险的动机[12]。此外，金融市场环境同样会对基金的投资风险产生影响[13]。

鑒于诸多因素会影响基金的投资风险偏好，国内外众多学者围绕基金的投资风格以及投资风险行为展开了广泛研究。目前来看，识别基金的投资风格、考察基金风险偏好的方法众多，其中多因素模型的应用最为广泛。Fama和French通过市场资产组合、市值因子和账面市值比因子对股票的超额收益进行解释，该三因子模型在解释金融资产的横截面收益上得到了广泛应用[14]。随后，学者对三因子模型进行了拓展，如Carhart构建的加入动量因子的四因子模型、Fama和French提出的五因子模型等[15，16]。然而，现有的多因素模型通常基于线性假设考察金融资产超额收益与不同风险因子之间的关系，因而存在一定的局限性。

传统的多因素模型不能捕捉风险偏好的时变性和不同风险因子之间的交互影响，为此许多学者对多因素模型进行了拓展研究。如Olmo和Pouliot基于变点检验考察了基金绩效以及风险承担的动态变化[17]。随后，Bandi和Renò使用半参数扩散模型研究了金融变量之间复杂的非线性关系，但是，这一方法由于模型的局限性难以在资产定价中得到广泛应用[18]。为了解决模型的设定难题，Rifkin等基于机器学习算法提出正则化最小二乘法，这一方法无需对模型形式进行事前假定，能够兼顾模型的灵活性和简洁性[19]。此后，Hainmueller和Hazlett将Gaussian核函数应用到正则化最小二乘法中，不仅有效解决了模型设定的难题，还对估计系数构造了相应的假设检验[20]。

综上所述，诸多因素可能导致基金的风险偏好偏离既定的投资风格，为了确定不同类型基金的总体风险状况，需要对基金的风险偏好特征进行多维度的考察。目前利用收益率研究基金风险偏好的文献广泛使用基于相关性的回归方法，但这类方法依赖于模型形式的正确设定，模型设定的偏误会影响估计结果的无偏性和有效性。而核正则化最小二乘法（KRLS）无需对模型形式进行事先假定，且可以同时考察基金的平均风险偏好和逐点的风险偏好特征，为考察多维数据的相依结构提供了灵活准确的处理方法。

因此，本文首先对KRLS方法的模型构建和参数选择进行详细阐述，并利用多种非线性相关关系的随机样本数据检验KRLS方法的样本拟合效果和样本外预测能力，以证明KRLS方法的有效性。在此基础上，使用KRLS方法对传统定价模型进行修正，进而从多个维度考察我国开放式股票型基金的风险偏好特征。endprint

三、研究设计

（一）样本及数据

本文选取我国开放式股票型基金作为研究样本，研究区间为2010年1月1日到2015年6月30日。根据各个基金公示的投资风格、投资策略和投资目标，将投资基金划分为成长型、平衡型、价值型和指数型四类。最终得到的样本包含161只成长型基金、34只平衡型基金、43只价值型基金、63只指数型基金。基金收益率为根据复权单位净值计算的对数收益率，不同风格的基金指数收益根据各基金收益率等加权平均得到。此外，本文使用FamaFrench三因子模型中的市场风险因子（MKT）、规模风险因子（SMB）和价值风险因子（HML）考察基金的风险偏好特征。为了降低其他“噪声”对基金收益率的干扰，基金收益率和风险因子均采用周频数据。

财经理论与实践（双月刊）2017年第5期

2017年第5期（总第209期）白雪，牛锋：中国开放式股票型基金的风险偏好特征——基于核正则化最小二乘法的分析

（二）基于KRLS的定价模型

KRLS模型通过一个对称、正定的核函数（Kernel Function）衡量不同观测点之间的相似程度，进而能够对风险因子与超额收益之间的复杂相关关系进行拟合。假定（yi，xi）为一组样本观测数据，其中i=1，2，...，N，xi∈RD表示D维自变量，即风险因子，yi∈R为对应因变量，即基金超额收益。Gaussian核函數的形式如式（1）所示：

k（xi，xj）=exp（-‖xi-xj‖2σ2） （1）

其中，exp（·）为指数函数，‖xi-xj‖为自变量xi与xj的欧氏距离，σ2为Gaussian核函数的窗宽（Bandwidth）。

自变量观测值之间的欧氏距离越小，Gaussian核函数的值越大，对应的样本点之间的相似程度越高。对于任意给定的自变量x*，f（x*）的取值可以表示为各观测值与x*相似程度的线性函数，如式（2）所示：

f（x*）=c1k（x*，x1）+c2k（x*，x2）+…+cNk（x*，xN）（2）

其中，ci为各观测值对应的权重，k（x*，xi）为Gaussian核函数。可以看出，观测值与x*越相似，对x*处因变量预测值的影响越大。使用类似方法，可以得到任意自变量x对应的f（x）预测值。这样，我们可以基于“相似程度”将定价模型的方程形式f（x）表示为：

f（x）=∑Ni=1cik（x，xi）（3）

由式（3）可以看出，KRLS模型假定变量之间的相关信息蕴含在观测值的“相似程度”中，风险因子的取值越为“相似”，对应的超额收益应当越为接近。为了书写方便，将式（3）的定价函数由式（4）所示的矩阵形式表示：

y=k（x1，x1）k（x1，x2）…k（x1，xN）k（x2，x1）k（xN，x1）…k（xN，xN）c1c2cN=Kc （4）

（三）模型求解及参数设定

为了对样本数据进行拟合，需要对不同观测点的权重c进行估计。权重c的选择应当满足以下两个条件：一方面，拟合方程应当使预测偏误的平方和最小；另一方面，为了避免过度拟合，估计方程应当尽量平滑简单。这里，在目标函数中加入正则项，通过式（5）所示的最小化问题得到最为合适的权重向量c*。

minf∈H ∑i（V（f（xi），yi）+λR（f））（5）

其中，V（f（xi），yi）为损失方程，表示拟合方程对于各观测点的估计偏误。R表示“正则化项”，用来对拟合方程的复杂程度施加惩罚。λ为模型参数，控制着模型求解中对于拟合偏误和模型复杂程度的权衡。

与线性模型相似，式（5）中的损失方程V可以用∑i（f（xi）-yi）2=（y-Kc）T（y-Kc）衡量。此外，我们采用Tikhonov提出的正则化方法[21]，使用‖f‖2K=∑i∑jcicjk（xi，xj）=cTKc作为模型复杂程度的“惩罚项”R（f）。式（5）所示的最优化问题可以表示为：

minc∈RD （y-Kc）T（y-Kc）+λcTKc （6）

c*=（K+λI）-1y （7）

给定核函数窗宽σ2以及正则化参数λ时，对（6）中目标方程的一阶条件进行求解，能够得到式（7）所示的权重c的最优解。这样，通过y*=Kc*能够得到任意自变量对应的因变量的条件期望。

为了得到式（7）所示的最优权重c*，需要对核函数窗宽σ2以及正则化参数λ进行设定。其中，核函数中的窗宽σ2控制着对“相似程度”进行判断的尺度，合适的窗宽应当能够对样本点是否相似进行有效界定。我们使用Hainmueller和Hazlett的方法[20]选择合适的窗宽。正则化参数λ控制着模型求解中对于拟合偏误和模型复杂程度的权衡，借鉴Hastie等的研究，根据“留一误差”（LeaveOneOut Errors）方法选择合适的λ[22]。

（四）基金的风险特征分析

根据y*=Kc*能够得到给定风险因子数值条件下基金超额收益的条件期望，为了分析基金的风险偏好，根据式（3）计算单个自变量对应的偏导数，考察各风险因子对基金超额收益的边际影响。假定自变量X=（x1，…xd，…xD），自变量在风险因子xdj处对应的逐点偏导数可以表示为：

yxdj=-2σ2∑iciexp-‖xi-xj‖2σ2（xdi-xdj）（8）

分别计算逐点偏导数在各个样本点处的取值，可以得到风险因子xd对超额收益y的平均边际影响，如式（9）所示：

ENyxdj=-2σ2N∑j∑iciexp-‖xi-xj‖2σ2（xdi-xdj）（9）

式（9）所示的样本平均偏导数含义与FamaFrench三因子模型中的类似，表示其他自变量不变时，某一风险因子变动一单位对超额收益的平均影响。endprint

四、模拟结果

（一）KRLS的拟合效果

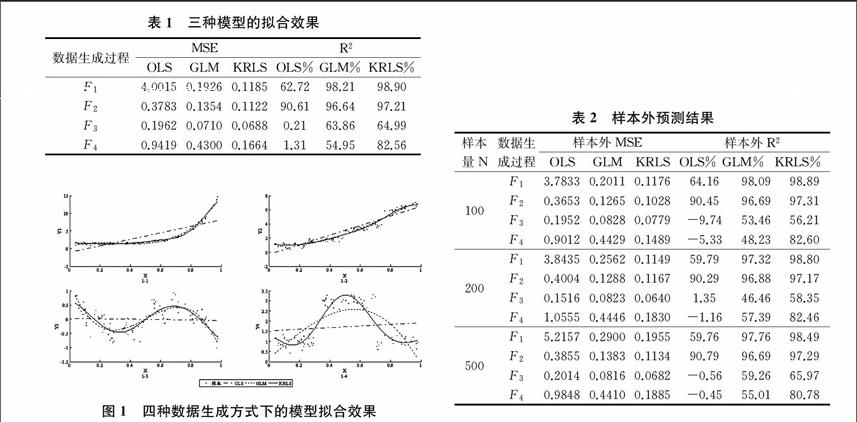
为了对KRLS的样本拟合效果进行直观分析，我们基于四种常见的非线性相依关系（F1，F2，F3和F4）生成样本数据，分别模拟指数型、结构突变型、三角函数型以及跳跃型相依关系；在此基礎上，分别使用OLS模型、广义线性模型以及KRLS方法对模拟数据进行拟合。图1为三种模型的样本拟合效果。

可以看出，由于数据的真实相依结构不满足线性假定，传统的OLS方法难以捕捉自变量和因变量之间真实的相关关系。在F1和F2两种数据生成过程下，GLM能够在一定程度上刻画因变量的非线性变化趋势。但是由于受到模型形式限制，广义线性模型对变量的非线性变化不够敏感。而KRLS方法由于不需要对模型形式进行事先假定，能够更加准确地捕捉变量的非线性变动，当变量间的非线性关系较为复杂时，这一优势表现更为明显。

图1-1、1-2、1-3、1-4分别对应四种数据生成过程，F1：y1=exp（5*（x-0.25）2）+05*exp（x-05）+ξ；F2：y2=1+2*int（x/025）*x+ξ；F3：y3=02*sin12πx+05*cos3πx+ξ；F4：y3= 1+2*I（03

表1报告了不同数据生成方式下三种模型的均方误差（MSE）和拟合优度（R2）。可以看出，三种模型中，OLS模型对四种非线性样本拟合的均方误差（MSE）均明显较高；即便在加入自变量的高阶项之后，GLM对应的均方误差仍高于KRLS。这一结果表明，核正则化最小二乘法对样本数据的拟合效果最佳。根据拟合优度系数能够得到相似的结论，KRLS方法对四种类型数据的拟合优度系数均最高。

注：样本量N=100。

（二）样本外检验

为了提高模型的预测能力，KRLS在目标函数中加入正则项对模型的“复杂程度”施加惩罚，从而保证拟合曲线的平滑性。我们利用四种数据生成方式得到模拟样本，取其中50%的样本观测值估计模型，使用估计模型对剩余50%的样本点进行预测，从而得到样本外预测的均方误差（MSE）和拟合优度（R2）。表2报告了样本量分别为100、200和500时三种模型的样本外预测结果。

可以看出，在不同的样本容量下，使用OLS模型得到的样本外MSE均较高，相应的样本外R2也低于另外两类模型。对于GLM和KRLS模型，当样本容量较小（N=100）时，广义线性模型在四种数据生成方式下的样本外MSE均大于KRLS模型；根据样本外R2得到的结论基本一致，四种数据生成方式下KRLS模型的样本外预测R2均大于GLM模型。随着数据生成样本的不断增大，这一结论始终成立，说明核正则化最小二乘法具有较强的样本外预测能力。

五、实证分析

（一）描述性统计

表3中四种基金指数收益率的描述性统计结果显示，我国四种风格的基金指数收益均为正，说明研究区间内基金净值总体呈上升趋势。其中，指数型基金平均收益最低，但波动幅度却最大。其他三类基金中，价值型基金的平均收益较高，成长型基金的平均收益最小；从标准差以及极端分位点信息可以看出，价值型基金的波动幅度较高，成长型基金次之，而平衡型基金的波动最小。此外，相应的JB检验显示，成长型、平衡型和价值型基金指数收益接近服从正态分布，而指数型基金指数收益率分布存在明显的“尖峰厚尾”特征。

注：表中收益率的单位为%；Q_10%和Q_90%分别表示收益率的10%和90%分位点；*、**和***分别表示在10%、5%和1%的水平下显著。

（二）基金的平均风险偏好

Fama和French提出的三因子模型将单个资产的超额收益表示为市场风险因子（MKT）、规模因子（SMB）和价值因子（HML）的线性形式[14]。由于超额收益与风险因子之间的关系可能是非线性的，并且具有复杂的交叉效应，因此我们使用KRLS模型对基金指数超额收益与风险因子之间的关系Rit=f（MKTt，SMBt，HMLt）进行拟合，进而反推各风险因子对超额收益的边际影响。

表4为相应的实证结果。可以看出，四种风格基金对应的R2均超过94%，说明FamaFrench三因子能够对四种风格基金的超额收益进行很好的解释。从不同风险因子来看，四类基金的市场风险因子（MKT）系数均较高，并且在1%的水平下显著，说明各类基金均具有显著的市场风险。其中，指数型基金的市场风险最高，价值型和成长型基金的市场风险较为接近，而平衡型基金的市场风险相对略低。

规模因子（SMB）方面，表4中四类基金SMB的系数均为负，说明我国开放式基金偏好投资市值较大的股票。其中，指数型基金的规模因子系数绝对值最大，与我国开放式指数基金主要跟踪大盘股指数有关；与指数型基金相比，其他三类基金指数的SMB系数绝对值较小，说明其他主动型基金为了追求高于市场组合的收益，会适当增加小市值股票的投资比例。

价值因子（HML）方面，指数型基金的系数为正，说明我国指数型基金主要投资具有较高账面市值比的股票；成长型基金的HML系数为负，说明其偏向投资具有较低账面市值比的股票，与投资公告中宣称的投资风格相符；值得注意的是，价值型基金在投资公告中宣称偏重于高账面市值比的股票，但是其对应的HML系数平均为负，说明我国价值型基金依然偏好投资“成长型”股票，出现投资风格漂移现象。

注：*、**、***分别表示在10%、5%和1%的水平下显著，括号内的值为使用KRLS方法得到的t统计量。

（三）逐点的风险偏好特征

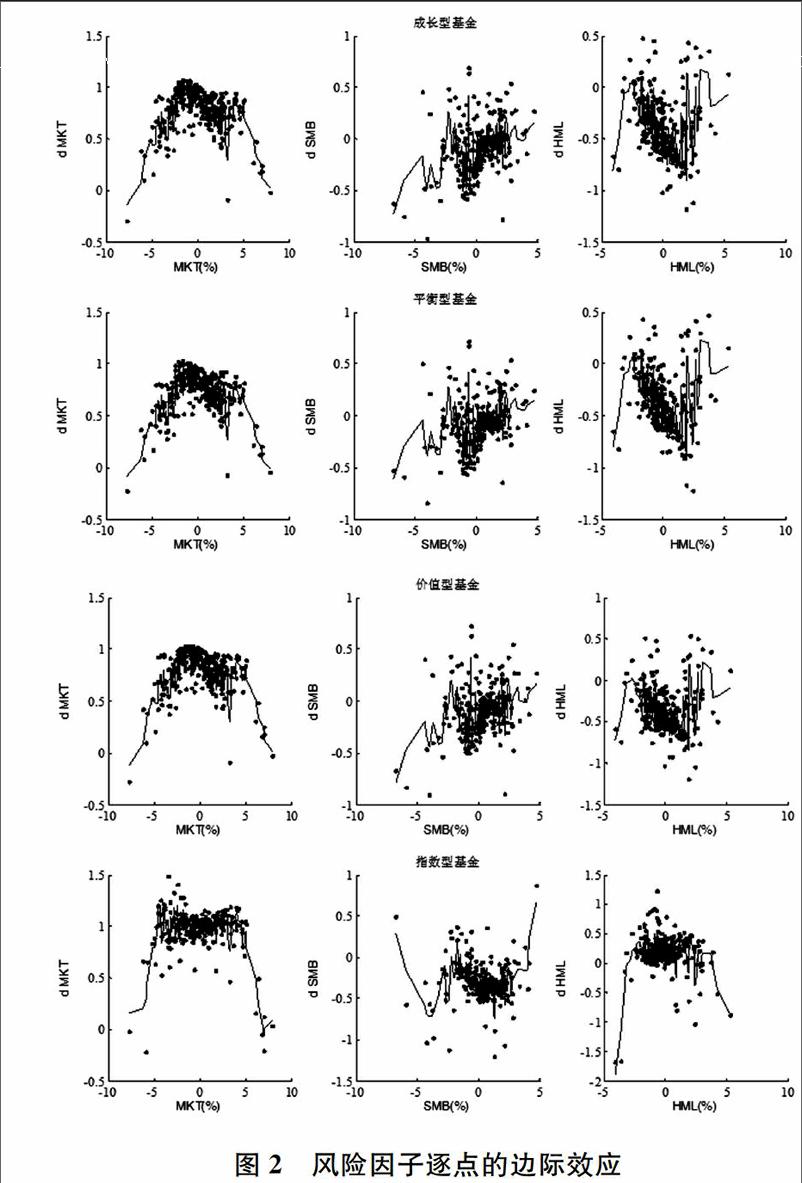
由于许多市场因素可能引起基金管理者的风险偏好发生改变，并且各风险因子与基金超额收益之间可能存在复杂的非线性关系，因此，分析各风险因子逐点的边际效应有助于全面了解基金的风险偏好特征。

图2为四种基金对应的风险因子逐点的边际效应及其變化趋势。可以看出，图2中规模因子（SMB）取值为正的情形较为多见，说明研究区间内我国股票市场存在一定的规模溢价现象。而价值因子（HML）取值为负的观测值过半，说明我国股票市场的价值效应并不明显。值得注意的是，我国成长型、平衡型和价值型基金均呈现出明显的风险调整行为，并且风险溢价的变化特征较为相似，而指数型基金的风险偏好相对稳定。除个别极端点外，指数型基金的MKT系数均接近于1，且其规模因子和价值因子系数也相对稳定。其中，我国指数型基金的SMB系数一般为负，而HML系数一般为正，说明指数型基金主要投资于“大盘股”以及具有高账面市值比的“价值型”股票。

其他三类基金指数的MKT系数均呈现先升后降的态势。说明在市场收益适中时，开放式基金倾向于持有具有较高市场风险的投资组合，而当市场组合收益较高或较低时，基金经理人会通过调整投资策略降低投资组合的市场风险。规模因子（SMB）方面，三类基金指数的SMB系数均呈现上升趋势，说明当规模溢价较低时，各类基金通常会持有较高比例的高市值股票，而随着规模溢价的增长，投资基金倾向于增加小市值股票的比例。此外，三类主动型基金的价值因子（HML）系数一般为负并且呈“V”形变化趋势，说明我国主动型基金通常偏好投资具有低账面市值比的股票，并且当HML在2%左右时成长型股票的投资比例最高。

注：图中横轴分别为市场因子（MKT）、规模因子（SMB）和价值因子（HML）的取值，纵轴为三类风险因子对应的边际效应，实线为通过局部加权回归散点平滑法（Locally Weighted Scatter Plot Smoothing，LOWESS）得到的边际效应变化趋势。

六、结论与启示

本文详细介绍了KRLS方法的模型构建和参数选择过程，并通过检验样本拟合效果和样本外预测能力证明了该方法的有效性；更重要的是，使用KRLS方法对传统定价模型进行修正，更加准确地考察了我国开放式股票型基金的风险偏好特征。研究结果表明：（1）KRLS方法的样本拟合效果和样本外预测能力均显著优于广义线性模型，这一优势在复杂非线性样本中表现更为突出。（2）从平均风险偏好来看，研究区间内我国指数型基金偏好于投资“大盘股”和“价值型”股票，而三类主动型基金偏好于投资“成长型”股票，其对“大盘股”的偏好明显弱于指数型基金。（3）我国开放式股票型基金中，指数型、成长型和平衡型基金的风险偏好基本与其投资公告中宣称的投资风格相符，但价值型基金存在明显的投资风格漂移现象。（4）我国三类主动型基金表现出明显的风险调整行为，并且风险偏好的变化特征相似，而指数型基金的风险偏好较为稳定。

本文的研究结论可以为我们带来如下启示：第一，与传统定价模型相比，核正则化最小二乘法（KRLS）更具有效性，该方法为研究金融资产风险溢价等问题提供了有效工具。第二，我国部分类型的基金与其公告的投资风格存在偏离现象，因此，投资者不应只关注基金公告的内容，而应综合考虑市场环境因素的变化，选择正确的投资策略。第三，随着风险因子的改变，我国三类主动型基金的风险偏好呈现明显变化，监管机构应当密切关注投资基金的风格演变特征。第四，我国三类主动型基金的投资偏好以及风险调整行为表现出趋同性。这不仅不利于满足投资者多元化的风险管理需求，还无益于金融市场的系统风险控制，因此，相关监管部门应当完善基金的信息披露制度，促进基金业的规范发展。

参考文献：

[1] King G，Zeng L.The dangers of extreme counterfactuals [J].Political Analysis，2006，14（2）：131-159.

[2] Brambor T，Clark W，Golder M.Understanding interaction models：improving empirical analyses [J].Political Analysis，2006，14（1）：63-82.

[3] Kim M，Shukla R，Tomas M.Mutual fund objective misclassification [J].Journal of Economics and Business，2000，52（4）：309-323.

[4] 曾晓洁，黄嵩，储国强.基金投资风格与基金分类的实证研究[J].金融研究，2004（3）：66-78.

[5] 王敬，刘阳.证券投资基金投资风格：保持还是改变？[J].金融研究，2007（8）：120-130.

[6] 艾洪德，刘聪.基金经理个人特征与基金投资风格[J].财贸经济，2008（12）：26-31.

[7] 肖继辉，彭文平.基金经理特征与投资能力、投资风格的关系[J].管理评论，2012（7）：40-48.

[8] Brown K，Harlow W，Starks L.Of tournaments and temptations：an analysis of management incentives in the mutual fund industry [J].The Journal of Finance，1996，51（1）：85-110.

[9] Taylor J.Risktaking behavior in mutual fund tournaments [J].Journal of Economic Behavior and Organization，2003，50（3）：373-383.endprint

[10] 肖继辉.基金行业锦标赛及其激励效应研究——来自开放式基金的经验证据[J].南开管理评论，2012（5）：44-55.

[11] 罗真，张宗成.职业忧虑影响基金经理投资行为的经验分析[J].世界经济，2004（4）：63-71.

[12] 刘莎莎，刘玉珍，唐涯.信息优势、风险调整与基金业绩[J].管理世界，2013（8）：67-76.

[13] 肖继辉，彭文平.锦标赛制度与基金风险调整：理论拓展与经验证据[J].管理科学学报，2015（1）：87-98.

[14] Fama E，French K.Common risk factors in the returns on stocks and bonds [J].Journal of Financial Economics，1993，33（1）：3-56.

[15] Carhart M.On persistence in mutual fund performance [J].Journal of Finance，1997，52（1）：57-82.

[16] Fama E，French K.A fivefactor asset pricing model [J].Journal of Financial Economics，2015，116（1）：1-22.

[17] Olmo J，Pouliot W.Tests to disentangle breaks in intercept from slope in linear regression models with application to management performance in the mutual fund industry [R].Department of Economics，University of Birmingham，2014.

[18] Bandi F，Renò R.Timevarying leverage effects [J].Journal of Econometrics，2012，169（1）：94-113.

[19] Rifkin R，Yeo G，Poggio T.Regularized leastsquares classification [J].Nato Science Series Sub Series III Computer and Systems Sciences，2003，190：131-154.

[20] Hainmueller J，Hazlett C.Kernel regularized least squares：reducing misspecification bias with a flexible and interpretable machine learning approach [J].Political Analysis，2014，22（2）：143-168.

[21] Tikhonov A N.Solution of incorrectly formulated problems and the regularization method [C].Soviet Math.Dokl.，1963，5：1035-1038.

[22] Hastie T，Tibshirani R，Friedman J.The elements of statistical learning：data mining，inference，and prediction [M].New York：Springer，2009.

（責任编辑：王铁军）endprint