面向HEVC的Golomb-Rice编码参数自适应策略*

夏德春,2，何小海**，韩兴阳2，叶宇昀，吴小强

(1.四川大学 电子信息学院，成都 610065；2.联合保障中心 信息中心，成都 610015)

面向HEVC的Golomb-Rice编码参数自适应策略*

夏德春1,2，何小海**1，韩兴阳2，叶宇昀1，吴小强1

(1.四川大学 电子信息学院，成都 610065；2.联合保障中心 信息中心，成都 610015)

为了进一步降低高性能视频编码(HEVC)的输出码率，针对基于上下文的自适应算术编码(CABAC)，提出了一种改进算法。利用大尺寸变换单元(TU)和变换跳过模式系数块大值系数较多的特点，首先在32×32变换单元中，根据已编码4×4系数组(CG)系数值的分布特性，自适应决定下一个CG的哥伦布-莱斯(Golomb-Rice)初始参数值；其次，在变换跳过模式系数块中设置初始Golomb-Rice参数为1，再利用相邻系数的相关性，根据已编码系数绝对值大小自适应决定下一系数的编码参数值。实验结果表明，与HEVC标准算法HM16.0相比，所提算法能达到0.09%～2.75%的比特率下降，平均有效率90%以上，且峰值信噪比(PSNR)无损失，编码时间平均只增加了0.08%。与代表文献相比，所提算法平均节省0.49%比特率，PSNR平均提高0.01 dB。

高性能视频编码；哥伦布-莱斯(Golomb-Rice)参数；变换跳过模式；自适应策略

1 引 言

为了进一步提高新一代视频编码标准-高性能视频编码(High Efficiency Video Coding，HEVC)的压缩性能，众多学者先后基于客观工程学框架和人类视觉感知模型[1-2]提出了不同改进算法，并且都达到了降低输出码率的目的。而针对熵编码的改进是其中的重要研究之一。HEVC中采取的熵编码策略是基于上下文的自适应算术编码(Context-based Adaptive Binary Arithmetic Coding，CABAC)。与其他熵编码方法相比,CABAC熵编码能够取得更好的压缩效果,特别是当信源概率分布比较均匀时,它的编码效率要高于哈夫曼编码。

近年来，针对CABAC的改进成为了众多学者研究的热点，提出了一系列改进算法[3]。文献[4]中提出了相比于CABAC更复杂的上下文树加权建模(Context-tree Weighting,CTW)方法，在计算复杂度成本显著增加的前提下，能达到约1%～3%的比特率节约。文献[5]在文献[4]的基础上，提出了一种基于CTW的概率估计模型，使编码符号的概率估计更加精确，从而能达到0.7%～4.5%的比特率节约，但解码复杂度增加了32%～38%。文献[6]将变换单元分成不同区域，同尺寸变换块的相同区域使用同一个上下文模型，并利用一个局部模板下的邻域系数确定当前上下文模型的索引值，实验结果显示在低延迟配置条件下，能达到0.9%的比特率节约。文献[7]针对屏幕内容变换跳过模式编码块系数的分布特点，对绝对系数值进行区间截断，然后进行有限长度的哥伦布-莱斯编码，能达到0.6%～1.13%的比特率节省。

但是，文献[4-5]对CABAC的改进主要集中在概率模型的精确估计上，没有直接从编码系数的分布特性来考虑。虽然有一定比特率节约，但编解码复杂度却大大增加。文献[6]虽然区分了变换块的不同区域，并利用了相邻系数的相关性，但是对系数的分布特性考虑不够，因此码率降低有限。文献[7]尽管考虑了变换跳过模式系数块系数较大的特点，却没有区分不同尺寸变换块系数幅值的差异性，故而主要对屏幕内容序列有一定效果，对普通序列效果不太明显。而且在熵编码阶段采用了有损的系数处理方式，造成了一定的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)损失。因此，本文结合编码块系数的能量分布特性，综合考虑大尺寸变换块和跳过模式编码块两个方面，对熵编码阶段的哥伦布-莱斯(Golomb-Rice)编码参数提前预测，在PSNR无损失、编解码时间几乎不增加的前提下，实现一定比特率的节约。

2 CABAC熵编码

HEVC的CABAC熵编码采用常规编码和旁路编码相结合的编码方式。常规编码模式为每个语法元素建立一个上下文模型，根据编码过程自适应更新概率值，而旁路编码模式无需为每个编码符号分配概率模型。HEVC标准算法中对常规编码后剩余绝对值部分的语法元素coeff_abs_level_remaining采取哥伦布-莱斯编码。CABAC熵编码涉及的其他语法元素参见文献[7]。

HEVC中变换单元(Transformation Unit，TU)分为4×4、8×8、16×16、32×32四种尺寸，每一个TU都被分为4×4的系数组(Coefficient Group，CG)进行熵编码。HEVC标准算法中对一个CG的熵编码过程如图1所示。

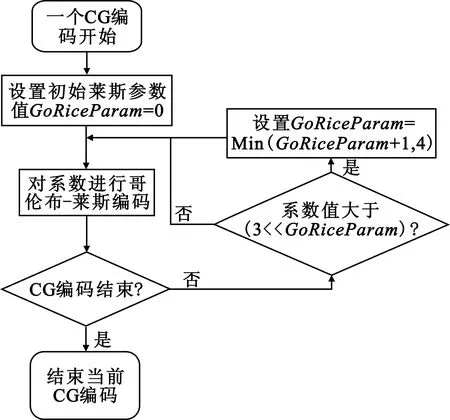
图1 一个CG的哥伦布-莱斯编码过程Fig.1 Golomb-Rice code flow chart in a CG

3 基于系数分布特性的改进算法

经过DCT变换的TU块能量主要集中于左上角，其表现为左上角的CG块大幅值系数较多,并且这种系数分布特性随着TU尺寸的增大表现得越明显。为了说明这种系数分布特性和TU尺寸的关系，我们对序列Kimono1(1 920×1 080，24 frame/s)在量化参数(Quantization Parameter，QP)为17和27时的系数绝对值分布区间进行统计，如图2。从图2可以看出，尺寸为32×32的TU块大幅值系数明显较多。另外，我们发现在一些序列中，采用变换跳过模式的编码块也具有大幅值系数较多的特征。

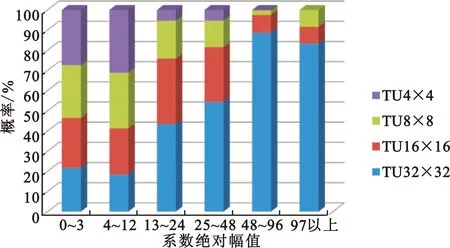
(a)QP=17

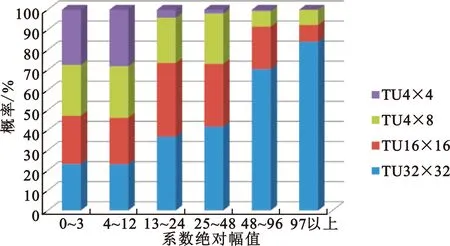
(b)QP=27图2 TU的系数绝对幅值分布特性Fig.2 The distribution of coefficient absolute amplitude in a TU

在HEVC标准算法中采用图1所示的算法对CG进行哥伦布-莱斯编码,这种算法设置初始哥伦布-莱斯参数为0，当初始编码系数绝对值较大时，编码一个系数所需的比特较多。因此，我们将尺寸为32×32的TU块和变换跳过模式编码块与其他编码块区分开来，依据编码块及系数绝对幅值之间的相关性自适应决定哥伦布-莱斯参数值，并调整参数范围为[0，6]。本算法只作用于最终熵编码阶段，不参与率失真优化等其他过程。

3.1大尺寸TU哥伦布-莱斯初始参数的决策

区分不同的TU尺寸设置不同的哥伦布-莱斯初始参数K：

(1)

式中：s为TU块的尺寸，Ki为通过阈值决策的初始莱斯参数值。Ki的具体决策过程如下式：

(2)

式中：τ1、τ2、τ3、τ4为阈值因子；Ai-1为前一CG的绝对系数幅值均值，其定义为

(3)

式中：N为编码块中非零系数的个数，xj为一个编码块中的第j个元素。

3.2变换跳过模式编码块哥伦布-莱斯参数的决策

对采用变换跳过模式的编码块设置K=1，当编码完一个coeff_abs_level_remaining后，根据当前coeff_abs_level_remaining值判断下一个编码参数Kj：

(4)

式中：Vj-1为前一个coeff_abs_level_remaining值;μ1、μ2、μ3为阈值因子；j为系数序号，且j∈[1,3]。

4 实验结果与性能分析

本文的实验平台为HEVC的标准测试软件HM16.0，共选择了6个不同分辨率的序列做测试，每个序列编码前50帧，本算法需要对变换跳过模式编码块进行处理，因此将变换跳过模式参数transformskip设置为1。为了说明算法在较大量化区间具有有效性，选择了4个QP(12、17、22、27)进行测试。其他均为HEVC推荐配置，如表1所示。全I帧编码配置文件为encoder_intra_main.cfg，帧间编码配置文件为encoder_lowdelay_P_main.cfg。

表1 编码参数配置Tab.1 Configuration of coding parameters

首先，为了说明算法的有效性，特定义有效率η如下：

(5)

式中：∑Feff代表编码比特率有下降的帧数之和;∑Ftotal代表总帧数;η表示相比于HM16.0比特率有下降的帧数占总帧数的比值,比值越大，说明提出的方法越有效。有效率统计如表2,从表中我们可以看出，η的平均值在90%以上，充分说明了本文算法的有效性。

表2 相比于HM16.0本文算法有效率统计Tab.2 Efficiency of the algorithm compared with HM16.0 %

其次，实验在码率、峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和编码时间3个方面将本文算法与HEVC标准测试算法HM16.0的性能进行比较。ΔB、ΔP、ΔT分别表示本文算法与HM16.0标准的码率差值百分比、PSNR差值、编码时间差值百分比，则

(6)

ΔP=Pproposed-PHM16.0,

(7)

(8)

式中：Bproposed、Pproposed、Tproposed分别表示本文算法的编码码率、PSNR和编码时间，BHM16.0、PHM16.0、THM16.0分别表示HM16.0标准的编码码率、PSNR和编码时间。实验结果显示，ΔP均为0，其余指标如表3和表4所示。

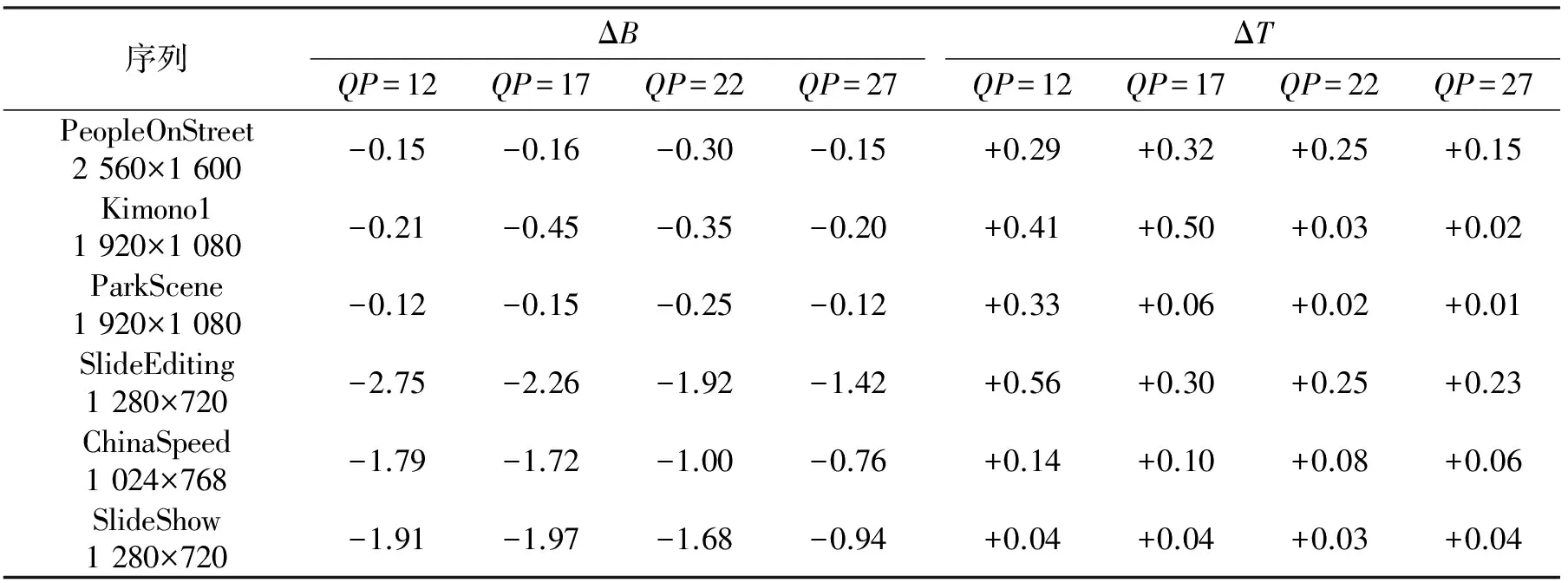
表3 全I帧编码性能比较Tab.3 Comparison of intra frame coding performance %

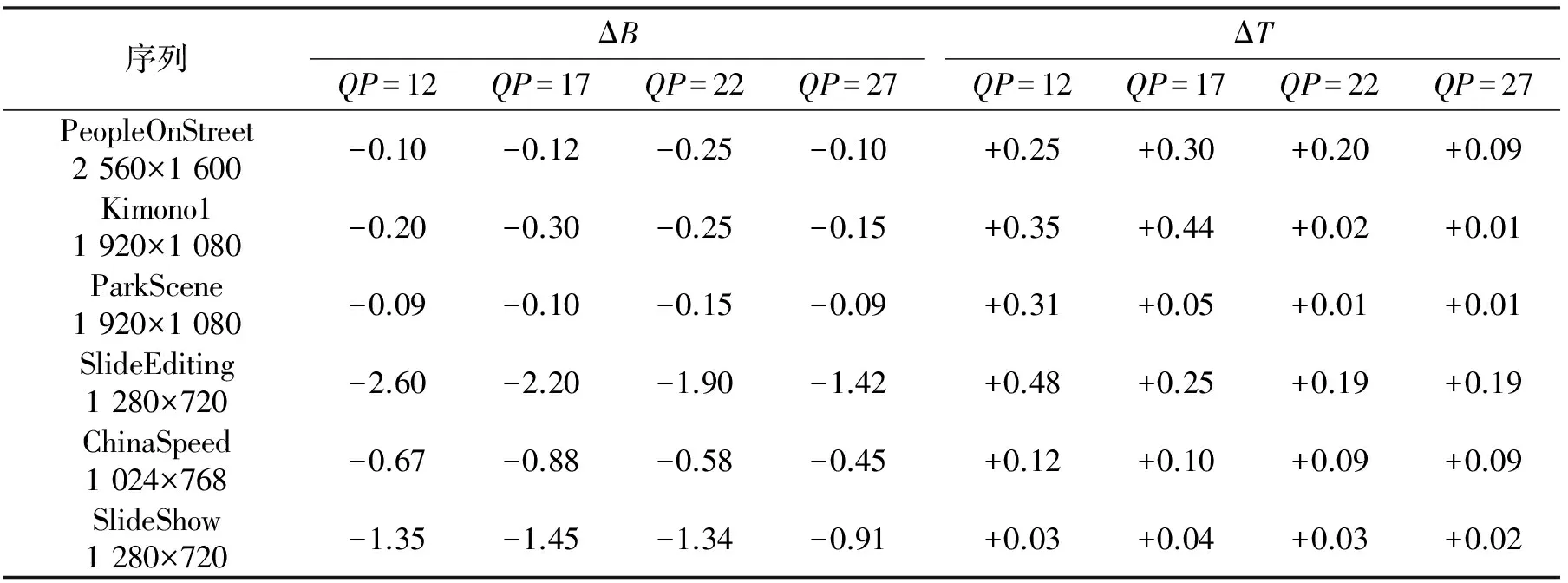
表4 帧间编码性能比较Tab.4 Comparison of inter frame coding performance %

从表3和表4可以看出，本文所提算法与HEVC标准测试算法HM16.0相比，比特率有一定下降，且帧内效果优于帧间。这是由于帧内编码系数绝对幅值比帧间更大。其次，所提算法只作用于最终熵编码阶段，通过解码序列与重构序列的比较，PSNR完全没有损失。另外，本算法不额外增加迭代等复杂运算，因此编码时间增加不大。

图3给出了PeopleOnStreet(2 560×1 600，30 frame/s)、Kimono1(1 920×1 080，24 frame/s)、SlideEditing(1 280×720，30 frame/s)和ChinaSpeed(1 024×768，30 frame/s)4个序列的率失真曲线。从图中曲线可以看出,本文所提算法率失真性能优于HM16.0。

(a)PepoleOnstreet

(b)Kimomol

(c)SlideEditing

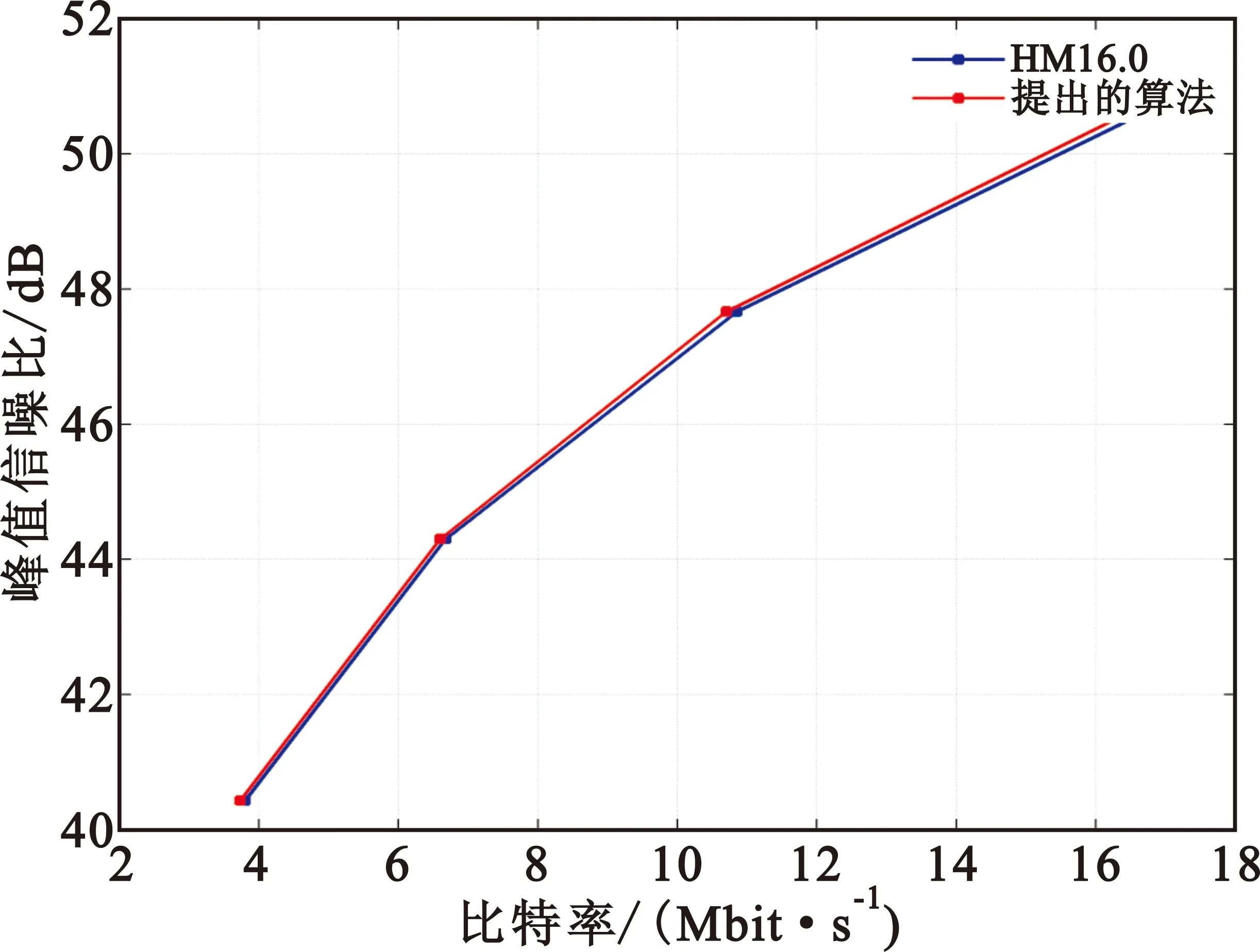
(d)ChinaOnspeed

为了进一步验证本文算法的良好性能，本文算法在与文献[7]算法相同配置条件下进行实现，表5给出了本文算法在全I帧配置下对比文献[7]算法的率失真结果。表中ΔB、ΔP为两种算法与标准测试软件码率差值百分比、PSNR差值。从表5的数据可以看出，在相同的配置条件下，本文算法相比文献[7]的算法能节约0.49%比特率。这是因为本文算法能够根据系数的分布特性提前预测编码参数值,减少了输出比特。其次,本文算法没有PSNR的损失，而文献[7]的算法PSNR平均损失0.01 dB。这是因为文献[7]的算法对系数进行截断，本身就对系数造成一定损失，而本文算法只作用于最后熵编码阶段，只是根据编码块及系数绝对幅值之间的相关性预测编码参数值，对PSNR无影响。

表5 本文算法文献[7]算法的率失真性能比较Tab.5 Comparison of the rate distortion performance between the propsed algorithm and the algorithm in Referen[7]

图4给出了序列SlideEditing(1 280×720，30 frame/s)的率失真曲线，可以明显看出本文算法优于文献[7]的算法。

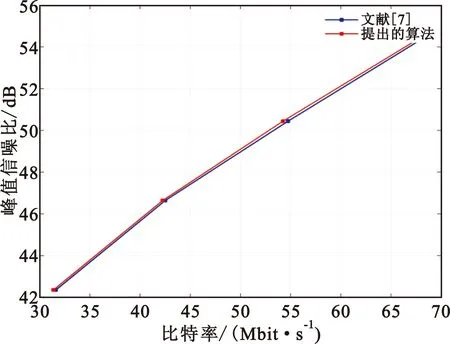
图4 SlideEditing的率失真曲线Fig.4 Rate distortion curve of SlideEditing

5 结束语

本文通过对编码系数分布特性的分析，得出了大尺寸TU和采用变换跳过模式编码块大幅值系数较多的结论。在尺寸为32×32的TU块中，根据已编码CG的系数自适应决定下一CG的初始哥伦布-莱斯参数值；在采用变换跳过模式的系数块中，设置初始哥伦布-莱斯参数为1，再根据已编码系数绝对值大小自适应决定下一系数的编码参数值。实验结果表明，本文算法相比于HM16.0标准算法，在PSNR无损失的情况下，达到了0.09%～2.75%的比特率下降。与代表文献相比，本文算法能平均节省0.49%比特率，PSNR平均提高0.01 dB。从实验数据可以看出，本文算法能一定程度降低输出码率，且对不同分辨率视频及较大QP区间都具有较好效果。随着4K和8K等高清视频逐渐成为主流视频，TU尺寸的增大成为了必然趋势[8]，因此本文算法将具有更广阔的应用前景。下一步将考虑怎样将本文算法应用到更大尺寸TU之中。

[1] 林国川,何小海,李向群,等.基于感兴趣区域的HEVC压缩性能优化[J].电讯技术,2016,56(1):38-43.

LIN Guochuan,HE Xiaohai,LI Xiangqun,et al.ROI-based HEVC video compression optimization[J].Telecommunication Engineering,2016,16(1):38-43.(in Chinese)

[2] 王晓龙.基于感兴趣区域的自适应帧内更新编码算法[J].电讯技术,2014,54(5):569-573.

WANG Xiaolong. Adaptive intra update coding algorithm based on region of interest video coding[J].Telecommunication Engineering,2014,54(5):569-573.(in Chinese)

[3] ZHANG H,SONG L,YANG X K,et al.Evaluation of beyond-HEVC entropy coding methods for DCT transform coefficients[C]. //Proceedings of 2016 Visual Communication and Image Processing(VCIP). Chengdu:IEEE,2016:1-4.

[4] HONG D,VANSCHAAR M D,PESQUETPOPESCU B. Arithmetic coding with adaptive context-tree weighting for the H.264 video coders[C]. // Proceedings of SPIE The International Society for Optical Engineering. San Jose,CA：SPIE,2004:1226-1235.

[5] KARWOWSKI D,DOMASKI M. Context-adaptive binary arithmetic coding with precise probability estimation and complexity scalability for high-efficiency video coding[J].Journal of Electronic Imaging,2016,25(1)：1-16.

[6] GAO M,FAN X P,ZHAO D B,et al.An enhanced entropy coding scheme for HEVC[J].Signal Processing:Image Communication,2016,44:108-123.

[7] CHOI J A,HO Y S. Improved entropy coding for quantized transform coefficients in HEVC screen content coding[J].Signal,Image and Video Processing,2015,9(5):1067-1079.

[8] ALSHIN A,ALSHINA E,BUDAGAVI M,et al.Coding efficiency improvements beyond HEVC with known tools[C]//Proceedings of SPIE9599(Applications of Digital Image Processing XXXVIII).San Diego,California:SPIE,2015:1-14.

HEVC-orientedGolomb-RiceParameterAdaptiveStrategy

XIA Dechun1,2,HE Xiaohai1,HAN Xingyang2,YE Yuyun1,WU Xiaoqiang1
(1.College of Electronics and Information,Sichuan University,Chengdu 610065,China;2.Information Center,Joint Support Center,Chengdu 610015,China)

In order to further reduce high efficiency video coding(HEVC) output rate,this paper presents an improved algorithm of Context-based Adaptive Arithmetic Coding(CABAC). Firstly,by using the feature that the large size transform unit(TU) and the transform skip mode coefficient block has more large coefficients in CABAC,according to the distribution characteristics of the coded 4×4 coefficients array(CG) in 32×32 transform unit,the initial Golomb-Rice parameter of the next CG is adaptively determined.Then,in the transform skip mode coefficient block,the initial Golomb-Rice parameter is set to 1,and then the coding parameter of the next coefficient is adaptively determined according to the absolute value of the coded coefficients. The experimental results show that,compared with the HEVC standard algorithm HM16.0,the proposed algorithm brings down the bit rate by 0.09%～2.75%,the average efficiency is more than 90%,peak signal-to-noise ratio(PSNR) has no loss and coding time is only increased by 0.08%. Compared with the representative literature,the proposed algorithm can save the average bit rate by 0.49%,and PSNR is increased by an average of 0.01 dB.

high efficiency video coding(HEVC)；Golomb-Rice parameter；transform skip mode;adaptive strategy

date:2017-01-06；Revised date：2017-04-10

国家自然科学基金资助项目(61471248);四川省科技计划项目(2015JY0189);四川省教育厅2014年研究生教育改革项目(2014-教-034)

**通信作者：hxh@scu.edu.cn Corresponding author：hxh@scu.edu.cn

TN919.81

A

1001-893X(2017)10-1218-06

夏德春(1984—)，男，四川广元人，2008年于四川大学获学士学位，现为硕士研究生，主要研究方向为图像与视频编码；

Email:xiazhi2003169@163.com

何小海(1964—)，男，四川绵阳人，2002年于四川大学获博士学位，现为教授，主要研究方向为图像处理、模式识别和图像通信；

Email:hxh@scu.edu.cn

韩兴阳(1979—)，男，四川广元人，2009年于国防大学获硕士学位，现为助理工程师，主要研究方向网络安全与信息建设、图像处理；

叶宇昀(1993—)，男，福建漳州人,2015年于东北大学获学士学位，现四川大学硕士研究生，主要研究方向为视频压缩和图像通信；

吴小强(1969—)，男，广西柳州人，1991年于成都科技大学获学士学位，现为高级工程师，主要研究方向为图像处理、图像通信及计算机应用。

10.3969/j.issn.1001-893x.2017.10.019

夏德春，何小海，韩兴阳,等.面向HEVC的Golomb-Rice编码参数自适应策略[J].电讯技术，2017,57(10):1218-1223.[XIA Dechun,HE Xiaohai,HAN Xingyang,et al.HEVC-oriented Golomb-Rice parameter adaptive strategy[J].Telecommunication Engineering,2017,57(10):1218-1223.]

2017-01-06；

2017-04-10