基于t检验的星基增强系统完好性数据核验*

王 娇**，2，陈 潇，邓平科，吴海涛

(1. 中国科学院 光电研究院，北京 100094；2.中国科学院大学，北京100049)

基于t检验的星基增强系统完好性数据核验*

王 娇**1，2，陈 潇1，邓平科1，吴海涛1

(1. 中国科学院 光电研究院，北京 100094；2.中国科学院大学，北京100049)

针对星基增强系统(SBAS)高完好性的服务需求，提出了一种SBAS广播参数用户差分伪距误差(UDRE)的完好性核验方法。利用监测站实测全球定位系统(GPS)和地球静止轨道(GEO)卫星信号，解析GPS电文和SBAS广播差分及完好性信息，对观测量修正误差得到实测UDRE，使用t检验成对二样本分析法验证给定置信区间内广播UDRE′与实测UDRE的符合性，从而完成伪距域完好性参数UDRE的核验。伪距域的核验避免了以往位置域核验计算量大、多卫星故障检测能力差的缺点，有更好的故障检测与隔离能力。采集日本多功能GPS卫星星基增强系统(MSAS)数据并对提出的t检验方法进行验证，结果表明，所建立的统计检测量能有效地反应被监测卫星广播UDRE参数的完好性，通过确定卫星99.9%置信度下的判决门限，对广播UDRE与实测UDRE判别，验证伪距误差的可信度。该结果验证了所提方法应用于UDRE核验的可行性，为SBAS完好性验证提供了技术支撑。

星基增强系统(SBAS);用户差分伪距误差(UDRE);完好性核验；t检验成对二样本分析法

1 引 言

星基增强系统(Satellite-based Augmentation System,SBAS)通过地球静止轨道(Geostationary Earth Orbit,GEO)卫星将差分校正信息和完好性信息发给用户来满足高精度高安全性用户的需求。GEO播发的差分改正数包括卫星星历改正、卫星钟差改正和电离层格网点垂直延迟改正。完好性是指导航系统发生任何故障或者误差超限，而无法用于导航等服务时，系统向用户及时发出报警的能力。

完好性参数包括用户差分伪距误差(User Differential Range Error,UDRE)和电离层格网点垂直改正误差(Grid Ionospheric Vertical Error,GIVE)[1]。UDRE是与卫星星历及钟差改正相应的误差，与系统本身有直接关系，更新周期6 s。GIVE是与电离层延迟相应的误差，受外界大气因素影响，更新周期120 s。从用户安全的角度考虑，完好性有着比精度更加重要的地位。从更新周期来看，UDRE对定位误差的影响更灵敏，所以对于SBAS的完好性核验主要针对UDRE进行。

目前,SBAS用户的完好性判定是通过计算用户端位置域完好性阈值与告警限值相比较来实现的[2]。位置域的核验主要针对用户端，给出所有卫星的综合定位误差。国外从事SBAS研究的学术组织开展了大量完好性分析的研究工作[3-7]。文献[4]提出天线群延迟对阈值计算的影响并给出改进算法，但位置域方法存在计算量大、多卫星故障检测能力差的缺点。本文针对卫星端核验完好性，基于t检验成对二样本分析法，核验单颗卫星伪距域UDRE参数，能更直接地检测由多颗卫星故障造成的误差超限。

根据完好性的定义，UDRE可定义为系统服务区内，卫星星历及钟差改正数误差相对应伪距误差的置信限值(置信度为99.9 %)[1]。UDRE的伪距域核验是在给定置信度下，核验广播UDRE是否良好反应卫星星历及钟差改正数误差相对映伪距误差。

2 UDRE核验方法

通过对监测站实测UDRE与卫星广播UDRE′进行假设检验，验证SBAS系统伪距域的完好性性能，基本流程图如图1所示。

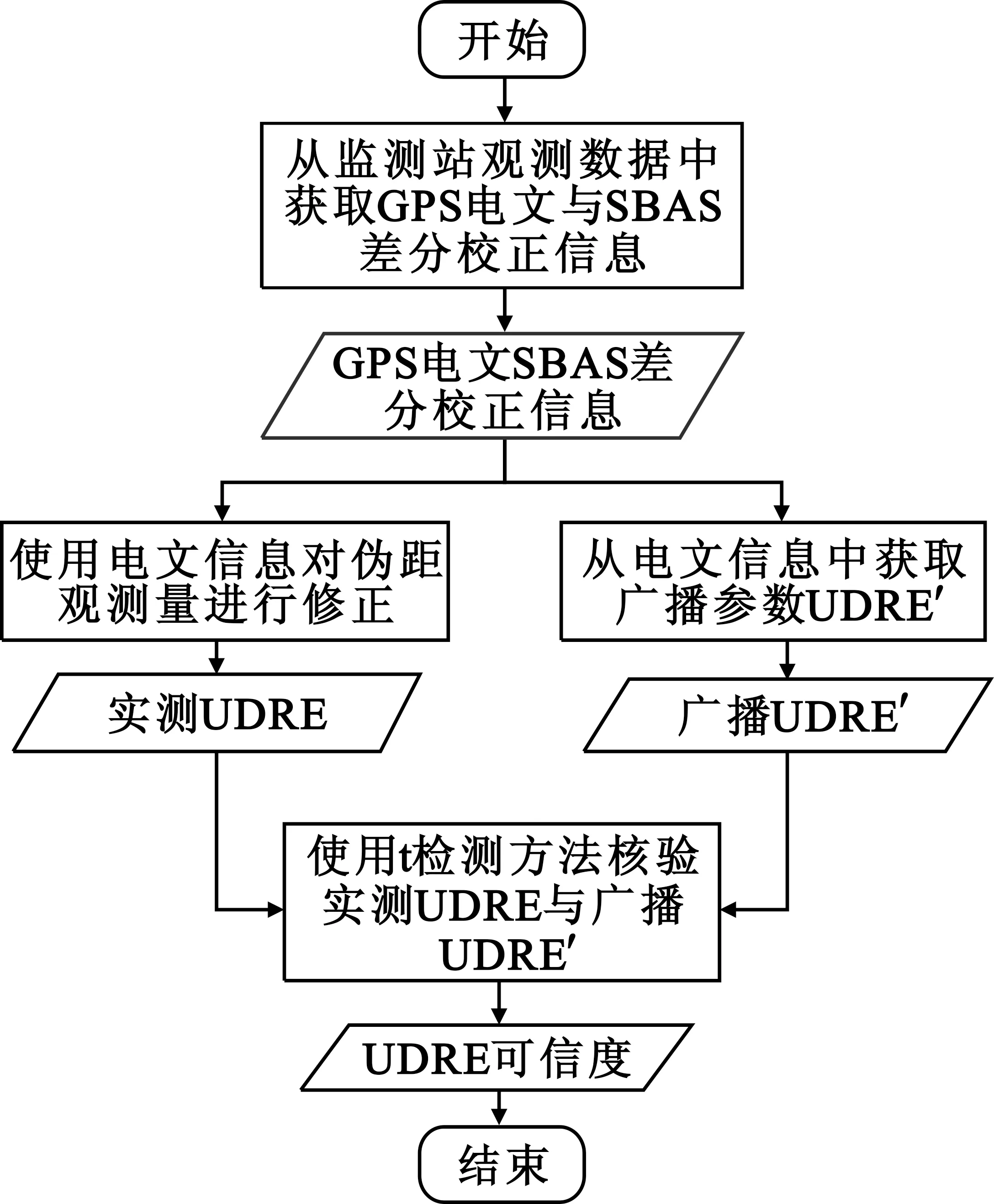
图1 伪距域核验流程图Fig.1 Flow chart of checking in range domain

通过监测站观测数据获取全球定位系统(Global Positioning System,GPS)电文与SBAS差分校正信息，经伪距误差修正后得到实测UDRE，同时，解析SBAS广播UDRE′参数，使用t检验成对二样本分析法，对相同条件下的成对观察值进行比较分析，验证99.9%置信区间内广播UDRE′与实测UDRE的符合性，得到伪距误差的可信度。

2.1伪距误差修正

GPS伪距误差修正包括GPS误差修正和SBAS差分修正。文献[8]详细阐述了GPS误差修正方法，包括卫星时钟误差修正、卫星星历误差修正、相对论效应修正、电离层延迟修正以及对流层延迟修正，公式如下：

ρ=r-δt(s)+δtu-R+I+T+ερ。

(1)

式中：ρ为伪距观测量，r为卫星与用户的几何距离，δt(s)为广播星历引起的伪距修正值，δtu为监测站接收机钟差引起的伪距修正值，R为相对论效应引起的伪距修正值，I为电离层误差修正值，T为对流层误差修正值，ερ为经过GPS误差修正后的残差。

对经过GPS误差修正的伪距观测量再进行SBAS误差修正，即可得到图2中修正后的伪距ρ′。ρ′与真距做差后得到伪距误差UDRE如下：

ερ=Δr-δtL-δtF+ΔUDRE+ΔGIVE。

(2)

式中：δtL和δtF为SBAS慢钟修正值和快钟修正值，Δr为SBAS位置修正值，ΔUDRE为用户差分伪距误差，ΔGIVE为电离层格网点垂直改正误差。误差修正过程中采用双频观测量消除电离层延时误差，近似于实际电离层误差，所以公式(2)得到的ΔUDRE为修正各项误差后的残差。伪距误差修正流程图如图2所示。

图2 伪距误差修正Fig.2 Flow chart of error correction of pseudorange

根据文献[1]规定的SBAS播发电文的格式及对应的差分校正值，见表1。

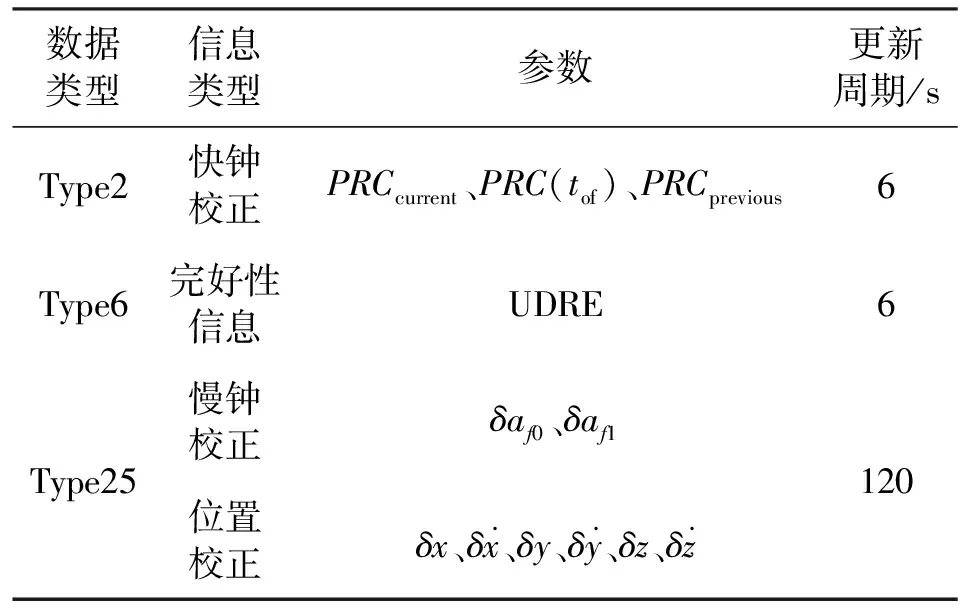
表1 SBAS数据格式Tab.1 Data format of SBAS message

卫星的SBAS快钟修正值由以下公式计算：

ρcorrected(t)=ρmeasured(t)+PRC(tof)+

RRC(tof)×(t-tof) 。

(3)

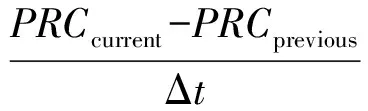
卫星的SBAS慢钟修正值由以下公式计算：

δtL=δaf0+δaf1(t-t0) 。

(4)

式中：δaf0、δaf1为慢钟校正值,t为当前时刻。

卫星的SBAS位置修正值由以下公式计算：

(5)

(6)

(7)

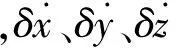
用户差分伪距误差UDRE包含了卫星轨道及钟差改正残差，以及对流层残差、接收机噪声等。由修正后的伪距ρ′与真距d做差得出

ΔUDRE=ρ′-d。

(8)

真距d是由监测站已知坐标和经过改正的卫星坐标计算得到，这里的改正是对广播星历外推的卫星发射时刻位置进行星历改正和SBAS位置改正。

修正后的伪距ρ′是由伪距观测值经卫星钟差改正、电离层改正、对流层改正、接收机钟差改正以及增强系统快钟、慢钟改正而得到的修正后的伪距。

2.2t检验成对二样本分析法

在假设检验中，t检验适用于比较相同条件下成对观察值的差异，SBAS广播UDRE′与误差修正后的实测UDRE符合此特征，本文中使用t检验对相同条件下得到的UDRE与UDRE′观察值进行比较来核验完好性。

H0:μD≥0(即认为广播UDRE′的值要比实测UDRE的值高，即真实误差在卫星广播误差估计值限值内，卫星播发的校正参数可信)；

H1:μD<0(即认为广播UDRE′的值要比实测UDRE的值低)。

(9)

当假设H0成立时，T服从自由度为n-1的t分布。对给定α=0.001(对应UDRE定义中99.9%置信度[1])，由t分布表即可得检测临界值-tα(n-1)，使

P{T≤-tα(n-1)}=α。

(10)

若T≤-tα(n-1)，拒绝假设H0；若T>-tα(n-1)，则接受假设H0。

3 实验结果及分析

实验使用NovAtel多频GNSS接收机，实验地点在北京地区。接收机可接收的卫星信号有GPS、“北斗”、GLONASS(Global Navigation Satellite System)以及MSAS (Multifunctional Satellite Augmentation System)、GAGAN(GPS Aided GEO Augmented Navigation)。MSAS和GAGAN都是对GPS进行增强的SBAS系统，验证过程采用任一系统即可。本实验对MSAS的数据进行核验分析。

为了得到相互独立的数据，对接收机数据进行间隔100 s的采样，分析GPS电文与MSAS电文并进行伪距修正，可得到两组相互独立的观察值：广播UDRE′与实测UDRE。

图3为卫星编号6的GPS卫星的实测数据结果，图 4为卫星编号5的GPS卫星的实测数据结果，红色线为MSAS卫星广播的误差估计限值，绿色线为经过差分校正后的实测误差。

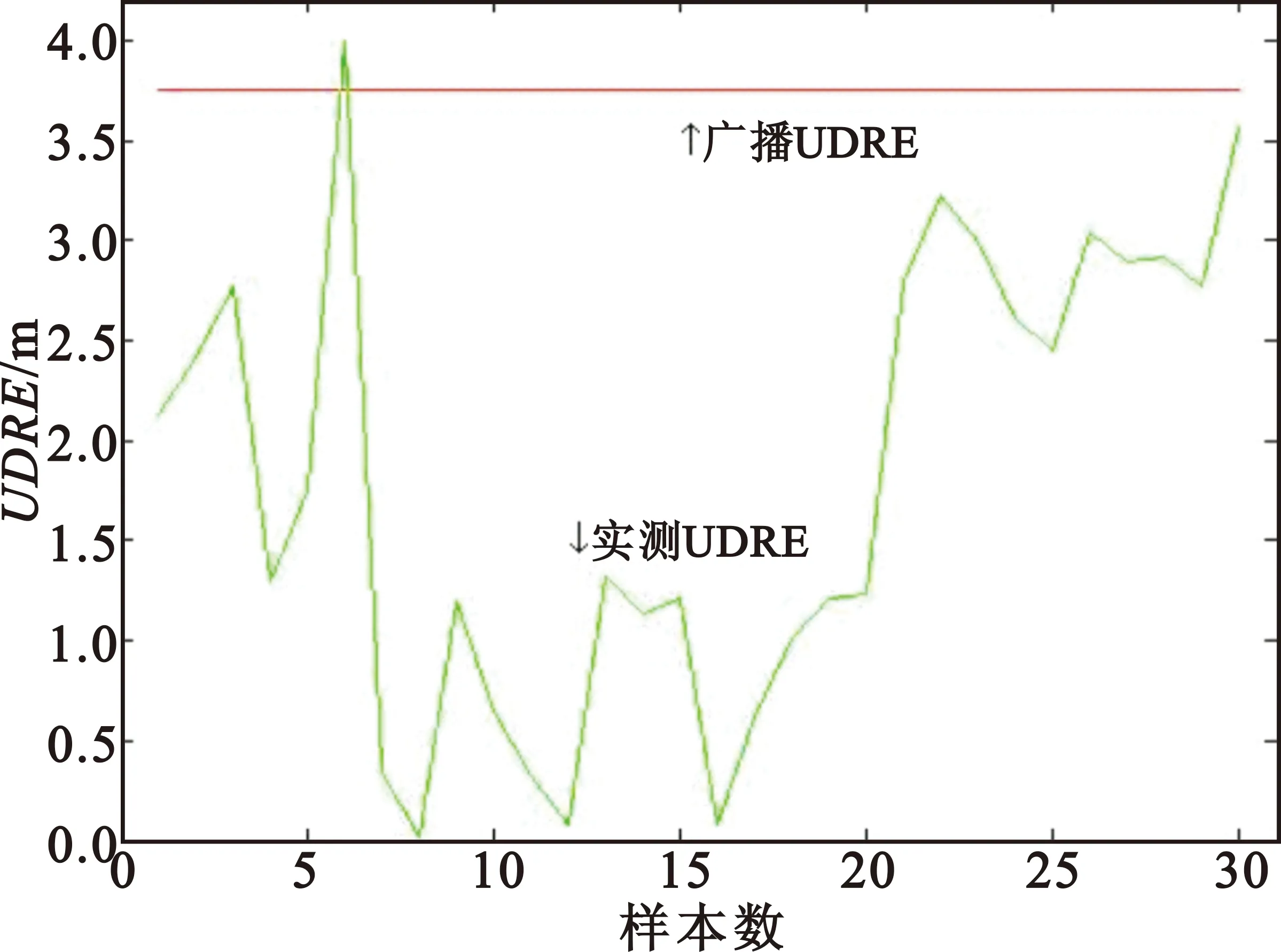
图4 卫星编号5的GPS卫星Fig.4 GPS satellite when PRN=5

对于图 3的样本，是针对卫星编号6的GPS卫星进行检验，检测统计量为15.584 59，大于临界值-3.231 71，接受H0假设，即置信度为99.9%的情况下，卫星播发的校正参数可信。从图 3中也可以直观地看到，真实误差在广播误差估计值的限值内。

对于图 4的样本，是针对卫星编号5的GPS卫星进行检验，检测统计量为9.562 64，大于临界值-3.385 18，同样接受H0假设。

为了验证卫星故障时算法的可用性，而实际中难采集到故障样本，使用Matlab模拟卫星故障并且广播UDRE′没有反映此故障。仿真采用真实卫星数据，选取其中的伪距观测量进行误差加入，而广播UDRE′仍采用真实数据，由此造成实测UDRE大于广播UDRE′，得到样本图如图5。对于图5的仿真样本，检测统计量为-8.913 20，小于临界值-3.231 71，拒绝H0假设，即置信度为99.9%的情况下，卫星播发的校正参数不可信。

图5 故障卫星仿真Fig.5 Simulation of fault satellite

实验结果表明，t检验成对二样本分析法在只分析单颗卫星数据的条件下能实现完好性检验，探测卫星故障。

4 结 论

基于t检验的伪距域完好性核验，对所有可见星逐颗进行UDRE核验，可直接检测故障卫星。对MSAS采集数据的结果表明，该方法可验证给定置信度下广播UDRE′与实测UDRE的符合性，从而判定卫星完好性，相比与位置域的完好性核验，对多故障情况有快速的检测能力，为SBAS完好性监测提供了技术参考。进一步工作可针对我国“北斗”的星基增强系统进行核验，提出技术建议。

[1] RTCA. Minimum operational performance standards for global positioning system/wide area augmentation system airborne equipment:RTCA DO-229D[S]. Washington D C:RTCA Special Committee(SC)-159,2006.

[2] OBER P B,IMPARATO D,VERHAGEN S,et al.Empirical integrity verification of GNSS and SBAS based on the extreme value theory[J].Navigation-Journal of The Institute of Navigation,2014,61(1):23-38.

[3] OBER P B. Galileo and EGNOS integrity validation:NSO-GIMAT-INT-TN-R-001[R],GIMAT Internal Document,2011.

[4] RAGHUVANSHI A,GRAAS F. Impact of antenna group delay variations on protection levels[C]//Proceedings of 2016 IEEE Position Location and Navigation Symposium(PLANS).Savannah,GA,USA:IEEE,2016. 857-862.

[5] PANAGIOTAKOPOULOS D,MAJUMDAR A. Extreme value theory-based integrity monitoring of global navigation satellite systems[J].GPS Solutions,2014,18(1):133-145.

[6] KANNEMANS H. The generalized extreme value statistical method to determine the GNSS integrity performance,Technical Report:NLR-TP-2010-491[R]. 2010.

[7] VEERMAN H,VAN KLEEF A,WOKKE F. A tool for GNSS integrity verification based on statistical extreme value theory[C]//Proceedings of 2012 Institute of Navigation′s International Technical Meeting(ION ITM).Newport Beach,CA:ION,2012:1655-1665.

[8] 谢钢. GPS原理与接收机设计[M].北京:电子工业出版社,2009.

[9] SCHEMPP T R,TIMOTHY R,RUBIN A L,et al.An application of Gaussian overbounding for the WAAS fault free error analysis[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation(ION GPS 2002). Portland,OR:ION,2002:766-772.

Satellite-basedAugmentationSystem(SBAS)IntegrityMonitoringBasedont-testMethod

WANG Jiao1,2,CHEN Xiao1,DENG Pingke1,WU Haitao1
(1.Academy of Opto-Electronics,Chinese Academy of Sciences，Beijing 100094,China；2.University of Chinese Academy of Sciences，Beijing 100049,China)

According to the integrity requirement of the satellite-based augmentation system(SBAS),a method is presented for checking user differential range error(UDRE) broadcasted by SBAS. After the range measurement is processed by using global positioning system(GPS) ephemeris and SBAS differential message reference station,true UDRE is obtained and broadcast UDRE′ is checked in range domain with t-test method. The shortcomings of position domain checking such as enormous computation power and limited statistical fault detection capability are avoided by range domain checking. Results of collecting Japan′s Multifunctional Satellite Augmentation System(MSAS) data to verify the proposed method show the established statistical detection can effectively indicate the availability of the monitoring satellite under a threshold of 99.9% availability.Through comparing the broadcast UDRE with the true UDRE,the credibility of the pseudorange errors is proved. The method is feasible for UDRE monitoring and provides a reference for SBAS integrity verification.

satellite-based augmentation system(SBAS);integrity verification；user differential range error(UDRE);t-test method

date:2017-02-27；Revised date：2017-05-10

**通信作者：wangjiao14@mails.ucas.ac.cn Corresponding author：wangjiao14@mails.ucas.ac.cn

TN967.1

A

1001-893X(2017)10-1213-05

王娇(1992—)，女，黑龙江宝清人，硕士研究生，主要研究方向为导航及其完好性理论；

Email:wangjiao14@mails.ucas.ac.cn

陈潇(1983—)，男，陕西人，高级工程师，主要研究方向为导航系统仿真；

邓平科(1977—)，男，甘肃人，副研究员，主要研究方向为卫星导航技术；

吴海涛(1966—)，男，安徽人，研究员，主要研究方向为时间同步技术、导航增强技术。

10.3969/j.issn.1001-893x.2017.10.018

王娇，陈潇，邓平科,等.基于t检验的星基增强系统完好性数据核验[J].电讯技术，2017,57(10):1213-1217.[WANG Jiao,CHEN Xiao,DENG Pingke,et al.Satellite-based augmentation system(SBAS) integrity monitoring based on t-test method[J].Telecommunication Engineering,2017,57(10):1213-1217.]

2017-02-27；

2017-05-10