滚筒飞剪传动设计参数计算方法
吴永杰,严 升,孙亚波,崔卫华
(1.中国重型机械研究院股份公司,陕西 西安 710032;2.广西柳州钢铁集团有限公司,广西 柳州 545000)
滚筒飞剪传动设计参数计算方法
吴永杰1,严 升2,孙亚波1,崔卫华1
(1.中国重型机械研究院股份公司,陕西 西安 710032;2.广西柳州钢铁集团有限公司,广西 柳州 545000)
在滚筒飞剪原有传动参数计算方法基础上,考虑连续工作制,研究了用户要求的最小目标定尺长度对传动设计参数的影响。根据滚筒飞剪连续定尺剪切原理,建立目标定尺长度计算模型,形成了比较完善的基于最小目标定尺长度的滚筒飞剪传动设计参数计算方法。以某汽车板重卷检查机组的滚筒式飞剪机为例,进行了仿真计算。结果表明,考虑最小目标定尺长度时,滚筒飞剪的传动功率增大,传动速比减小。
滚筒飞剪;连续工作制;最小目标定尺长度;传动设计参数
0 前言
经冷轧机组轧制后的带钢,必须经过精整处理加工,才能得到高质量的合格产品。精整机组主要进行重卷、纵切、横切、表面检查等工序。
现代化冷连轧机组不断向高速、自动化方向发展,且运行速度越来越高,对精整设备提出运行速度更快、精度更高、质量更好的要求。飞剪作为横切机组的重要设备对于机组的速度、精度和质量都起着关键的作用,滚筒飞剪正是在这种形势下研制开发的。之所以称为滚筒飞剪,是因为飞剪的剪刃安装在滚筒状剪轴螺旋形的槽中,随着剪轴的转动两个剪刃像齿轮啮合一样将带材剪断。
滚筒飞剪的传动设计参数包含传动功率、速比。其常规计算方法[1~12]按照启停工作制计算传动功率、速比。没有考虑连续工作制时,用户要求的最小目标定尺长度对传动设计参数的影响,从而造成最小目标定尺长度剪切无法实现。
本文深入研究了滚筒飞剪连续定尺剪切原理,建立了目标定尺长度计算模型,形成比较完善的基于最小目标定尺长度的滚筒飞剪传动设计参数计算方法。
1 原有传动参数计算方法
如图1所示,双剪刃滚筒飞剪在滚筒上对称安装了两把剪刃,沿滚筒轴线呈螺旋状布置,螺旋升角为3°,滚筒旋转一周,剪切两次,剪刃零位为两剪刃位于水平位置。
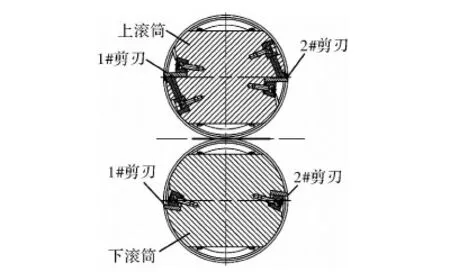
图1 飞剪滚筒结构图
如图2所示,剪切时,剪刃从零位开始旋转,转过角度α0接触带材表面,继续转过角度γ,完全剪断带材。则α0为上、下剪刃接触带材表面的加速角,γ为切入角,Δ为上下剪刃重叠量,mm。
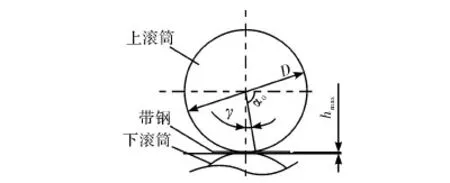
图2 飞剪剪切示意图
切入角γ计算如下
(1)
式中,D为滚筒直径,mm;hmax为钢最大厚度,mm。
加速角α0为
α0=90°-γ
式中,α0为剪切带材宽度等于剪刃长度时的加速角,考虑最宽带材比剪刃长度小,剪切最宽带材时,剪刃接触带材的加速角α变为
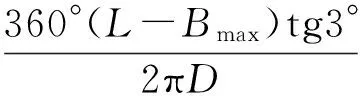
(2)
式中,Bmax为带钢最大宽度,mm。
按照最大剪切速度核算加速时间Ta为
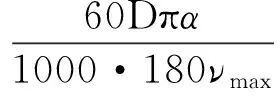
式中,νmax为最大剪切速度,m/min。
加速力矩Ma为
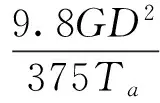
式中,GD2为飞剪换算到电机轴上的飞轮矩,kg·m2;N为传动电机额定转速,r/min。
则飞剪加速功率Pa为
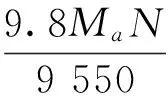
剪切最宽带材时,剪切角β为
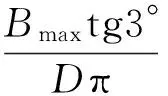
剪切制动角φ为
φ=180°-α-β
按照最大剪切速度核算制动时间Td为
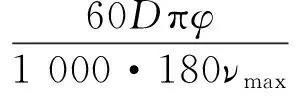
制动力矩Md为
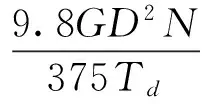
式中,GD2为滚筒换算到电机轴上的飞轮矩,kg·m2;N为传动电机额定转速,r/min。
制动功率Pd
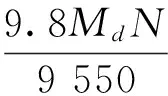
飞剪传动功率P取加速功率Pa与制动功率Pd较大者,即
P=max{Pa,Pd}
(3)
飞剪传动速比为
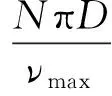
(4)
原有计算方法按照启停工作制计算,没有考虑连续工作制时,用户要求的最小目标定尺长度对传动设计参数的影响,从而造成最小目标定尺长度剪切无法实现。
2 连续定尺剪切计算分析
2.1 基本定尺长度计算
带材定尺剪切需要剪切两刀,第一刀剪切完成后,滚筒保持剪切速度运行,旋转180°后,进行第二刀剪切,则,基本定尺长度为
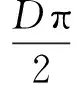
当目标定尺长度Ls>L0时,第一刀剪切后,滚筒必须先降速,保持匀速,再升速到剪切速度,进行第二刀剪切。
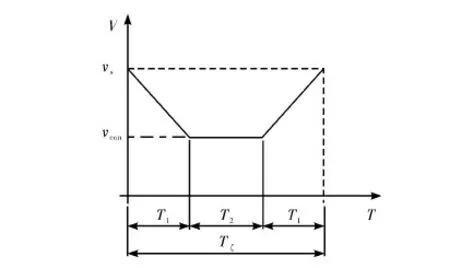
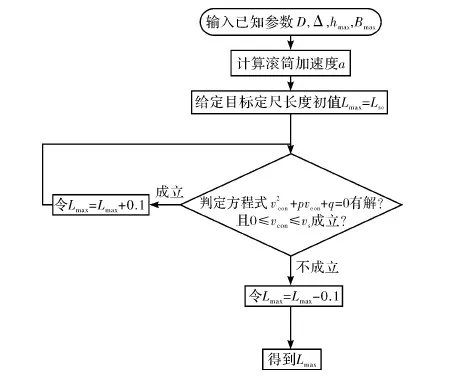
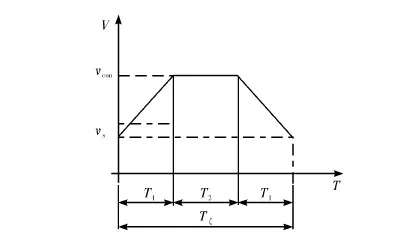
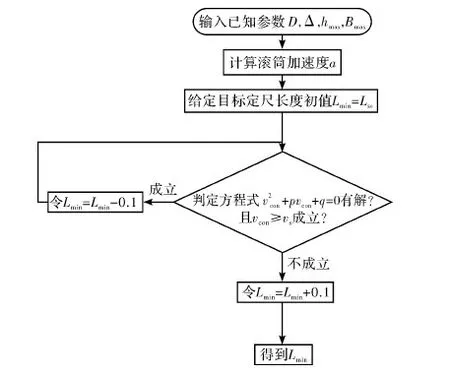
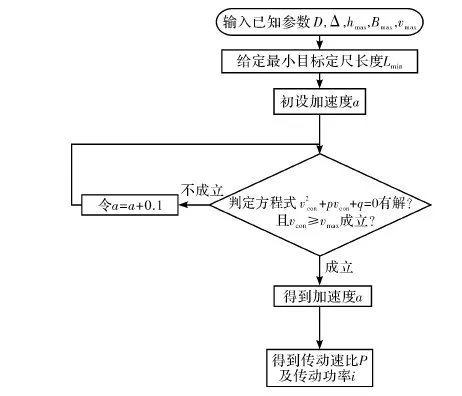
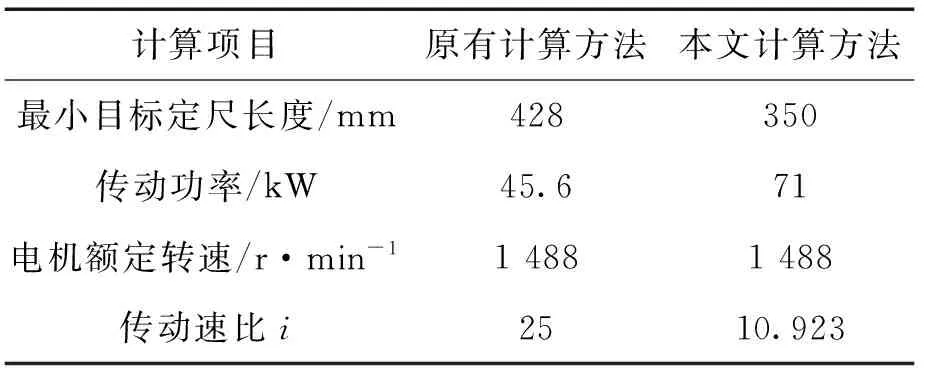
当目标定尺长度Ls 则,滚筒速度可调角域ξ为加速角α和制动角φ之和,即 ξ=α+φ 滚筒速度可调位域Ψ为 滚筒速度可调时域Tξ为 (5) 2.2最大目标定尺长度Lmax计算 为了得到最大目标定尺长度,第一刀剪切后,滚筒必须先降速,保持匀速,再升速到剪切速度,进行第二刀剪切。即第一刀剪切完成后,滚筒转动线速度从νs降速到νcon,降速时间为T1;保持匀速运行,运行时间T2,线速度再从vcon升速到vs,升速时间为T1,然后进行第二刀剪切,完成定尺剪切,如图3所示。 图3 最大目标定尺剪切速度变化曲线 则 (6) Tξ=2T1+T2 (7) (8) 式(6)、(7)代入式(8)得到 整理得到方程式 (9) 求解得到 设 p=Tξa-2νs 则方程式(9)变形为 此方程对称轴为νcon=-0.5p。 求解 同时,必须满足 0≤νcon≤νs (10) 方程有解,且式(10)满足的最大Lmax即为最大目标定尺长度,如图4所示为计算流程。 图4 最大目标定尺长度计算流程图 (1)输入各已知参数,D,Δ,hmax,Bmax,νmax等; (3)给定最大目标定尺长度初值Lmax=Ls0; (5)令Lmax=Lmax+0.1,转到步骤(3)重新计算,直到方程无解,或者判别式0≤νcon≤νs不成立; (6)令Lmax=Lmax-0.1,得到最大目标定尺长度。 2.3 最小目标定尺长度计算 为了得到最小目标定尺长度,第一刀剪切后,滚筒必须先升速,保持匀速,再减速到剪切速度,进行第二刀剪切。即第一刀剪切完成后,滚筒转动线速度从νs升速到νcon,升速时间为T1;保持匀速运行时间T2,线速度再从νcon降速到νs,降速时间为T1,然后进行第二刀剪切,完成定尺剪切,如图5所示。 图5 最小目标定尺剪切速度变化曲线 则 (11) Tξ=2T1+T2 (12) (13) 式(11)、(12)代入式(13)得到 整理 (14) 求解得到 设: p=-(Tξa+2νs) 方程式(14)变形得到 此方程对称轴为νcon=-0.5p>0。 求解得到 同时,必须满足 νcon≥νs (15) 方程有解,且式(15)满足的最小Lmin即为最小目标定尺长度,如图6所示为计算流程。 图6 最小目标定尺长度计算流程图 (1)输入各已知参数D,Δ,hmax,Bmax,νmax等; (3)给定最小目标定尺长度初值Lmin=Ls0; (5)令Lmin=Lmin-0.1,转到步骤(3)重新计算,直到方程无解,或者判别式νcon≥νs不成立; (6)令Lmin=Lmin+0.1,得到最小目标定尺长度。 式(3)、式(4)的飞剪传动设计参数计算的前提是:按照启停工作制,飞剪位于零位,从静止开始加速,到剪刃接触带钢时,加速到剪切速度,剪切完成后,飞剪开始减速,到零位时,减速到静止。 上述计算前提忽略了飞剪连续定尺剪切时,目标定尺长度对传动功率P及传动速比i的要求。 最大目标定尺长度Lmax的大小取决于匀速段速度νcon及其保持时间T2。当νcon=0,T2任意保持时,理论上可以得到任意的最大目标定尺长度Lmax。 最小目标定尺长度Lmin的大小取决于匀速段速度νcon及其保持时间T2。νcon越大,T2越大,Lmin越小,这就要求更大的滚筒加速度a。 得到滚筒加速度a后,传动速比i及传动功率P (16) (17) 计算步骤如图7所示。 图7 基于最小目标定尺长度的滚筒飞 剪传动设计参数计算流程图 (1)输入各已知参数,D,Δ,hmax,Bmax,νmax等; (2)给定最小目标定尺长度Lmin; (5)令a=a+0.1,转到步骤(4)重新计算,直到方程有解,且判别式νcon>νmax成立; (6)得到加速度值a,按照式(16)、(17)计算飞剪传动速比及传动功率。 通过采用本文所提出的基于最小目标定尺长度的滚筒飞剪传动设计参数计算方法对某汽车板重卷检查机组的滚筒式飞剪机传动设计参数进行计算分析。滚筒飞剪结构参数及工艺参数如下:滚筒直径D=321.5 mm,剪刃长度L=2 100 mm,Δ=1.5 mm,飞剪换算到电机轴上的飞轮矩GD2=2.17 kgf·m2。剪切带钢最大宽度Bmax=2 030 mm,最大厚度hmax=2.5 mm。最大剪切速度νmax=60 m/min,要求最小目标定尺长度为350 mm。主要计算结果如表1所示。 表1 传动设计参数计算结果比较 可见,考虑最小目标定尺长度时,传动功率有较大的增大,传动速比有较大地减小。 而原有计算方法得到的传动设计参数能够实现的最小目标定尺长度为428 mm。 本文在滚筒飞剪原有传动参数计算方法基础上,考虑了连续工作制时,用户要求的最小目标定尺长度对传动设计参数的影响。深入研究了滚筒飞剪连续定尺剪切原理,分别建立了基本定尺长度计算模型、最小目标定尺长度计算模型及最大目标定尺长度计算模型。形成比较完善的基于最小目标定尺长度的滚筒飞剪传动设计参数计算方法。并以某汽车板重卷检查机组的滚筒式飞剪机为例,进行了仿真计算,计算速度快,精度高,完全满足工程需要。 [1] 周国盈. 带钢精整设备[M]. 北京:机械工业出版社,1979. [2] 柳冉,蒋继中. 滚筒机构螺旋剪刃飞剪机静态剪切力计算公式探讨[J]. 重型机械, 2001,(03): 51-55. [3] 崔志昌,李松江. 滚筒式飞剪的设计与结构分析[J]. 机械设计与制造, 2005,(10): 42-44. [4] 汪建春,刘旺. 异周速双滚筒切头飞剪结构特点及分析[J]. 重型机械, 2007,(04):35-43. [5] 赵华国,刘文武. 滚筒式切头飞剪在剪切过程中里能参数的变化[J].一重技术,2002(04): 1-4. [6] 高秀华,李晓峰,王同建等. 双滚筒式切头飞剪剪切力的计算及计算机模拟[J]. 吉林工业大学自然科学学报.1999,29(03):18-23. [7] 邹家祥. 轧钢机械[M]. 北京:冶金工业出版社,2005. [8] 刘海昌. 新型板带飞剪机的设计. 机械设计与制造,2007(09):123-124. [9] 柳冉. 滚筒类飞剪机螺旋剪刃设计:中国:1220927A[P].1999-6-30. [10] 柳冉,胡光华. 按工艺要求直接求飞剪机构参数[J].重型机械,1996,31(12):62-66. [11] 张永虎. 钢板定长剪切系统的研究和设计[D].沈阳:沈阳理工大学,2008. [12] 鄂世伟,胡高举,王宇.滚筒飞剪剪切力计算研究[J]. 重庆工学院学报(自然科学版),2007,21(07):45-49 Calculation method of driving design parameters in drum shear WU Yong-jie1,YAN Sheng2,SUN Ya-bo1,CUI Wei-hua1 (1.China National Heavy Machinery Research Institute Co.,Ltd.,Xi’an 710032,China 2.Guangxi Liuzhou Iron and Steel Group Company Limited,Liuzhou 545000,China) This paper researched the influence of the minimum target cut length on driving design parameters, it established a calculation model of the target cut length, which formed a comparatively complete calculation method of driving design parameters in drum shear. This method is according to the principle of continuous specific cut length, the basis of the original driving parameter calculation method of drum shear was also considered. It took the drum shear of an auto strip coiling and inspecting line as an example, the simulation calculation was carried out. The results showed that the driving power of the drum shear increased and the transmission ratio decreased when the minimum target cut length was considered. drum shear;continuous working system;minimum target cut length;driving design parameter TG333 A 1001-196X(2017)05-0064-06 2017-04-23; 2017-05-26 2016年度陕西省重点科技创新团队计划项目(2016KCT-08) 吴永杰(1973-),男,高级工程师,从事板带精整及处理专业。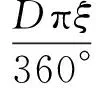
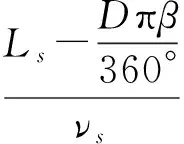
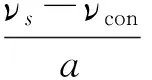
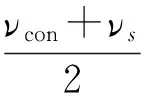
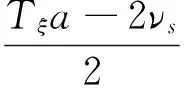
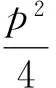
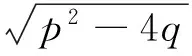
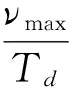
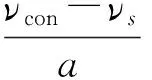
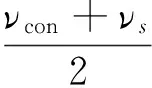
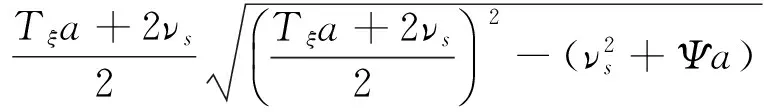
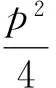
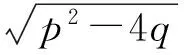
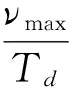
3 基于最小目标定尺长度的飞剪传动设计参数计算
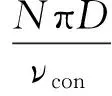
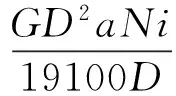
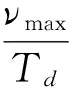
4 算例
5 结论

