基于PCRLB的目标跟踪节点选择算法
庞小双,王邢波
(南京邮电大学 自动化学院,江苏 南京 210023)
基于PCRLB的目标跟踪节点选择算法
庞小双,王邢波
(南京邮电大学 自动化学院,江苏 南京 210023)
针对能量、带宽、存储等资源限制的无线传感器网络下的目标跟踪问题,提出了基于扩展H∞滤波的后验-克拉美罗下界(PCRLB)传感器节点的选择算法。该算法可随时间动态选择一个最优传感器集合并将均方根误差(RMSE)作为优化目标跟踪的性能。无线传感器网络中对于非线性、非高斯的动态系统,采用蒙特卡罗方法计算基于状态估计误差的一步向前Cramer-Rao下界,利用扩展H∞滤波器对目标状态和PCRLB进行逼近估计,并以此作为传感器节点选择标准以实现传感器的在线选择。基于Matlab工具箱的计算机仿真结果表明,相对于随机传感器节点选择算法和基于最近邻的传感器节点选择算法,基于后验-克拉美罗下界的目标跟踪传感器观测节点选择算法具有更好的有效性和优越性。
目标跟踪;节点选择;均方根误差;后验-克拉美罗下界;扩展H∞滤波;无线传感器网络
1 概 述
近年来,随着传感器技术、无线通信技术、低功耗技术和嵌入式操作系统技术的不断发展,人们发现可以将传感器模块、数据采集模块、信息处理模块和无线通信模块等集成在一个体积很小的器件上,即传感器,并利用电池供电。无线传感器网络是由大量低成本、低功耗的传感器以自组织和多跳的方式构成的无线网络,WSN中的传感器通过无线通信的方式进行信息之间的传递,能够协作地感知、采集、处理和传输网络区域内被感知对象的信息,并最终把这些有用的信息发送给需要信息的用户。所以WSN被广泛应用于军事、智能交通、环境监控和医疗卫生等多个领域,但是其中目标跟踪是无线传感器网络最具代表性的应用之一[1-4]。由于WSN的能量、带宽、存储等资源的限制,为了充分发挥WSN的优势,必须在条件允许下,动态地选择一组最优的传感器节点参与目标跟踪,在满足跟踪性能要求的同时尽可能降低WSN的能量消耗。在目标跟踪过程中,为了尽可能准确地跟踪机动目标运动轨迹,就必须选择较多的传感器节点的信息,但是大量传感器的参与必然造成能量消耗的增加。那么选择一个最优的传感器节点集合在跟踪精度和能量消耗之间进行折中就变得至关重要。而传感器节点选择算法也称为传感器节点调度方法[5-7],可以在网络的能量消耗和目标的跟踪精度之间进行权衡。
传感器节点选择问题在各种应用中出现。例如,文献[8]提出了基于熵的传感器选择方法。随机传感器节点选择算法介绍了传感器调度和传感器覆盖率[9]。赵峰等[10]在传感器协作网络中提供了一种信息驱动传感器选择策略。更多的传感器网络选择方法在文献[11]用信息论的方法作为传感器的选择标准,例如基于信息熵、相对熵以及马氏距离等信息度量方法作为传感器选择的目标函数。Kalman滤波算法中经常使用基于估计误差协方差矩阵以及它的迹或行列式的信息度量方法进行传感器选择,例如Kaplan等[12]提出了全局传感器节点选择方法,并通过最小化期望后验滤波均方误差来选择最合适的传感器节点集合。
在系统信息模型和噪声统计特性已知的前提下,卡尔曼滤波技术能提供较好的估计结果。自20世纪60年代诞生以来,卡尔曼滤波在航天与航空领域都取得了巨大的成功。但在20世纪70年代,人们尝试将Kalman滤波运用到更普通的工业运用中,但很快就暴露出卡尔曼滤波潜在的假设与工业状态估计问题之间存在严重的不匹配问题。在该问题中,系统的精确模型和噪声的统计特性都很难获取。在此背景下,急需开发出一项能应对建模误差和噪声不确定性的扩展和滤波技术,于是相关研究的重点转向适用于这类问题的具有“鲁棒性”的滤波器。尽管可以设计基于卡尔曼滤波的鲁棒滤波器,但这仅是对现有方法的修正,而H∞滤波是专门为鲁棒性设计的。在外部扰动信号统计特性未知和系统模型存在参数不确定性的情况下,H∞滤波算法比Kalman滤波算法具有更好的鲁棒性,因此近几十年里H∞滤波问题得到了人们的特别关注[13]。除了能量有界外,H∞滤波对外部扰动信号的统计特性不做任何假设,只是使最坏扰动情况下的估计误差最小。
后验-克拉美罗下界(PCRLB)是目标状态估计误差下界,是传感器观测节点的最佳估计效果。不仅如此,它还表示目标跟踪过程中的一个性能边界。因此,将其作为传感器观测节点的管理准则是合理且可行的。由于该管理准则与滤波器的误差有关,因此可以将表示X方向位置和Y方向位置的PCRLB矩阵的迹应用于扩展H∞滤波,并以此作为传感器观测节点选择的管理准则。据此提出了基于PCRLB的目标跟踪的传感器观测节点选择算法。
2 系统模型
2.1目标运动模型
为简单起见,只考虑二维X-Y平面内的单目标跟踪问题。这里假设目标做近似匀速直线运动,速度为v,目标在k时刻的位置为s(k),那么经过采样时间T目标位置发生变化。目标运动过程中受到的随机扰动为wk,可以将系统表示为:
xk+1=Fkxk+Gkwk
(1)
其中,Fk为系统的状态转移矩阵;Gk为过程噪声矩阵;xk表示运动系统的状态向量,包括x方向的位置、y方向的位置、x方向的速度和y方向的速度,状态向量可以表示为:
xk=[x(k),y(k),vx(k),vy(k)]
(2)
其中,wk、vk是噪声项,这些噪声可能是随机的,且统计特性未知,也可能是确定的,均值可能非零。
2.2传感器节点测量模型
根据运动量测值(如方位、频率、距离等)对目标进行跟踪,是目标运动分析领域中的一个经典问题,在很多应用场合可以获得较为精确的距离信息。例如,在水下弹道测量系统中,水听器测量脉冲到达时刻获得待测目标的距离,可以采用多传感器对目标进行纯距离跟踪定位。因此,研究仅利用距离信息进行目标跟踪具有十分重要的作用。令hi表示tk时刻运动目标真实位置与传感器节点i之间的真实距离,则hi表示为:

(3)
其中,(xi,yi)表示传感器节点i的位置坐标;(x(k),y(k))表示tk时刻运动目标未知位置坐标。

(4)

3 基于扩展H∞滤波的无线传感器网络目标跟踪

yk=h(xk)+vk
(5)
H∞滤波问题的目标是估计状态的线性组合,换言之,想要估计zk,其表达式为:
zk=Lkxk
(6)

J=
(7)

(8)
其中,γ是用户指定的性能边界,重新整理方程后得到:
(9)
基于扩展H∞滤波的目标状态估计过程主要分为两步:
1)状态预测:利用系统的目标运动模型预测下一时刻系统的状态。
(1)一步向前推算状态预测。

(10)
(2)一步向前推算误差协方差。
(11)
2)状态修正。
(1)计算Kalman增益。
(12)
(2)由观测向量更新估计。
(13)
(3)更新误差协方差。

(14)
其中

(15)

扩展H∞滤波非常类似于传统的扩展卡尔曼滤波算法的形式,主要区别在于方程中不定协方差和黎卡提微分方程的出现。
3.1目标跟踪Cramer-Rao下界

(16)

(17)
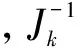
Tichavsky等[14]提出一种递归方法来计算一般多维离散非线性滤波后Cramer-Rao下界Jk的问题。估计基于k时刻之前(包括k时刻)量测值条件下的z1:k,那么k+1时刻的目标状态估计xk+1的Fisher信息矩阵计算如下:
(18)

3.2类似Fisher信息矩阵

(19)

(20)
可以通过降低随机参数Cramer-Rao下界来提高参数估计精度。Pk|k的公式可以改写成下列类似Fisher信息矩阵的形式:
Jf,k=Jp,k+Jl,k+Jz,k
(21)


(22)
Jk=
(23)
(24)
根据一步向前后验Cramer-Rao下界的状态估计方法对目标进行状态估计。
3.3基于PCRLB的传感器节点选择方法
传感器节点选择算法的最终目的就是可以随时间动态地选择一个最优的传感器集合优化均方根误差(RMSE),准确估计出目标的运动轨迹,而PCRLB矩阵又是直接与目标位置估计误差的均方根误差有关,所以定义一个目标函数,选择一种方法来寻找最小化期望均方根位置误差,依据后验费舍尔信息矩阵[15-16]表示如下:

(25)

(26)


(27)


(28)
那么,由式(27)、(28)可以看出,该算法对信息矩阵的运算可以转化为对矩阵行列式的计算,大大减少了计算量,降低了复杂度。只需在候选传感器集合中选择一个可以使信息度量C'最大的子集S,表达式如下:
(29)
4 仿 真
利用Matlab,分别对基于随机传感器选择、基于目标预测位置最近邻的传感器选择和基于扩展H∞滤波的PCRLB这三种方法进行仿真,比较各种方法的跟踪精度和能量消耗。
4.1仿真结果


P0|0=I4
其中,I4表示4*4的单位阵。Monte Carlo仿真次数为100。
利用扩展H∞滤波得到的代数Riccati方程的迭代计算依赖于标量γ和矩阵L的选取。L的选取影响到算法的计算复杂度,因此,需选择一个使Riccati方程计算复杂度最小的L参与跟踪过程,L=[1,1,1,1]。其中代数Riccati方程的γ值可以通过反复的仿真实验来近似确定。如图1所示,采用不同的γ值:γ2=2,γ2=10,γ2=100,如图2和图3所示,对由不同的γ值得到的X方向和Y方向的均方根误差进行比较,最后选择γ2=100。

图1 目标运动的真实轨迹和利用不同的γ得到的估计轨迹

图2 X方向的均方根误差

图3 Y方向的均方根误差
4.2与其他传感器节点选择算法的比较

(2)最近邻节点选择方法:当目标进入监测区域后,多个传感器节点感知到运动目标。基于目标预测位置最近邻方法选择下一时刻的簇集头节点。目标跟踪内的簇集头节点选择与其位置范围内最近的节点作为任务节点观测目标位置,并采用扩展H∞滤波完成目标的状态估计。
在以下实验中,单个目标从位置(1.0,1.0)开始运动,传感器进行实时跟踪。过程噪声wk对应的目标的噪声加速度,也被认为是一个未知的有界扰动能量。
图4显示了利用这三种算法得到的跟踪结果,分别描述了这三种传感器选择方法各自的目标运动轨迹。

图4 目标的真实轨迹和利用不同的传感器节点选择算法得到的估计轨迹
进行多次实验后取平均值,依据仿真结果,可以看出基于扩展H∞滤波的PCRLB传感器节点选择算法相对于随机分布的节点选择算法和KNN传感器选择算法,得到的目标运动轨迹最接近于真实的目标估计,具有较高的目标跟踪精度。这是因为PCRLB传感器节点选择算法是以已经获得的真实测量信息为前提,并且利用的信息是目标运动轨迹的真实信息,因此能选择更好的传感器节点进行目标跟踪,获得最优的传感器性能,充分发挥传感器网络的优势。
仿真实验还进一步利用目标位置估计误差的RMSE来评价这些算法的性能。位置均方根误差是指目标真实的和估计的X、Y方向的均方根误差。该值是一个标量,如果目标真实位置与估计位置重合,其值为0;如果目标的估计位置偏离真实位置,其值增大。在比较各种滤波算法的性能时,该值越小,表明算法的滤波精度越高。位置均方根误差定义如下:

(30)
其中,N为滤波过程中的采样次数;x、y分别表示目标位置在X方向的分量和Y方向的分量。
图5和图6分别显示了这三种算法在X方向和Y方向的RMSE。
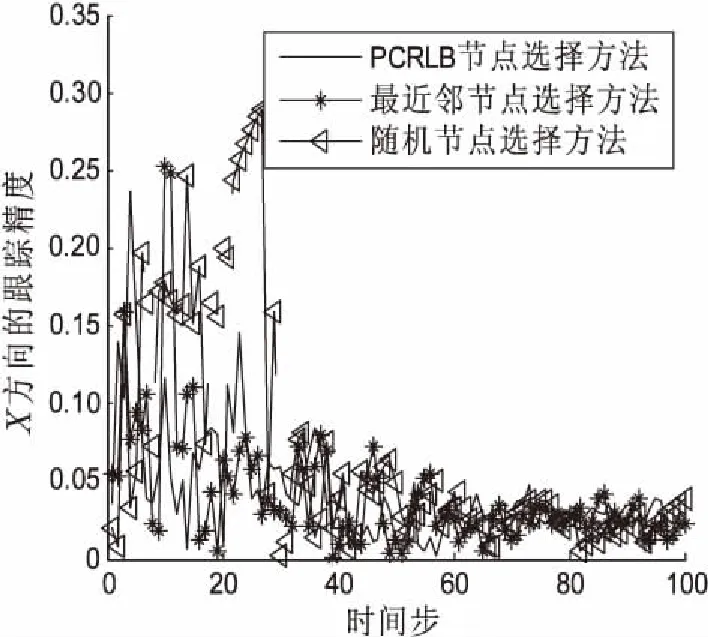
图5 不同目标跟踪传感器节点选择方法在X方向上的均方根误差比较

图6 不同目标跟踪传感器节点选择方法在Y方向上的均方根误差比较
可以看出,基于PCRLB的传感器节点选择算法能选择一组最优的传感器观测节点集合,获得更精准的目标跟踪估计,而且估计出的状态具有较小的均方根误差。在计算过程中为了避免涉入有矩阵的计算,增加算法的复杂度,将其转化为标量对矩阵行列式的计算。传感器节点选择算法必须在跟踪精度和能量消耗之间进行权衡。
5 结束语
目标跟踪传感器选择问题的任务是用由N个传感器节点组成的无线传感器网络对一个运动目标进行实时跟踪,但是为了减少网络的能量消耗和成本,只需要从这N个传感器节点中选择出M个进行目标跟踪。PCRLB给出了目标状态估计的一步向前预测均方根误差下界,对传感器网络下的目标跟踪问题,提出一种基于扩展H∞滤波的后验-克拉美罗下界的传感器选择方法。对于资源受限的无线传感器网络,通过对观测数据的量化处理和传感器节点选择,激活一组最优的传感器节点集合参与目标跟踪,权衡网络能量消耗和跟踪精度,有限管理网络资源。后续的研究可以将该方法应用到多目标跟踪传感器选择和分布式选择方法中。
[1] 孙利民,李建中,陈 渝,等.无线传感器网络[M].北京:清华大学出版社,2005.
[2] 官 理.无线传感器网络及其应用研究[J].电脑与电信,2008(2):13-14.
[3] 刘 博.无线传感网络中的目标跟踪技术[J].中兴通讯技术,2008(1):48-50.
[4] 孙晓艳.无线传感器网络目标跟踪问题研究[D].西安:西安电子科技大学,2011.
[5] 康 波,柯 欣,孙利民,等.无线传感器网络中的调度算法研究[J].计算机科学,2008,35(2):47-51.
[6] 胡湘华,杨学军.传感网节点调度方法综述[J].计算机工程与科学,2008,30(3):93-96.
[7] 李 丛.无线传感器网络中基于节点协作的目标跟踪算法研究[D].长沙:中南大学,2011.
[8] Wang H,Yao K,Pottie G,et al.Entropy-based sensor selection heuristic for target localization[C]//Proceedings of the 3rd international symposium on information processing in sensor networks.[s.l.]:ACM,2004:36-45.
[9] Gupta V,Chung T H,Hassibi B,et al.On a stochastic sensor selection algorithm with applications in sensor scheduling and sensor coverage[J].Automatica,2006,42(2):251-260.
[10] Zhao F,Shin J,Reich J.Information-driven dynamic sensor collaboration[J].IEEE Signal Processing Magazine,2002,19(2):61-72.
[11] Zhao F,Guibas L J.Wireless sensor networks:an information processing approach[M].San Francisco,CA,USA:Morgan Kaufmann,2004.
[12] Kaplan L M.Global node selection for localization in a distributed sensor network[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):113-135.
[13] Simon D.Optimal state estimation:Kalman,H∞and nonlinear approaches[M].Hoboken,NJ:John Wiley &Sons,2006.
[14] Tichavsky P,Muravchik C H,Nehorai A.Posterior Cramér-Rao bounds for discrete-time nonlinear filtering[J].IEEE Transactions on Signal Processing,1998,46(5):1386-1396.
[15] Zuo L,Niu R,Varshney P K.Posterior CRLB based sensor selection for target tracking in sensor networks[C]//International conference on acoustics, speech and signal processing.[s.l.]:IEEE,2007.
[16] Mohammadi A,Asif A.Consensus-based distributed dynamic sensor selection in decentralised sensor networks using the posterior Cramér-Rao lower bound[J].Signal Processing,2015,108:558-575.
SensorSelectionAlgorithmforTargetTrackingwithPCRLB
PANG Xiao-shuang,WANG Xing-bo
(College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
For target tracking problems limited by resources like energy,bandwidth and storage under wireless sensor networks,a kind of sensor selection algorithm of Posterior Cramer-Rao Lower Bound (PCRLB) based on the extendedH∞filter is proposed,which can select an optimal sensor set dynamically with time and optimize tracking performance in terms of Root Mean Square Error (RMSE).Monte Carlo method is adopted to compute one-step look-ahead CRLB on the state estimation error in a nonlinear,possibly non-Gaussian and dynamic system with extendedH∞filter for approximate estimation of target state and PCRLB which are presented as the sensor selection criterion to realize the sensor options online.Simulation results with Matlab toolbox show that it has owned better effectiveness and superiority than stochastic sensor node selection algorithm and sensor node selection algorithm based on nearest neighbor.
target tracking;sensor selection;RMSE;PCRLB;extendedH∞filter;wireless sensor network
TP301.6
A
1673-629X(2017)10-0054-06
2016-10-08
2017-01-17 < class="emphasis_bold">网络出版时间
时间:2017-07-11
国家自然科学基金杰出青年基金(60825304);国家“973”重点基础研究发展计划项目(2009cb320600)
庞小双(1991-),女,硕士研究生,研究方向为无线传感器网络、目标跟踪;王邢波,博士,讲师,硕士生导师,研究方向为无线传感器网络、目标跟踪、机器人控制。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1455.046.html
10.3969/j.issn.1673-629X.2017.10.012

