无限狄利克雷混合模型的变分学习

曾凡锋，陈 可，王宝成，肖 珂

(北方工业大学，北京 100144)

无限狄利克雷混合模型的变分学习

曾凡锋，陈 可，王宝成，肖 珂

(北方工业大学，北京 100144)

有限高斯混合模型广泛应用于模式识别、机器学习和数据挖掘等领域，但现实中的许多数据都具有非高斯性，而高斯混合模型无法准确地描述这些数据。此外，有限高斯混合模型还存在参数估计和模型选择困难的问题。为了更好地拟合非高斯数据，解决有限高斯混合模型的参数估计和模型选择困难的问题，在研究一种适合于建模非高斯数据的无限狄利克雷混合模型的学习方法的基础上，提出了一种高效的变分近似推理算法。该算法能够同时解决参数估计及模型选择的问题。为了验证该算法的有效性，在合成数据集上进行了大量实验。验证实验结果表明，该算法能够很好地解决模型选择及参数估计的问题。所提出的无限狄利克雷混合模型还可应用于目标检测、文本分类、图像分类等方面。

狄利克雷；无限混合模型；变分贝叶斯；模型选择；参数估计

1 概 述

有限混合模型[1-2]是分析复杂数据的一个简便和优秀的概率建模工具，它可以通过使用多个分量描述一个复杂的数据分布。其中，高斯混合模型具有便于学习、形式简单和描述能力强、聚类精度高等优点，成为研究最为深入的有限混合模型，在模式识别、机器学习、统计模型、计算机视觉以及数据挖掘等领域应用广泛[3]。文献[4]利用高斯混合模型建模研究预测智能控制交通、辅助驾驶系统、军事数字化战场中移动对象的不确定性轨迹。文献[5]利用高斯混合模型对含有非视距误差信息进行定位估计。文献[6]将混合模型应用于文本主题-情感分析中。然而，实际中，许多具有非线性、非高斯性、有界性以及非对称性的数据，均无法用高斯混合模型准确拟合[7]。近期的研究表明，非高斯混合模型能够有效拟合非高斯数据。目前大量关于非高斯混合模型的研究成果相继涌现，比如有限贝塔刘维尔混合模型，能有效地应用于图像场景分类[8]、人体肤色检测[9]中。文献[10]提出了混合逆狄利克雷混合模型，并成功应用于正的非高斯数据聚类。然而，有限混合模型需要对混合分量数进行估计和确定，分量数的过多或过少会引起模型的过拟合或欠拟合问题。

相对于有限混合模型，无限混合模型直接避开了分量数的选择，优化了模型拟合度。无限混合模型的研究主要涉及参数估计的问题。参数估计常被称为参数学习。参数学习方法主要分为两大类：确定性学习算法和非确定性学习算法。其中确定性学习算法以极大似然估计(Maximum Likelihood Estimation，MLE)的EM算法为主，主要是通过优化模型似然函数来求模型参数的估计值。EM算法存在估计过程陷入局部最优、估计结果严重依赖初始化值[11]和出现过拟合或欠拟合等问题。非确定性学习算法以马尔可夫蒙特卡罗(Markov Chain Monte Carlo,MCMC)链为代表的贝叶斯学习算法为主。贝叶斯估计法先利用样本数据将模型参数的先验概率密度通过贝叶斯定理转变为后验概率密度，然后用后验概率密度估计模型参数。然而，贝叶斯估计法存在高维密度积分的问题。目前，解决高维数积分困难问题的主要方法是随机近似和确定性近似的方法[12]。随机近似法主要有MCMC抽样算法，但其存在收敛速度缓慢、局限于小规模数据集环境以及收敛不确定性大等缺点；确定性近似法主要有拉普拉斯近似算法和变分贝叶斯算法。拉普拉斯近似算法对于单峰分布的模型有很好的近似功能，但是对多峰分布的模型其近似性能不理想，所以拉普拉斯近似算法推理得到的结果不准确。

变分贝叶斯是解决高维积分困难问题的一种重要的近似推理方法。其核心思想是利用易处理的一类分布族来逼近隐变量的后验分布，通过最大化变分参数的对数似然目标函数的下界获得模型参数的估计值[13]。变分贝叶斯能够适应高维的观测环境，且运算量较少，已经成为概率混合模型学习的主流方法。变分框架受到了广泛关注，并且能在各种应用中提供很好的泛化性能[14-17]，包括有限混合学习。而且变分学习框架在高斯混合模型中已被证明可以提供更好的参数估计[18-20]。

为此，针对无限狄利克雷混合模型的学习问题，提出一种有效的变分近似推理框架，该框架能够同时解决模型选择及参数估计的问题。

2 无限狄利克雷混合模型的变分学习

2.1无限狄利克雷混合模型

狄利克雷过程产生离散的随机分布，而狄利克雷过程混合模型则产生绝对连续分布[16-21]，无限狄利克雷混合模型可以看作具有无限个分量的混合模型，是具有狄利克雷过程先验假设的有限混合模型的极限形式[22]。在对非高斯数据进行建模时，混合分量数可以自动收敛。

有限狄利克雷混合模型定义为M个狄利克雷分布的线性组合，其表达式为：

(1)

狄利克雷分布的概率密度函数为：

(2)

其中，Γ()是伽马函数。

选择合适的M数量是混合模型选择的重要问题，可以假设M值是无限的[23]。当式(1)中的M值趋近于无穷大时，狄利克雷混合模型线性组合由有限变成无限，无限狄利克雷混合模型的表达式如下：

(3)

(4)

给定类标签，隐变量Z和参数α服从X的条件分布，则观测变量集X的条件分布为：

(5)

在贝叶斯推理中，需要预先指定模型参数的先验分布。因为狄利克雷分布的标准共轭先验不能直接用于贝叶斯推理，故采用Gamma分布作为它的近似共轭先验[8-9]。假设DMM中各个参数是统计独立的，则参数α的先验概率分布如下：

(6)

其中，(gmd,hmd)是超参数，且满足gmd>0,hmd>0。

2.2模型的变分学习

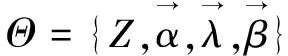
(7)

其中，<·>n≠s代表除了n=s之外的所有服从Qn(Θn)的期望。

根据文献[24-25]提出的变分推理方法，可以在M值上做一个变化分布的截断，比如：

(8)

其中，M是一个截断级，它是一个变化的参数，可以任意初始化，而且在变分学习过程中自动最优化。

理论上，棒断裂性表示方法可以以任意精度逼近真实分布。因此，通过采用棒断裂性表示和因式分解假设，可以获得参数集合的后验概率：

(9)

对每一个因子都使用式(7)，可以获取到变化后的后验概率的每一个因子的最优结果：

(10)

(11)

(12)

参数更新方程中的期望值如下：

=rnm

(13)

(14)

(15)

(16)

(17)

由于每一个变分因子的解是通过其他因子的期望值相互关联的，所以模型的优化可以通过一个类似期望最大化(EM)算法来实现，算法步骤如下：

(1)初始化分量数M，以及超参数gmd，hmd，am，bm的值；采用K-means算法初始化rnm的值。

(2)变分步骤：使用当前的模型参数分布估计式(13)～(17)的期望值。

(4)重复步骤(2)和(3)直至收敛。

(6)设定阈值为10-5，忽略混合系数接近小于阈值的分量并且检测最终的分量数。

3 实验结果及分析

为了验证提出的基于变分贝叶斯算法的无限狄利克雷混合模型(variational Infinite Dirichlet Mixture Model，varInDMM)的性能，在程序生成的合成数据集上，进行了大量的仿真实验。实验中分量数初始化值设定为15，设定狄利克雷混合模型的共轭先验概率(gmd,hmd)=(1,0.1)，并初始化混合权重等系数。

实验生成了四个合成数据集，四个合成数据集的数据可以指定分量数、维数且服从狄利克雷分布，利用四个合成数据集进行以下实验：

(1)对比提出的变分贝叶斯算法的无限狄利克雷混合模型与文献[20]中的变分贝叶斯算法的有限狄利克雷混合模型(variational finite Dirichlet Mixture Model，varDMM)的估计精度。该算法程序运行15次，结果取统计的平均值。表1量化地给出了变分贝叶斯算法的无限狄利克雷混合模型对于四个合成数据的参数估计结果。通过对比参数的真实值和varInDMM的参数估计结果发现，对于每一个数据集，利用varInDMM得到的估计值与真实值基本吻合。通过对比varInDMM与varDMM的参数估计结果可以看出，基于变分贝叶斯算法的无限狄利克雷混合模型的参数估计值更为精确。

(2)图1给出了变分贝叶斯算法对于四个合成数据集学习得到的概率密度图。

从图1可见，狄利克雷分布的概率密度函数既可以是对称的，也可以是非对称的，因此它对非高斯数据具有很强的描述能力。

图1 合成数据集变分学习后的混合密度

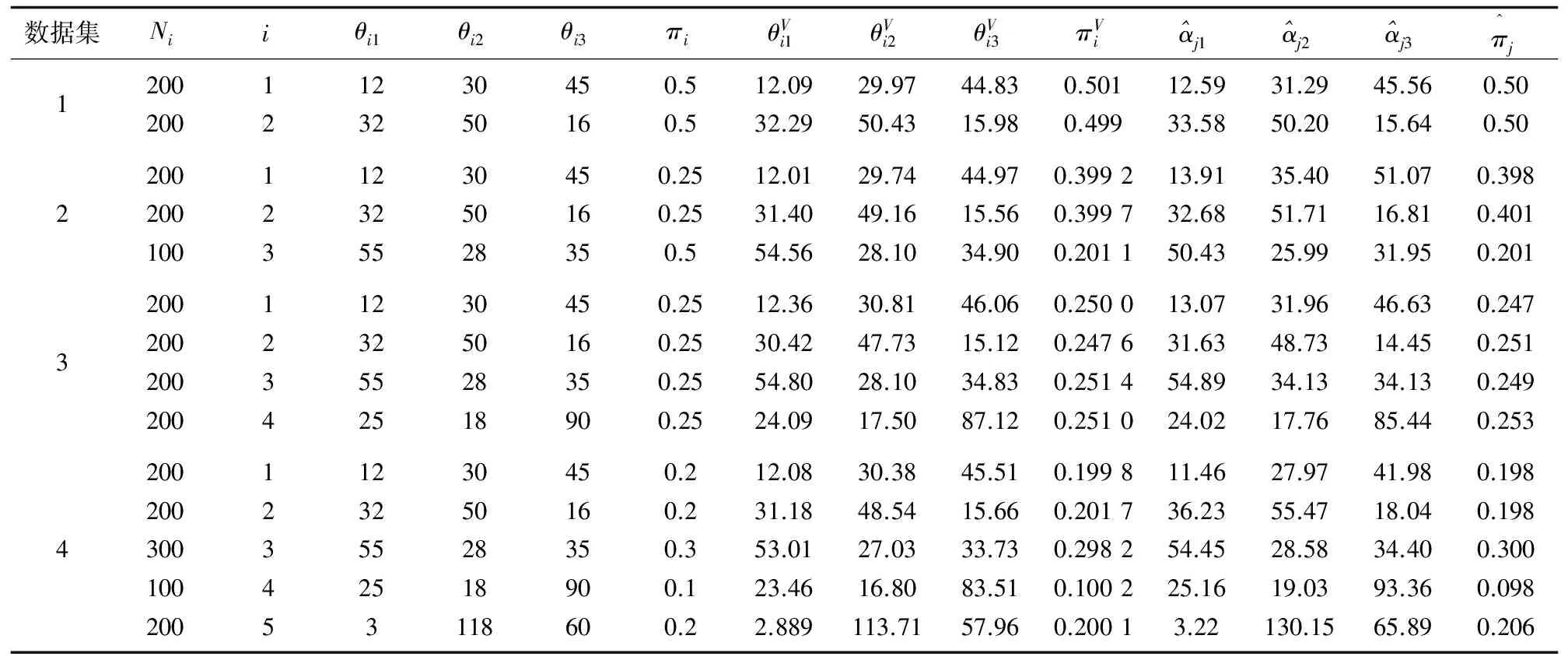
表1 不同合成数据集的参数

(3)对比varInDMM与varDMM的收敛速度，表2给出了两种算法对于四个合成数据集学习的收敛时间。由表2可见，提出的基于变分贝叶斯算法的无限狄利克雷混合模型具有更快的收敛速度。

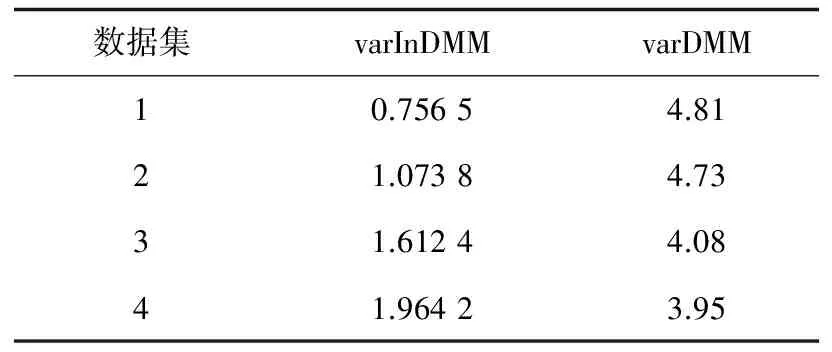
表2 算法的收敛时间 s

(4)算法初始化时定义的狄利克雷分量数为15。变分贝叶斯算法设置了隐变量，每一次的迭代循环中都会更新超参数，然后会重新计算各个分量的权值。若隐变量所指示分量出现权重过小的结果，该分量是冗余分量，加权求和时可忽略它的存在，即认为Znm=0。变分贝叶斯算法对于四个合成数据集的有效分量学习结果如图2所示。由此可见，该算法最终收敛后可以通过模型选择。

4 结束语

针对有限混合模型存在的参数估计和模型选择的问题，提出了一个变分推理框架来学习无限狄利克雷混合模型。仿真实验表明，文中算法能够有效地估计模型参数，同时确定混合分量数，避免了有限混合模型的模型选择困难问题。实验对比了变分学习的无限狄利克雷混合模型和有限狄利克雷混合模型的估计值，以及两种算法的收敛时间，证明了该算法在估计精度上更为精确，收敛速度更快。由合成数据集变分学习后的混合密度图可见，该模型可以很好地拟合非高斯数据。表明该算法是有效的和可行的。下一步工作将研究基于变分贝叶斯算法的无限狄利克雷混合模型的特征选择问题。

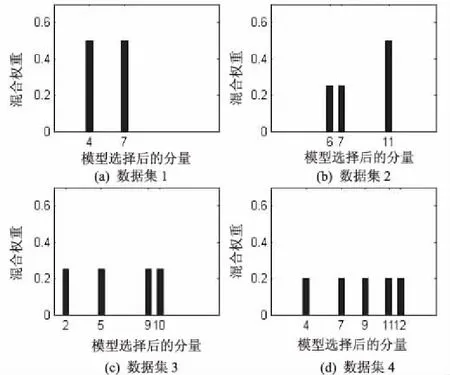
图2 模型选择后的有效分量

[1] Titterington D M，Smith A F M，Makov U E.Statistical analysis of finite mixture distributions[M].New York:Wiley,1985.

[2] Chen Tao,Zhang Jie.On-line multivariate statistical monitoring of batch processes using Gaussian mixture model[J].Computers & Chemical Engineering,2010,34(4):500-507.

[3] Lopez-Rubio E,Palomo E J.Growing hierarchical probabilistic self-organizing graphs[J].IEEE Transactions on Neural Networks,2011,22(7):997-1008.

[4] 乔少杰,金 琨,韩 楠,等.一种基于高斯混合模型的轨迹预测算法[J].软件学报,2015,26(5):1048-1063.

[5] 崔 玮,吴成东,张云洲,等.基于高斯混合模型的非视距定位算法[J].通信学报,2014,35(1):99-106.

[6] 樊 娜,蔡皖东,赵 煜.基于混合模型的文本主题-情感分析方法[J].华中科技大学学报:自然科学版,2010,38(1):31-34.

[7] Nguyen T M,Wu Q M J.Gaussian mixture model based spatial neighborhood relationships for pixel labeling problem[J].IEEE Transaction on System Man and Cybernetic,2012,42(1):193-202.

[8] 赖裕平,丁洪伟,周亚建,等.有限贝塔刘维尔混合模型的变分学习及其应用[J].电子学报,2014,42(7):1347-1352.

[9] Ma Zhanyu, Leijon A. Bayesian estimation of beta mixture models with variational inference[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(11):2160-2173.

[10] Bdiri T，Bouguila N.Positive vectors clustering using inverted Dirichlet finite mixture models[J].Expert Systems with Applications,2012,39(2):1869-1882.

[11] Biernacki C,Celeux G,Govaert G.Choosing starting values for the EM algorithm for getting the highest likelihood in nultivariate Gaussian mixture models[J].Computational Statistics and Data Analysis,2003,41(3-4):561-575.

[12] Grimmer J.An introduction to Bayesian inference via variational approximations[J].Political Analysis,2011,19(1):32-47.

[13] Bishop C M.Pattern recognition and machine learning[M].New York:Springer-Verlag,2006.

[14] Teschendorff A E,Wang Y,Barbosa-Morais N L,et al.A variational Bayesian mixture modelling framework for cluster analysis of gene-expression data[J].Bioinformatics,2005,21(13):3025-3033.

[15] Bali B,Mohammad-Djafari A.A variational Bayesian algorithm for BSS problem with hidden Gauss-Markov models for the sources[C]//Proc of ICA.[s.l.]:[s.n.],2007:137-144.

[16] Snoussi H, Mohammad-Djafari A. Estimation of structured Gaussian mixtures:the inverse EM algorithm[J].IEEE Transactions on Signal Processing,2007,55(7):3185-3191.

[17] Skolidis G,Sanguinetti G.Bayesian multitask classification with Gaussian process priors[J].IEEE Transactions on Neural Networks,2011,22(12):2011-2021.

[18] Wang B,Titterington D M.Convergence properties of a general algorithm for calculating variational Bayesian estimates for a normal mixture model[J].Bayesian Analysis,2006,1(3):625-650.

[19] Corduneanu A,Bishop C M.Variational Bayesian model selection for mixture distributions[C]//Proceedings of eighth international conference on artificial intelligence and statistics.[s.l.]:[s.n.],2001:27-34.

[20] Fan Wentao,Bouguila N,Ziou D.Variaional learning for finite Dirichlet mixture models and applications[J].IEEE Transaction on Neural Networks and Learning Systems,2012,23(5):762-774.

[21] 梅素玉,王 飞,周水庚.狄利克雷过程混合模型、扩展模型及应用[J].科学通报,2012,57(34):3243-3257.

[22] MacKay D,Peto L C B.A hierarchical Dirichlet language model[J].Natual Language Engineeing,1994,1(3):1-19.

[23] Bouguila N,Ziou D.A Dirichlet process mixture of Dirichlet distributions for classification and prediction[C]//IEEE workshop on machine learning for signal processing.[s.l.]:IEEE,2008:297-302.

[24] Ishwaran H,James L F.Gibbs sampling methods for stick-breaking priors[J].Journal of the American Statistical Association,2001,96(453):161-173.

[25] Blei D M, Jordan M I. Variational inference for Dirichlet process mixtures[J].Bayesian Analysis,2005,1(1):121-144.

VariationalLearningforInfiniteDirichletMixtureModel

ZENG Fan-feng，CHEN Ke，WANG Bao-cheng，XIAO Ke

(North China University of Technology,Beijing 100144,China)

Finite Gauss mixture model is widely used in pattern recognition,machine learning and data mining and so on,but many data in reality are non Gauss,which cannot accurately describe these data.In addition,there exist difficulties in parameter estimation and model selection in the finite Gauss mixture model.In order to better fit the non Gauss data and solve the problem of parameter estimation and model selection of the finite Gauss mixture model,on the basis of research on basic learning method of infinite Dirichlet mixture model suitable for modeling the data of a non Gauss,an efficient variational approximate inference algorithm is proposed,which solves problem of parameter estimation and model selection at the same time.In order to verify its validity,a lot of experiments are carried out on the synthetic data set.The experimental results show it can solve the problem of model selection and parameter estimation.Infinite Dirichlet mixture model proposed can also be applied to object detection,text classification,image classification and other parts.

Dirichlet;infinite mixture models;variational Bayes;model selection;parameter estimation

TP181

A

1673-629X(2017)10-0019-05

2016-10-10

2017-01-12 < class="emphasis_bold">网络出版时间

时间：2017-07-11

国家自然科学基金资助项目(61371142)；北方工业大学校内专项(XN060)

曾凡锋(1966-)，男，硕士，副研究员，研究方向为信息安全、图像处理、系统辨别等；陈 可(1991-)，男，硕士研究生，研究方向为信息安全、机器学习。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1455.048.html

10.3969/j.issn.1673-629X.2017.10.005