一种改进的特征点方向分配算法

贾 琪，王晓丹，周来恩，翟夕阳

(空军工程大学 防空反导学院，陕西 西安 710051)

一种改进的特征点方向分配算法

贾 琪，王晓丹，周来恩，翟夕阳

(空军工程大学 防空反导学院，陕西 西安 710051)

现有特征点方向分配算法易受噪声干扰，在光照、仿射变换时准确性有待提高。针对以上不足，在SIFT算法基础上，提出了一种改进的特征点方向分配算法。该算法以特征点为中心，在0°～360°的范围内固定角度间隔，等距采样若干局部区域的圆形图像小块，计算各圆形图像小块质心相对圆心的偏移值。根据统计学原理以及实验验证表明，低偏移值区域易受噪声干扰且对特征点主方向的确定没有影响。据此，改进算法排除低偏移值局部区域，计算剩余局部区域像素梯度的幅度与幅角，利用方向直方图给特征点分配主方向。结果表明，相比SIFT算法，改进算法在主方向分配时运行速度更快，同时准确性更高。此外，在特征点匹配实验中，对视角变换的数据集图像，改进算法的准确率与现有算法基本持平；在噪声干扰的数据集图像中，改进算法的准确率提升了17%。

特征点；方向分配；SIFT；梯度

1 概 述

图像点特征是图像的一种重要局部特征，它是计算机视觉、模式识别中重要的信息来源[1-2]。现有特征点描述算法中，特征点方向分配的重要性常被忽略[3-4]。特征点方向是指给定一个参考方向，可任意选择，当特征点局部图像发生旋转变换时，给定的参考方向同旋转变换方向保持一致，且对噪声及复杂背景变换等干扰具有鲁棒性。习惯上，将参考方向称为特征点的主方向。

目前，应用最广泛的当属SIFT算法[5]中的梯度方向分配算法，利用特征点局部区域的梯度分布特性，给特征点分配一个或多个主方向，取得了非常好的效果，但也存在一些不足。经统计分析可知，特征点主方向仅由部分局部区域的梯度决定。SIFT算法计算整个局部区域的梯度值，然后进行统计分析确定主方向，时间复杂度高，且易受外界干扰。DIFT算法[6]对特征点局部区域进行DCT变换，多次旋转局部图像，根据DCT域系数的比值确定主方向。HIPS算法[7]中提出一种高效的方向分配算法，以特征点为中心，仅计算特征点16个圆形邻域像素的梯度值，以抗干扰能力减弱为代价提升效率。SURF[8]、KAZE[9]中计算特征点局部区域的Harr小波特征，以特征点为中心滑动张角为π/3的扇形区域，取扇形区域内Harr小波特征总和值最大的方向为主方向，算法中计算Harr小波特征与特征值总和均需要时间开销，而离散化扇形旋转角度降低了算法准确性。Gauglitz等[10]提出了CoM(Center-of-Mass)和HoI(Histogram-of-Intensities)方向分配算法。CoM算法将特征点圆形局部区域视为有质量的点，计算质心，主方向取特征点至质心的方向。实验结果表明，质心距特征点较近时，主方向易受噪声干扰，准确性不佳。HoI算法同样选取特征点圆形局部区域，但以特征点为基准计算梯度的幅值、幅角，期间不使用双线性插值。相比SIFT算法，HoI算法将运行时间降低了一个数量级，代价是降低了算法准确性。

随着计算性能的提升，基于机器学习的特征点方向分配算法[11-12]也逐渐被提出。算法以不同角度旋转样本图像获取足够多的训练集数据，通过有监督学习训练模型，性能相比手工设计的主方向分配算法有进一步的提升，但也存在一些不足，如模型难以学习多种复杂变换共存的训练集数据，当图像存在多种复杂变换时，基于机器学习的特征点方向分配算法性能下降明显，算法鲁棒性有待提升，等等。为此，需要设计一种简单易行，能对干扰具有强鲁棒性，同时准确性高的方向分配算法。

在SIFT算法的基础上融合CoM算法，文中提出了一种改进的特征点方向分配算法，即在确定特征点主方向之前，通过一定策略排除特征点周围对主方向生成没有影响且易受干扰的局部区域，提升主方向分配的鲁棒性与准确性，并通过实验对该方法进行验证。

2 改进的特征点方向分配算法

2.1SIFT中特征点方向分配算法

SIFT，全称是尺度不变特征变换，是图像匹配时提取特征点的一种算法，同时也是计算机视觉中的一种局部特征描述子，能够很好地解决出现平移、光照、视角、旋转等变化的多幅图片之间的匹配问题。算法过程分为四步：尺度空间极值点检测、特征点定位、特征点方向分配、特征点描述。

SIFT中特征点方向分配算法的步骤为：首先，假定某个特征点所在尺度为σ，计算以该特征点为圆心，4.5σ为半径的圆形邻域内高斯图像的幅值和幅角，计算方法如下：

m(x,y)=

(1)

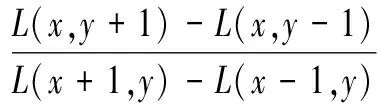
(2)

其中，m(x,y)表示图像梯度的幅值；θ(x,y)表示图像梯度的幅角；L表示关键点所在的尺度。

然后，对特征点邻域内像素点的梯度方向和幅值进行直方图统计。统计方法为在梯度方向0°～360°的范围划分36个区间，每个区间10°作为直方图的横轴，采用高斯加权将梯度幅值的累加作为直方图的纵轴，高斯加权是为了保证离中心越近的像素点梯度信息越重要。

最后，根据直方图统计结果，取峰值位置的横轴方向为特征点主方向，为了增强算法的鲁棒性，当存在有峰值80%能量以上的梯度方向，则分配给特征点作为辅方向。

特征点方向分配作为中间环节，其准确性对特征点描述具有较大影响。首先选取Oxford数据集中旋转、尺度变换的boat图片集，利用SIFT算法提取特征点并存储。随机选取300个特征点，将选取特征点的主方向以3°为步长递增，在0°～360°范围共生成120个主方向不同位置相同的特征点。最后，随机抽取100个特征点进行特征描述，以原特征点描述向量为基准，计算旋转不同角度的特征描述误差2-范数，取平均值为最终结果，结果如图1所示。其中，横坐标的正、负代表相对主方向逆、顺时针的角度差值。

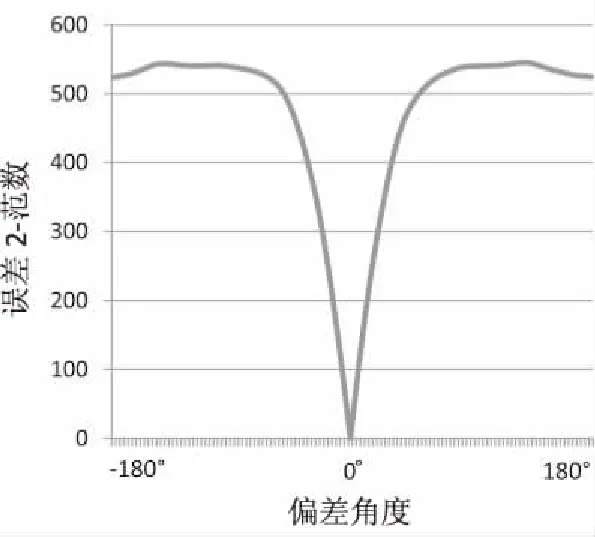
图1 不同主方向偏差角度下特征点的描述误差2-范数

由图1可知，当特征点主方向旋转3°时，描述误差的2-范数增加57.64，且随着旋转角度的增加急剧上升。由此可见，描述子中特征点方向分配的准确性对特征点描述具有较大影响。此外，文献[13]从图像旋转变换一致性的角度提出了一种特征点主方向修正算法，根据图像在旋转变换中各特征点主方向变换角度相等，通过分析SIFT、SURF中方向分配算法确定的各特征点主方向，估计图像的旋转角度，然后对分配的特征点主方向进行修正，在特征点匹配实验中取得了较好的效果，进一步证实了以上观点。

2.2CoM方向分配算法

CoM，全称是基于质心的方向分配算法，对特征点的微小移位及局部噪声干扰具有一定的鲁棒性。算法过程分为三步：特征点局部区域采样、局部区域质心计算、特征点主方向确定。

首先，采样半径为R的特征点圆形局部区域，R的取值直接影响算法的性能与效率。通过大量的对比实验，表明R为10.5时，性能与效率具有较好的折中比。

然后，计算特征点局部区域的质心，通过对比采用不同加权函数的算法，得到采用二次方程权函数能较好地平衡局部区域边缘与中心对结果取值的贡献，使计算结果更加平滑。二次方程权函数如下：

w(r)=1-(r/rmax)2

(3)

最后，将特征点至质心的方向作为主方向分配给特征点，CoM分配主方向给特征点的方法如图2所示。

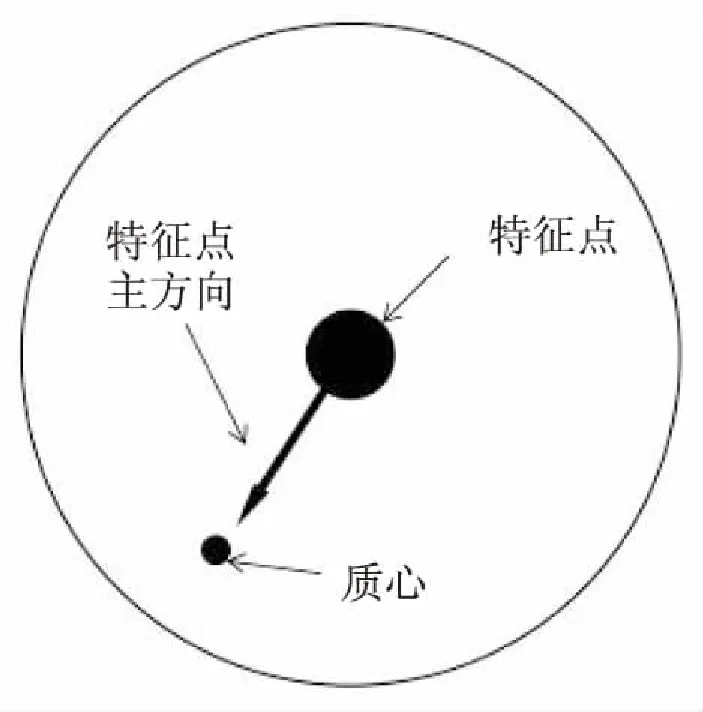
图2 CoM算法特征点的主方向分配

2.3改进算法主要步骤

2.3.1 特征点局部区域采样

特征点局部区域采样分为两步：特征点局部区域划分和圆形图像小块采样。

对于特征点局部区域划分，方法是在0°～360°的范围内，以固定角度间隔θ划分特征点所在区域，以θ取90°为例，划分方法如图3(a)所示。

图3 特征点局部区域采样方法

对于圆形图像小块采样，其方法是在特征点局部区域划分范围内，求解满足式(4)要求的圆心坐标。其中，假设圆形图像小块半径为R，(x,y)表示圆心坐标，(xp,yp)表示特征点坐标，θN表示第N个划分区域中过特征点的二分线方向。

(4)

实验表明，当N=4，R=3时，改进算法性能最佳。此时，以特征点为中心，局部区域如图3(b)所示。

实验中，为保证算法的准确性，去除靠近边缘不能完整采样的特征点，此类特征点约占总特征点数目的1%～3%，通常不稳定，去除后对算法几乎没有影响。2.3.2 特征点主方向确定

在局部区域采样的基础上，特征点主方向确定分为三个步骤：带权函数的质心计算、非低偏移值区域获取、特征点主方向确定。

首先，带权函数的质心计算方法借鉴CoM算法，为提升采样效率，提出改进策略：对不同角度间隔和图像小块半径的特征点需采样的邻域像素进行预处理，提前确定各像素相对特征点的偏移，省去中间计算过程。

其次，根据统计学原理并通过实验验证[10]，低偏移值区域易受噪声干扰且对特征点主方向的确定没有影响，改进算法排除了低偏移值区域，存储剩余区域的像素值供下一步计算使用。排除低偏移值区域后，重叠部分的像素不重复计算。

最后，计算剩余区域梯度的幅值、幅角，确定特征点方向直方图柱数，采用高斯加权将梯度幅值累加至对应方向的直方图柱中，取峰值方向及大于峰值80%能量的方向作为主方向。计算过程中，根据方向直方图柱数，对像素竖直、水平的幅值比建立幅角数组，简化幅角计算为查表操作，提升算法效率。

综上所述，假设改进算法参数θ=90°、R=3，其主要步骤如图4所示。

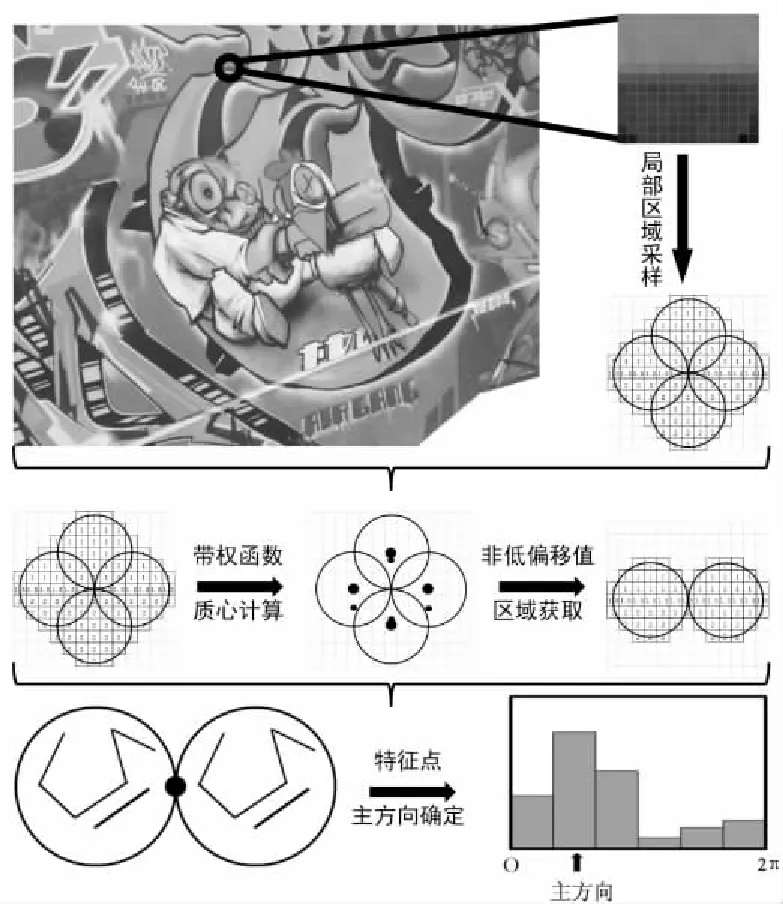
图4 改进算法主要步骤

改进的特征点方向分配算法流程为：

Step1：设有灰度图像I，利用特征点提取算法得到其特征点集P，满足(xp,yp)∈P；

Step2：分别采样集合P中特征点局部区域，剔除不满足要求的特征点，得到特征点局部区域集C与剩余特征点集P'。其中，特征点m(xp',yp')对应局部区域集合为Cm；

Step3：计算特征点局部区域集C的质心偏移值，去除低偏移值区域，得到C'；

Step4：利用改进策略，计算各特征点剩余局部区域集C'的梯度幅值与幅角，将计算得到的幅值与幅角分配到离散化的方向直方图中；

Step5：对方向直方图进行高斯平滑，解决因没有仿射不变性而产生的特征点不稳定的问题；

Step6：根据方向直方图的结果，分别给P'中特征点分配一个或多个主方向。

3 实 验

实验采用Ubuntu 10.4系统环境，PC机配置为Inter (R) i7-4790 3.60 GHz处理器，内存为8 G。选取Oxford数据集，由8组每组6张的800×640像素图片组成，包含对图像视角、旋转、噪声、图像压缩、尺度和光照等的变换。改进算法参数设置在Matlab 2014a软件环境下运行；特征点匹配实验中，特征描述子构造使用加载OPENCV 2.9.1开源库的VS 2010软件环境。

3.1改进算法参数设置

改进算法中共有三个参数需要设置，分别是划分角度间隔θ、图像小块半径R、低偏移值阈值Thr。实验采用控制变量法，依次确定各参数取值。

首先设R=4，Thr=0.7，从数据集图像中随机选取1 000个特征点，统计不同θ下改进算法分配单个特征点方向所需要的运行时间，给出SIFT算法所需要的时间以供参考，实验结果如图5所示。

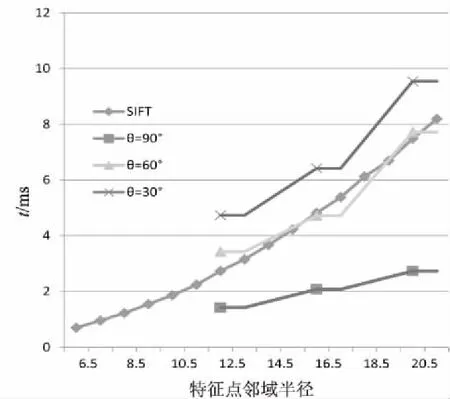
图5 运行时间

由于改进算法中，图像小块为对称结构的圆形区域，因此当R增加1个像素时，特征点邻域直径增加4个像素。实验结果表明，当θ为60°时，改进算法运行时间几乎等同于SIFT算法；当θ为90°时，改进算法运行时间为SIFT算法的36%～51%；而当θ为30°时，改进算法运行时间超出SIFT。因为当θ增大时，改进算法处理图像小块的数目急剧增加，Thr一定时，改进算法可忽略梯度计算过程的低偏移值区域，算法运行时间趋向于SIFT的运行时间，而计算各圆形图像小块的偏移值需要部分运行时间。综上所述，为保证算法性能，改进算法中取θ=90°。

接下来确定R的取值。从数据集图像中随机选取1 000个特征点，分别计算各特征点邻域图像小块的偏移值。在R取3、4、5时，由实验结果可知，当R取5时，由于圆形图像小块像素点较多，偏移均值太小且集中于0.4个像素以下；当R取4时，偏移均值总体偏小，质心趋向于特征点所在位置，此时偏移值均值为0.418 2个像素；当R取3时，偏移值均值为0.921 0个像素，偏移值分布较为理想，故改进算法中取R=3。

最后，Thr通过模拟环境下的实验选取，方法是：从boat图片集的img1图像中随机提取出500个特征点局部图像并旋转30°变换，从ubc、iguazu图片集的img1、img3图像中随机提取出500个一致匹配特征点对，以SIFT、SURF、CoM算法作为参考，计算各算法分配主方向的准确性。对SIFT算法与改进算法，当一个特征点具有多个主方向时，取误差较小的主方向为最终结果。期间做了大量的统计分析工作，由于篇幅有限，仅列出0.6～0.85之间取值的Thr，设置步长为0.5，纵轴取不同参数下角度偏差的平均值，实验结果如图6所示。

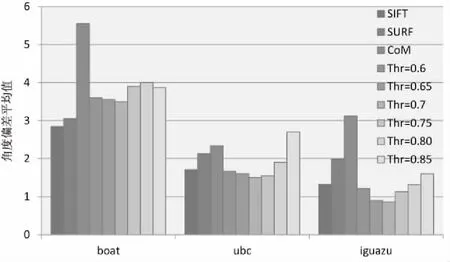
图6 模拟环境下各算法方向分配误差平均值

结果表明，当Thr=0.7时，改进算法稳定性较好。因此，在改进算法中，设置θ=90°，R=3，Thr=0.7。

3.2实验结果与分析

为进一步验证改进算法的有效性，以特征点匹配为应用背景，对比分析不同特征描述子的性能。实验中采用文献[14]的错误率1-precision和召回率recall曲线来描述算法性能。

错误率=

(5)

(6)

实验中选用指定阈值的特征性描述误差2-范数作为匹配策略，当误差值小于设定的阈值，则为匹配对，当匹配对所对应的特征点坐标误差小于2个像素，则该匹配对为正确匹配，否则为错误匹配。而后通过变化阈值来取得1-precision与recall曲线。

特征描述算法通常对图像的视角变化和噪声干扰较为敏感。当视角变化较大时，对算法性能是一种挑战。其中，视角变化图像采用graf、wall图片集，噪声干扰图像采用iguazu图片集。

分别对SIFT[15]、SURF[8]、HOI[10]及改进算法进行求解，由于实验集图片较多，在此仅分析wall数据集的P1-P3(img1与img3图像匹配，下同)特征点匹配结果与iguazu数据集P1-P2与P1-P3特征点匹配结果，并对各算法的1-precision与recall曲线作图，结果如图7所示。其他情况下各描述子的性能曲线排序规律与图7中一致，不再另作描述。

图7 特征点匹配实验结果

对于视角变化，改进算法的性能与SIFT、SURF相比略有不足，实验结果跟模拟实验结果保持一致，其原因可能在于当视角变化时，特征点局部区域背景发生较大改变，改进算法排除低偏移值区域反而使主方向分配受到一定干扰，导致准确率略有下降。

对于噪声干扰，改进算法表现出了较好的性能，在recall为0.85时，其准确率较SIFT算法提升了17%以上。其原因是改进算法通过排除低偏移区域，减少了噪声干扰对特征点主方向分配的影响。同时，实验结果也证实了特征点方向分配对特征描述具有显著影响，对带主方向分配的特征点描述算法，主方向分配的准确性将直接影响特征点匹配的准确性。

4 结束语

针对特征点方向分配算法的准确性易受噪声干扰的问题，提出一种改进的特征点方向分配算法。该算法采样特征点所在局部区域的圆形图像小块，并计算各圆形图像小块的质心偏移值，通过排除易受噪声干扰的低偏移值区域，减少噪声干扰对算法的影响。实验结果表明，该算法的时间复杂度低，对噪声干扰、光照、压缩变换等具有较强的鲁棒性。但当特征点局部发生较大的旋转、视角变化时，算法的性能略有下降，同时算法性能对参数取值较为敏感。因此，研究更加准确、通用的改进策略将是下一步努力的方向。

[1] 廖 斌.基于特征点的图像配准技术研究[D].长沙:国防科学技术大学,2008.

[2] 张琳波,肖柏华,王 枫,等.图像内容表示模型综述[J].计算机科学,2013,40(7):1-8.

[3] Yi K M,Verdie Y,Fua P,et al.Learning to assign orientations to feature points[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2016:107-116.

[4] Brown M,Szeliski R,Winder S.Multi-image matching using multi-scale oriented patches[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2005:510-517.

[5] Lowe D G. Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.

[6] Wang Y ,Shi M,You S,et al.DCT inspired feature transform for image retrieval and reconstruction[J].IEEE Transactions on Image Processing,2016,25(9):4406-4420.

[7] Taylor S,Drummond T.Binary histogrammed intensity patches for efficient and robust matching[J].International Journal of Computer Vision,2011,94(2):241-265.

[8] Bay H.SURF:speeded up robust features[J].Computer Vision & Image Understanding,2006,110(3):404-417.

[9] Alcantarilla P F,Bartoli A,Davison A J.KAZE features[C]//ECCV.[s.l.]:[s.n.],2012:214-227.

[10] Gauglitz S,Turk M,Höllerer T.Improving keypoint orientation assignment[C]//British machine vision conference.[s.l.]:[s.n.],2011.

[11] Kavukcuoglu K,Ranzato M A,Fergus R,et al.Learning invariant features through topographic filter maps[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2009:1605-1612.

[12] Roth S,Schmidt U.Learning rotation-aware features:from invariant priors to equivariant descriptors[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2012:2050-2057.

[13] Goh K M,Abu-Bakar S A R,Mokji M M,et al.Implementation and application of orientation correction on SIFT and SURF matching[J].International Journal of Advances in Soft Computing & Its Applications,2013,5(3):1-16.

[14] Mikolajczyk K,Schmid C.A performance evaluation of local descriptors[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2005,27(10):1615-1630.

[15] Vedaldi A,Fulkerson B.Vlfeat:an open and portable library of computer vision algorithms[C]//International conference on multimedia.[s.l.]:[s.n.],2010:1469-1472.

AnImprovedAlgorithmforAssigningOrientationstoFeaturePoints

JIA Qi，WANG Xiao-dan，ZHOU Lai-en，ZHAI Xi-yang

(Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China)

Existing feature point orientation assignment algorithm is easily disturbed by noise and its accuracy needs to be improved in illumination variation and affine transform.For this,an improved algorithm for assigning orientations of feature points is put forward based on SIFT.It fixes the interval in the range of 0～360 degrees with the feature points as the center,equidistant sampling of circular image blocks in several local area,calculating the offset value of the centroid for circular image blocks to center of that.According to the statistics theory and experimental verification,low offset value area is easily disturbed and has no effect on the determination of dominant orientation.Therefore it excludes the local area of low offset value,calculates the amplitude of the pixel gradient of the residual local area,and assigns the main direction to the feature points using the directional histogram.The results of experiments show that compared with SIFT algorithm,it has a relatively higher running speed and accuracy.In addition,during the feature point matching,its accuracy is basically identical with the existing algorithm in database with changeable viewpoint and improves by 17% in database with noise interference.

feature point;assigning orientations;SIFT;gradient

TP391.4

A

1673-629X(2017)10-0006-05

2016-11-30

2017-03-07 < class="emphasis_bold">网络出版时间

时间：2017-07-19

国家自然科学基金资助项目(61273275,60975026)

贾 琪(1993-)，男，硕士，研究方向为智能信息处理及模式识别；王晓丹，教授，博士生导师，研究方向为智能机器处理、机器学习。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170719.1113.092.html

10.3969/j.issn.1673-629X.2017.10.002