利用三角数列，巧数 三角形

匡家应

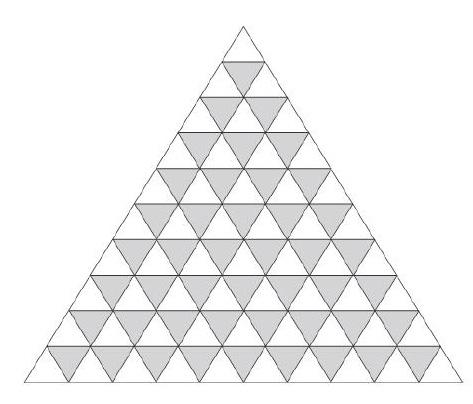
数图形是小学生数学学习的基本技能，也是学生发展逻辑思维、空间想象能力的重要途径，在人们的生产生活、建筑设计中也有着广泛应用。然而，数准图形又是数学教学中的难点，如下图所示，无论是学生还是老师，都很难在短时间内数出三角形的数量。

本人通过多年的教学实践，经过反复论证，借助三角数列轻松地解决了这一难题：

我们从“金字塔”的塔尖往下数：

第一层：1个三角形（①级）；

第二层：左边的3表示了3个①级小三角形，右边的1表示1个较大（由4个小三角形组成）的三角形（②级），共增加了4个三角形；

第三层：左边的5表示增加了5个①级小三角形，中间的2表示增加了2个②级的三角形，右边的1表示了1个（由9个小三角形组成）的三角形（③级），共增加了8个三角形；

第四层：左边的7表示增加了7个①级小三角形，中间的4表示增加了4个②级的三角形，2表示增加了2个③级的三角形，右边的1表示（由16个小三角形组成）的三角形（④级），共增加14了个三角形；

第五层：左边的9表示增加了9个①级小三角形，中间的6表示增加了6个②级的三角形，3表示增加了3个③级的三角形，2表示增加了2个（④级的三角形，右边的1表示（由25个小三角形组成）的三角形（⑤级），共增加21了个三角形；

第六层：左边的11表示增加了11个①级小三角形，中间的8表示增加了8个②级的三角形，5表示增加了5个③级的三角形，3表示增加了3个④级的三角形，2表示增加了2个⑤级的三角形，右边的1表示（由36个小三角形组成）的三角形（⑥级），共增加30了个三角形；

第七層：左边的13表示增加了13个①级小三角形，中间的10表示增加了10个②级的三角形，7表示增加了7个③级的三角形，4表示增加了4个④级的三角形，3表示增加了3个⑤级的三角形，2表示增加了2个⑥级的三角形，右边的1表示（由49个小三角形组成）的三角形（⑦级），共增加40了个三角形；

第八层：左边的15表示增加了15个①级小三角形，中间的12表示增加了12个②级的三角形，9表示增加了9个③级的三角形，6表示增加了6个④级的三角形，4表示增加了4个⑤级的三角形，3表示增加了3个⑥级的三角形，2表示增加了2个⑦级的三角形，右边的1表示（由64个小三角形组成）的三角形（⑧级），共增加52了个三角形；

第九层：左边的17表示增加了17个①级小三角形，中间的14表示增加了14个②级的三角形，11表示增加了11个③级的三角形，8表示增加了8个④级的三角形，5表示增加了5个⑤级的三角形，4表示增加了4个⑥级的三角形， 3表示增加了3个⑦级的三角形， 2表示增加了2个⑧ 级的三角形，右边的1表示（由81个小三角形组成）的三角形（ ⑨级），共增加65 了个三角形；

第十层：左边的19 表示增加了19个①级小三角形，中间的16表示增加了16个②级的三角形，13表示增加了13个③级的三角形，10表示增加了10个④级的三角形，7表示增加了7个⑤级的三角形，5表示增加了5 个⑥级的三角形，4 表示增加了4 个⑦级的三角形，3表示增加了3个⑧ 级的三角形，2表示增加了2个⑨级的三角形，右边的1表示（由100个小三角形组成）的三角形（⑩级），共增加80 了个三角形；

往后以此类推，故此图共有：

1 + 4 +8 +14 + 21 + 30 + 40 + 52 + 65 + 80 = 315（个）三角形。

通过三角数列的应用，大大降低了学生数三角形数量的难度，提高了学生的逻辑思维能力，还能培养学生学习数列的兴趣。

其实，学习数学的乐趣有很多很多，只要我们善于 观察、善于总结、善于研究、善于实践，做个数学实践的有心人，就会找到一些简单有效的办法，也就能培养师生善学、乐学数学的习惯，就能不断提高数学教育教学质量，不断提高师生的数学素养。