例析辅助线在物理解题中的作用
张文华


摘要:本文通过几个典型例题来说明辅助线在解答物理习题中可以起到创立物理情境、构建物理模型、揭示隐含条件、简化运算过程等诸多作用,为化解高中物理中的一些疑难问题提供了一个重要的方法。
关键词:辅助线 物理 习题 作用
我们都知道,辅助线在求解几何题中起到举足轻重的作用,很多非常棘手的几何题,通过添加辅助线,将题设条件与所要求证的结果有效地连接起来,由原来的百思不得其解变得茅塞顿开,让感到无从下手的难题得以迎刃而解,其精妙简约之处,无不令人拍案叫绝,叹为观止。如果我们将几何中作辅助线的方法迁移到求解物理习题中来,通过辅助线来转化物理情景,构建物理模型,揭示隐含条件,寻找解题方法,简化运算过程,同样也将给物理习题的解答带来非同凡想的效果。下面我就通过几个例子来浅要说明辅助线在物理解题中的作用。
(1)如图所示,曲线1、3是卫星绕地球做圆周运动的轨道,曲线2 是卫星绕地球做椭圆运动的轨道,曲线3与曲线2相切于B点,O点为地球球心,AB为椭圆的长轴,三轨道和地心都在同一平面上。设卫星在圆轨道1、3运动的速率分别为V1、V3,在椭圆轨道上A点B点的速率分别为VA、VB,试比较这四个速率的大小。
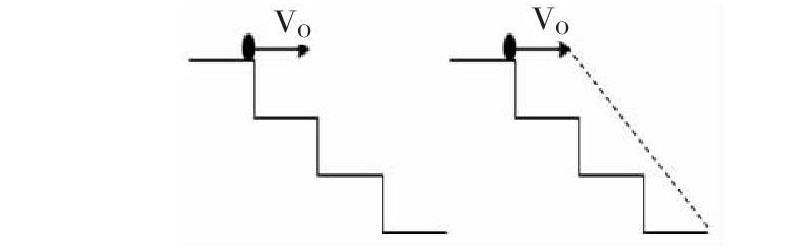
(2)如图所示,一小球从楼梯第一级台阶边缘以水平速度V0=2m/S滚下,所有楼梯的台阶都是高h=0.2m、宽L=0.25m,试问小球首先撞在第几级台阶上?(g取10m/s2)
解析:小球从第一级台阶边缘滚下后,在空中做平抛运动。由于台阶有突出的棱角,小球运动时会与其发生碰撞,因而要直接求出小球下落的时间,并由此确定撞到的台阶级数是比较困难的。如果把台阶边缘上的点用一直线连接起来,这样就可以把小球看作是从斜面上某一点水平抛出又落在斜面上另一点的平抛运动。设小球水平抛出后经时间t碰到“斜面”上,在这段时间内的水平位移x=V0t(1);竖直位移y= gt2(2);X/y=L/h(3);由(1)(2)(3)得x=0.65m,∵0.5m (3)如图所示,在半径为R的圆形区域内有匀强磁场,方向与圆面垂直,磁感应强度B均匀变化且变化率ΔB/Δt=k,在该区域内的图示位置放一根长为R的导体ab,求导体ab两端的电势差。 解析:这道题初看起来,只有一根导线在变化的磁场中,没有形成闭合回路,似乎缺乏条件,不能够求出导体ab两端的电势差。但如果根椐对称性,在圆形区域的边界内添加五条与ab完全相同的直导线作为辅助线(如图中的虚线)(这样可以使每根导线两端的电势差与ab两端的电势差相同),使它们一起构成一个内接正六边形,并形成一个闭合回路,这一棘手问题就可以巧妙化解。 (4)如图所示,O是等边三角形ABC的中心,D是三角形中的任意点,如果作矢量 、 、 分别表示三个力,三个力的方向如图中箭头所示,則这三个力的合力大小用 的长度表示为( ) 解析:由于D点是三角形中的任意一点,因而DA、DB、DC表示的三个力大小、每两个力间的夹角都无法确定,所以用常规方法求这三力的合力就显得非常困难。如果采用作辅助线的方法,连接AO、BO、CO,将这三条有向线段看作三个共点力,这三个力大小相等,且三力互成1200,因而这三条辅助线所表示的三个力的合力为零,添加这三个力不影响所求问题的答案。然后借助这三条辅助线所表示的三个力,利用三角形定则分别求出 与 的合力为 , 与 的合力为 , 与 的合力为 ,所以 、 、 所表示的三个力的合力大小等于3DO,方向为由D指向O。 添加辅助线的目的是使隐蔽的条件得以显现,再通过搭桥引线,来衔接已知量与未知量间的关系,从而寻找到正确的解题方法。但辅助线的作法是千变万化的,对不同的问题需要添加不同的辅助线,即使同一问题,由于分析方法的不同或思考问题的角度不同,所作的辅助线也可能不尽相同。究竟在哪一位置需要添加辅助线,添加什么形状的辅助线,所作的辅助线对解题能起到什么的有效作用,这些都必须认真分析,深入思考。对一些物理习题来说,所作的辅助线往往决定着解题的成败,而找準问题的切入点又成为正确作出辅助线的关键所在。因此,物理教师在教学中要重视对学生进行发散思维的训练,引导学生对同一问题能够从多角度、多方面、多层次进行认真细致的思考,使思维既有深度,又有广度,更有灵活性和开放性。在遇到一些相关问题时,能充分发挥辅助线在物理解题中的独特作用,巧作辅助线,妙解物理题。 参考文献: (1)《浅谈辅助线在解决物理问题中的作用》,马卉,蓝坤彦,物理教师,2014年第6期P85-86 (2)《重视辅助线在解决物理问题中的作用》,郭裕娟,中学物理,2010年第21期 (3)《“巧”作辅助线 解决物理“难”题》,李庆国,中学物理·高中版,2014年第2期P62 (4)《巧用辅助线解习题》,韩治忠,中学物理教学参考,2007年第8期

