一种结合卷积编码的新型空移键控系统

郭鹏程，周长征，郑家祥

(中国洛阳电子装备试验中心，河南 洛阳 471000)

一种结合卷积编码的新型空移键控系统

郭鹏程，周长征，郑家祥

(中国洛阳电子装备试验中心，河南 洛阳 471000)

提出了一种与卷积编码结合的新型空移键控系统，并给出了三种卷积编码结构。首先，重点介绍了系统的传输模型以及卷积编码构造；其次，分析了系统接收端天线检测所采用的译码算法，并对接收算法复杂度作了比较；最后，在莱斯衰落信道下对该方案的传输性能进行了仿真分析，比较了不同卷积编码构造下的方案与传统的空移键控技术的优劣势。结果表明：该方案可以很好地提高系统的抗信道衰落性能。

卷积编码；莱斯衰落信道；空移键控

0 引言

MIMO技术发展迅速，其通过并行的子信道来实现空间复用，从而能显著提高系统传输速率与频谱利用率，如贝尔实验室的垂直分层空时编码技术(V-BLAST)[1-2]。MIMO技术通过增加系统复杂度和费用为代价换取更好的误码率性能和数据传输速率。但在实际应用中会存在一些问题，如信道间干扰以及多天线间的同步问题。

由R.Mesleh和H.Haas提出的空间调制技术(Spatial Modulation，SM)[3-5]一定程度上克服了这些问题，其核心思想是：在所有的发送天线中每时刻只有一根天线处于激活状态，被选择用来发送信息，其余天线处于静默状态。天线序号携带部分发送信息，其余信息通过常规调制来实现，而接收端通过天线序号的估计和发送符号的解调来恢复信息。这样，空间调制[6]可以有效避免信道间干扰和多天线发射的同步性问题，同时打破了传统MIMO中对收发天线数目的限制。

J.Jeganathan和A.Ghrayeb等人在空间调制的基础上提出了空移键控技术(Space Shift Keying，SSK)[7]，仅通过激活发送端天线序号来实现信息调制，与空间调制相比取消了数字调制解调环节，通过与单天线调制、V-BLAST以及SM的性能比较，在相同的频谱利用率的情况下，SSK具有与SM相似的性能，并优于传统的单天线调制，考虑到其低复杂度，一定程度上可以说明SSK的优越性。文献[8]在SSK基础上引入了空间分集技术，提出了广义空移键控调制(Generalized Space Shift Keying，GSSK)的概念，通过从多根发送天线中选择天线组合的形式来调制信号，可以以较小的天线成本满足系统性能的要求，更充分地利用了空间资源，提高了频谱利用率。

为了提高SSK的传输性能，本文提出了将卷积编码与SSK结合的天线映射方案，为方便描述，将其称为CSSK，并通过仿真对比分析了两种调制模式在莱斯信道下的性能。

1 CSSK原理

1.1CSSK传输模型

空移键控(Space Shift Keying，SSK)调制的基本原理是：发送端信息全部映射在天线序列上，每时刻只有一根天线处于激活状态，发送信息通过选择不同的天线选择来表示，发送脉冲符号并未调制任何信息，仅仅用来表示发送天线的工作状态。而其余天线处于静默状态，天线本身的位置信息携带了发送信息。在接收端，只需检测发射天线位置序号即可，然后通过解映射规则恢复信息序列。在空移键控技术中，空移键控没有数据调制，在发送装置上更加简单，如减少了功放、射频滤波器、数模转换等调制装置，因此具有更低的系统复杂度。

CSSK传输模型如图1所示，输入数据首先进行卷积编码，编码输出后，经过一定的天线调制规则选择发送天线，此时发送符号与SSK一致，可表达为矢量形式:x“1”所处的位置代表被激活的天线位置，“0”表示天线静默。莱斯信道为矩阵H，H是一个Nr×Nt复数矩阵，对应莱斯因子k，矩阵中元素代表相应发送天线到接收天线的信道增益。

图1 CSSK传输模型

发送数据经过卷积编码后进行天线选择，此时须满足一定的天线调制规则，由于系统发送功率一定，即E[XHX]=1，举例说明，当发送天线数目Nt=8时，SSK映射如表1所示。

表1 SSK映射

表1表示一种Nt=8的天线调制规则，每时刻从8根天线中选择一根发送天线，表示3 bit发送信息。M维SSK映射可以表示的有效信息位为log2(M)，此时发送天线数Nt须满足Nt=M。

在莱斯信道条件下，接收信号可以表示为[7]：

(1)

其中，ρ为每根接收天线的平均信噪比(SNR)；h表示信道矩阵H第列，说明信道H中只有第列处于激活状态；η为Nr维噪声信号，满足复高斯分布CN(0,1)。经过莱斯信道H后，接收端首先进行天线检测，解调信息后再进行Viterbi反馈译码，最后恢复发送信息。

1.2卷积编码构造

CSSK中采用的卷积编码构造如图2所示。

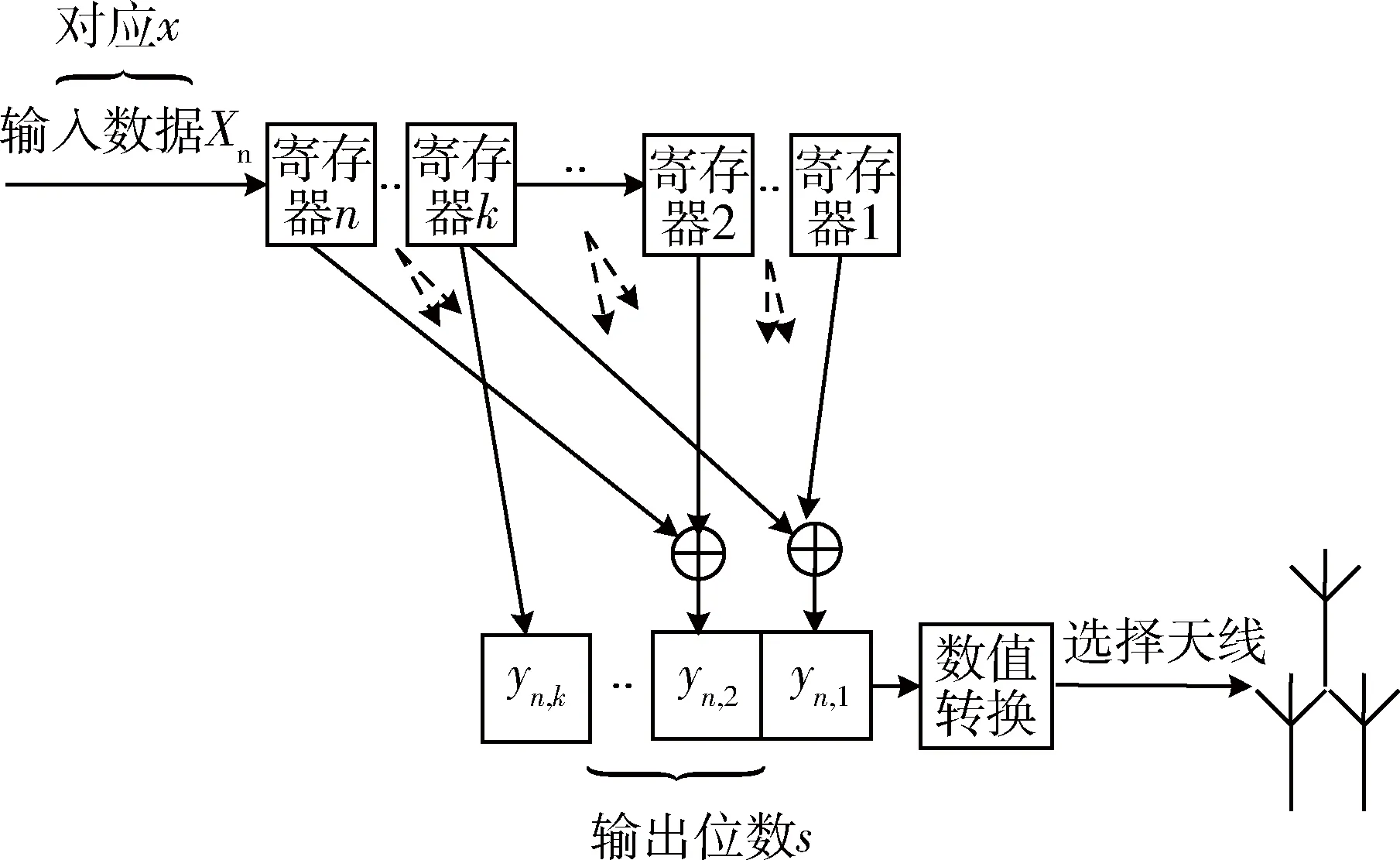
图2 卷积编码构造

图中x表示每一次天线切换所传输的信息比特个数，s表示输出位数。输入数据Xn进入卷积构造进行卷积编码，通过与寄存器中的数据运算，输出信息通过数值转换后选择发送天线序号，而且输出位数s对应发送天线数目Nt，对应关系为Nt=2s。因此，卷积构造主要由两个要素决定，即x和s，x决定信息卷积输入，s决定卷积输出，两者改变任意一个意味着卷积结构的改变。

输入数据与寄存器之间的卷积关系具有一定灵活性，而探索一种有效的卷积结构对系统性能至关重要。本文列举了3种卷积结构，分别为构造1：x=1，s=3，发送天线Nt=8；构造2：x=1，s=4，发送天线Nt=16；构造3：x=2，s=3，发送天线Nt=8。构造1如图3所示。

图3 Nt=8、x=1的卷积编码构造

在图3中，输入数据Xn进入卷积编码器，通过与两个寄存器中的数据运算得到三位输出值(yn,3,yn,2,yn,1)，通过转换选择相应的发送天线。

构造2对输出位数进行了扩展，即发送天线数目由8增加到16，输入数据与寄存器之间的卷积关系不变，如图4所示。

当改变输入数据位数，每次天线跳变由传输1 bit信息变为2 bit，同时发送天线数目不变时，即为构造3，如图5所示。当x=2时，卷积函数的构造会有更多选择的空间，复杂度也会大大增加，同时不同的卷积构造形式对系统性能影响较大，图5采取一种两输入三输出的构造形式。

图4 Nt=16、x=1的卷积编码构造

图5 Nt=8、x=2的卷积编码构造

2 接收算法

(2)

(3)

得到天线位置序号后，对天线序号进行解映射，恢复相应的信息比特，这种解映射属于简单的十进制转二进制过程，因此，天线检测与解映射可以看作一个整体。可以将这个整体作为天线位置进行路径搜索，进行Viterbi反馈译码，对检测错误的天线进行纠错，从而恢复信息序列。

3 复杂度分析

从复数乘法的角度分析，CSSK与SSK有着相同的运算量[3]，即：

δCSSK=δSSK=NrM

(4)

M表示整个星座调制大小，相当于发送天线数目，即M=Nt；从复数加法的角度考虑，对SSK而言，运算量为：

ζSSK=2NrM-M

(5)

再来分析CSSK的复数加法运算量，接收端在进行天线检测后，对解映射信息进行Viterbi反馈译码，从而恢复信息序列。以图3中卷积编码函数构造为例，信息状态有4个，在译码过程中，取译码深度为3，可以保证所有状态都能汇合，状态转移关系如图6所示。

图6 卷积函数状态转移图

其加法运算量可以表示为:

ζCSSK=2NrM-M+2L

(6)

L表示状态个数，此外，CSSK在每时刻会有L次比较运算。因此，CSSK相比于SSK会有更大的算法复杂度。

4 CSSK性能仿真分析

仿真条件1：莱斯衰落信道，莱斯因子k=1，仿真点数num=200 000，接收天线数目Nr=8，发送天线数目分别为Nt=8和Nt=16，卷积编码构造1与构造2下的CSSK与SSK性能比较。

仿真结果如图7所示，可以看出：在莱斯衰落信道中，当占用相同的天线资源时，构造1下的CSSK传输性能优于SSK，在BER为10-3时，CSSK优于SSK约2 dB；而构造2下的CSSK传输性能优于SSK约3 dB，但代价是每次天线切换传输信息比特数的下降。同时，对相同接收天线数目条件下，构造1条件下SSK与CSSK均优于构造2，说明发送与接收天线数目的相对数目对系统传输性能影响较大。

图7 莱斯信道下CSSK、SSK性能比较

仿真条件2：莱斯衰落信道，莱斯因子k～(0～3)，仿真点数num=200 000，收发天线数目Nr=8和Nt=8， 卷积编码构造3下的CSSK与SSK性能比较。

仿真结果如图8所示，可以看出：在相同的收发天线数目下，随着莱斯因子的增大，SSK与CSSK的传输性能都在逐渐下降，由k=0到k=1时，性能下降最明显，在BER为10-3时，SSK与CSSK性能均下降约3 dB左右,而从k=1到k=2,k=2到k=3时，SSK与CSSK性能均下降约1 dB左右。CSSK与SSK相比，当占用相同的天线资源时，在相同k值情况下，CSSK性能均要优于SSK，在BER为10-3、k=1时，CSSK性能优于SSK约1.5 dB左右。

图8 不同莱斯因子条件下CSSK、SSK性能比较

CSSK经过卷积编码及Viterbi译码，对系统的传输性能有了较大的提升，但也存在一定的限制。例如，发送端天线的数目对应信息卷积结构输出，而每次切换所传输比特数对应卷积结构输入，而两者任一改变意味着卷积结构的改变。此外，当发送天线为Nt=8，每次天线切换时，SSK能传输3 bit信息，而构造3下CSSK只能传输2 bit信息，这也是CSSK提升信道抗衰落性能所付出的代价。

CSSK通过卷积构造产生的天线序列随机性有了较大改观，这种卷积构造除了改善系统传输性能外，也使得天线序号由直接映射转变为非线性运算，获得了较好的随机性，从而增加了系统的抗破译与抗截获性能[10]。

5 结论

本文提出了一种将卷积编码与SSK结合的新型空移

键控技术(CSSK)，对CSSK的传输模型以及卷积编码构造进行了详细介绍，并对接收端天线检测与复杂度进行了深入分析。通过在莱斯信道下对SSK与CSSK的性能仿真比较，证明了CSSK相比于SSK提高了系统的抗信道衰落性能，代价是每次天线切换传输比特数的下降，但这一点也可以通过改进卷积编码构造进行完善。此外，CSSK提升了发送端天线序列的随机性，这样可以额外增加系统的抗截获性能。下一步可以考虑将卷积编码构造与GSSK相结合，这样不仅能节省天线资源，提高传输效率，其组合样式也会大大增加。

[1] WOLNIANSKY P W, FOSCHINI G J, GOLDEN G D, et al. V-BLAST: an architecture for realizing very high data rates over the rich-scattering wireless channel[C]. International Symposium on Signals, Systems, and Electronics (ISSSE′98), 1998: 295-300.

[2] GOLDSMITH A, JAFAR S, JINDAL N, et al. Capacity limits of MIMO channels[J].IEEE Journal on Selected Areas in Communications(JSAC), 2003, 21(5): 684-702.

[3] ALSHAMALI A, QUZA B. Performance of spatial modulation in correlated and uncorrelated nakagami fading channel[J]. Journal of Communications, 2009, 4(3): 170-174.

[4] MESLEH R, HAAS H, AHN C W, et al. Spatial modulation-OFDM[C].11th International OFDM-Workshop 2006(InOWo′06), 2006: 288-292.

[5] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L. Spatial modulation: optimal detection and performance analysis[J]. IEEE Communication Letters, 2008，12(8): 545-547.

[6] MESLEH R, HAAS H, SINANOVIC S, et al. Spatial modulation[J]. IEEE Transonetions on Vehicular Technology, 2008, 57(4): 2228-2241.

[7] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L, et al. Space shift keying modulation for MIMO channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(7): 3692-3703.

[8] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L. Generalized space shift keying modulation for MIMO channels[C]. IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications, 2008: 15-18.

[9] 樊昌信, 曹丽娜. 通信原理(第6版)[M]. 北京: 国防工业出版社, 2015.

[10] 姚富强. 通信抗干扰工程与实践(第2版)[M]. 北京: 电子工业出版社, 2012.

A new type of space shift keying modulation combined with convolutional coding

Guo Pengcheng, Zhou Changzheng, Zheng Jiaxiang

(Luoyang Electronic Equipment Test Center of China, Luoyang 471000, China)

In this paper, a new space shift keying modulation scheme combined with convolutional coding is proposed, and three convolutional coding structures are given. Firstly, the transmission model and the convolutional coding structure of the system are introduced. Secondly, the decoding algorithm of antenna detection used in the receiver is analyzed, and the complexity of the receiving algorithm is compared. Finally, the transmission performance of the scheme is simulated and analyzed in the Rician fading channel, and the advantages and disadvantages of the scheme under different convolution coding structures and traditional space shift keying modulation are compared. The results show that the proposed scheme can prove the anti-channel fading performance of the system.

convolutional coding; Rician fading channel; space shift keying

TP918

A

10.19358/j.issn.1674- 7720.2017.19.018

郭鹏程，周长征，郑家祥.一种结合卷积编码的新型空移键控系统[J].微型机与应用，2017,36(19)：62-65,69.

2017-05-12)

郭鹏程(1991-)，通信作者，男，硕士，研究实习员，主要研究方向：通信抗干扰与编码调制。E-mail: kaka_pc@163.com。