基于矩阵填充的SVD协同过滤算法研究*

王祥德，雷玉霞，闫昱姝

(曲阜师范大学 信息科学与工程学院，山东 日照 276800)

基于矩阵填充的SVD协同过滤算法研究*

王祥德，雷玉霞，闫昱姝

(曲阜师范大学 信息科学与工程学院，山东 日照 276800)

对协同过滤推荐算法中数据稀疏问题，提出矩阵填充策略，分析矩阵填充技术的优劣，选择非精确拉格朗日乘子法对稀疏矩阵填充，对填充的矩阵使用SVD协同过滤算法进行推荐，对推荐结果分别用平均绝对误差、均方根误差和标准平均绝对误差方法进行评估。实验结果表明，运用矩阵填充的推荐算法提高了推荐的质量。

协同过滤；SVD协同过滤；矩阵填充

0 引言

随着互联网规模的扩大，数据呈现爆炸式增长，传统的信息搜索方法搜索到的符合要求的结果变得越来越多，这就增加了用户获取有价值信息的难度。弥补信息检索存在的这些缺陷，个性化推荐系统应运而生。

个性化推荐系统从2000年开始得到广泛应用，明尼苏达大学的Sarwar教授的文章[1]详细地介绍了基于项目的协同过滤算法，是学者们研究协同过滤推荐算法常引用的文章。2004年以后，推荐算法开始融合基于内容和基于模型的推荐，之后Sarwar等人[2]将SVD引入到协同过滤推荐算法中。在推荐数据中，有些信息是涉及用户隐私的数据，这一部分数据有可能影响推荐的准确性。Polat等人[3]给出了带有隐私的SVD协同过滤算法，优化了这一问题。针对现有协同过滤算法具有的可扩展性较低、数据稀疏和计算量较大的缺点，刘洋等人[4]提出一种基于SVD矩阵分解技术和RkNN算法的协同过滤推荐算法。陈清浩等人[5]提出了梯度下降法改进的SVD协同过滤算法。本文在SVD协同过滤算法的基础上，将矩阵填充技术引入其算法中。

1 相关定义及推荐算法

1.1协同过滤算法

协同过滤推荐算法[6-8]包括基于内存的协同过滤算法和基于模型的协同过滤算法，常用的推荐算法有基于用户的协同过滤算法(UBCF)、基于项目的协同过滤算法(IBCF)[9]、基于SVD的协同过滤算法。协同过滤推荐算法的基本原理是通过“用户-项目”评分矩阵计算相似度，用计算出来的相似度对目标用户做推荐。用户对项目的评分矩阵可以表示成m×n维的矩阵，其中，m和n分别是推荐系统中用户和项目的数目，每一个元素ru,i表示用户u对项目i的评分。

1.2相似度及预测评分

相似度是指两个用户对同一个项目的喜好程度或者两个项目被同一个用户喜好的相似程度。常用的相似度模型有余弦相似性、修正的余弦相似性、Pearson相关相似性和受约束的Pearson相关相似性[10]等。Pearson相关相似性在同等情况下具有更加有效的性能，计算用户相似度的Pearson相关相似性表达式为：

(1)

其中Iuv表示用户u、v共同评分的项目集合。计算项目的相似度的Pearson相关相似性表达式为:

(2)

其中Uij表示对项目i、j共同评分的用户集合。

预测函数有均值函数、权重函数和改进型权重函数。最常用的改进型权重函数表达式如下：

(3)

1.3SVD协同过滤算法

奇异值分解(Singular Value Decomposition，SVD)[11]是线性代数中的矩阵分解方法，可以将高维矩阵降维成低维矩阵。Sarwar等人将SVD引入到协同过滤推荐算法中，用SVD方法对评分矩阵进行分解，并用评分矩阵的奇异值提取特征，用这些特征进行推荐。

SVD算法原理:

(4)

它表示前k个奇异值的平方和与所有奇异值平方和的比值，一般地，前1%左右的奇异值就能表示99%原矩阵的信息，所以在此取α值为99%，以此求得k的值。从Σ中取得前k大的奇异值组成新的对角阵Σk，从U、V中选取前k个左右奇异向量，组成新的Uk和Vk，降维后的评分矩阵为：

其中k远小于m,n。

1.4现有算法的不足

数据稀疏是当前推荐系统面临的最主要的问题，数据稀疏也导致了推荐精确度的降低。目前网络系统中各种数据激增，然而用户对这些项目的评分却不足，这使得评分矩阵缺失严重，用户项目之间的相似度计算愈加困难，以Netflix Prize 为例，其数据缺失达98%以上。因此，本文提出了一种解决数据稀疏问题的算法。

2 矩阵填充算法

矩阵填充(Matrix Completion,MC)可以看作特殊的矩阵恢复问题，是Candes等人[13]在2009年提出的方法，主要研究数据不完整情况下缺失数据的填充问题。矩阵填充的前提是矩阵的低秩性，推荐系统中，用户的评分矩阵是低秩的，可以用矩阵填充的办法解决数据稀疏问题。

在比较矩阵填充技术的优势上，选择Lin等人[14]提出的非精确拉格朗日乘子法进行填充，矩阵填充可描述为以下优化问题：

s.tA+E=D

πΩ(E)=0

(5)

在πΩ(E)=0的约束下，更新E取得优化算式L的最小值。

填充完成后，用户对项目的评分为：

3 基于矩阵填充的SVD协同过滤算法(MCSVD)

3.1算法的实现

输入：评分数据集

输出：目标用户u对未评分项目i的评分预测

矩阵填充的SVD协同过滤算法

1. 由矩阵填充算法将矩阵R填充为R1

2.U,Σ,V=linalg.svd(R1)

3. 由式(4)≥99%计算k的值

4.Σk=diag(Σ)[:k,:k]

5.Uk=U[:,:k],Vk=V[:,:k]

6.Ur=Uk*sqrt(Σk),Vr=sqrt(Σk)Vk.T

7.Rui=Ur(u)*Vr(i)

3.2预测准确度

使用预测准确度评估算法的优越性，预测准确度是指推荐算法的预测评分与用户的实际评分是否接近，在推荐系统中，预测准确度是很重要的参数，例如，推荐系统给用户的预测评分数和用户实际的评分数非常接近，可以说系统成功地完成了预测用户的兴趣。

常用的预测评分准确度标准有：平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Squared Error, RMSE)。

平均绝对误差。MAE衡量的是所有用户准确度的平均，在推荐系统评估度量中广泛应用，定义如下：

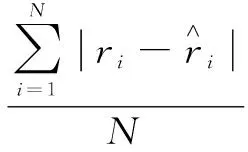
(6)

均方根误差。RMSE在求和之前先让预测评分与实际评分的误差进行评分，该标准加大了对不准确评分预测的惩罚力度，对系统评分更加苛刻，因此评分误差越大，对RMSE值影响越大，定义如下：

(7)

4 实验分析

4.1实验数据集

在个性化推荐算法研究领域，最常用的数据集有Movielens电影评分数据集、Libimseti网上约会评分数据集、Book-Crossing书籍评分数据集和Jester笑话评分数据集。这里使用Movielens数据集，此数据集是由美国明尼苏达大学Grouplens项目从Movielens站点整理而来，并广泛应用于个性化推荐算法研究中，数据集中每个用户至少对20部电影进行评分，评分的范围从1～5， 评分值越高表示越满意。

4.2实验设计和结果分析

试验中，将数据分为训练集和测试集，在第一个试验中，选取80%的数据作为训练集，分别对原始评分矩阵和填充的矩阵在训练集上使用SVD协同过滤算法进行训练，将训练结果在测试集上进行测试，对得出的结果使用不同的准确度评估方法进行评估，实验结果如下表1所示。数据显示，矩阵填充之后精确度提高。

表1 实验结果

第二个实验中,对给出的given(预测项目数)值，进行不同方法的多组比较，实验结果如图1所示。实验数据表明，在不同方法中，基于矩阵填充的奇异值分解方法具有较好的推荐效果，同时given值对推荐系统影响很大(取值范围为0～20)，given值越大，推荐准确度越高。

图1 不同预测项目数下精确度曲线

第三个实验中，将数据集中不同的用户数作为训练集，分别在不同的推荐方法中训练预测，得到的实验结果如图2所示。实验结果表明，基于矩阵填充的奇异值分解方法精确度曲线优于其他结果，同时，在训练用户大于等于400时，曲线趋于平稳，这也说明在一定的训练/测试比下，训练/测试比对评分准确度影响不大，并不是训练集比重越大评分准确度越大，因此在实际过程中可适当降低训练集的比例，减少建立模型所需时间。

图2 不同用户数下精确度曲线

5 结束语

本文分析了协同过滤算法及其存在的一些问题，并提出了基于矩阵填充的SVD协同过滤算法，首先采用矩阵填充技术对评分稀疏矩阵进行填充，解决了数据稀疏问题，然后将填充的评分矩阵应用到SVD协同过滤算法中，计算预测结果的评分准确度。实验结果表明，基于矩阵填充的SVD协同过滤算法在评分准确度上有所提高，但是填充的矩阵由于数据量过大，给内存和计算都带来挑战，这是下一步将要解决的问题。

[1] SARWAR B, KARYPIS G J. Item-based collaborative filtering recommendation algorithms[C]. Proceedings of the 10th International Conference on World Wide Web, ACM, 2001: 285-295.

[2] SARWAR B, KARYPIS G, KONSTAN J, et al. Application of dimensionality reduction in recommender system-a case study[R]. Minnesota Univ Minneapolis Dept of Computer Science, 2000.

[3] POLAT H, DU W. SVD-based collaborative filtering with privacy[C]. Proceedings of the 2005 ACM symposium on Applied computing. ACM, 2005: 791-795.

[4] 刘洋. 基于 SVD 矩阵分解技术和 RkNN 算法的协同过滤推荐算法[J]. 湖南工程学院学报 (自然科学版), 2015,25(1): 44-47.

[5] 陈清浩. 基于SVD的协同过滤推荐算法研究[D]. 成都：西南交通大学, 2015.

[6] BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[C]. Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence, 1998: 43-52.

[7] LIU Q, CHEN T, CAI J, et al. Enlister: baidu’s recommender systems for the biggest Chinese Q&A website[C]. Proceedings of the ACM Conference on Recommender Systems, 2012: 285-288.

[8] Zheng Nan, Li Qiudan, Liao Shengcai, et al. Which photo groups should I choose? a comparative study of recommendation algorithms in flickr[J]. Joumal of Information Science, 2010, 36(6): 732-750.

[9] 邓爱林, 朱扬勇, 施伯乐. 基于项目评分预测的协同过滤推荐算法[J]. 软件学报, 2003, 14(9): 1621-1628.

[10] 徐翔, 王煦法. 协同过滤算法中的相似度优化方法[J]. 计算机工程, 2010, 36(6): 52-54.

[11] WALL M E, RECHTSTEINER A, ROCHA L M. Singular value decomposition and principal component analysis[M]. A Practical Approach to Microarray Data Analysis. Springer US, 2003: 91-109.

[12] 陈峰峰. 奇异值阈值算法在Netflix问题中的应用研究[D]. 北京: 清华大学, 2011.

[14] CHEN M, LIN Z, MA Y, et al. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. Eprint Arxiv, 2010.

Research on singular value decomposition collaborative filtering algorithm based on matrix completion

Wang Xiangde, Lei Yuxia, Yan Yushu

(College of Information Science and Engineering, Qufu Normal University, Rizhao 276800, China)

A matrix completion scenario was proposed to solve the problem of matrix sparsity in collaborative filtering recommendation. After analyzing various technologies of matrix completion, the inexact augmented Lagrange multiplier was selected to recover the matrix. Using singular value decomposition collaborative filtering algorithm on the recovered matrix. Evaluating recommended data utility the measure of Mean Absolute Error, Root Mean Squared Error. The experimental results show that the accuracy is higher when using the recovered matrix.

filtering recommendation; SVD filtering recommendation; matrix completion

TP301.6

A

10.19358/j.issn.1674- 7720.2017.19.016

王祥德，雷玉霞，闫昱姝.基于矩阵填充的SVD协同过滤算法研究[J].微型机与应用，2017,36(19)：55-57,61.

国家自然科学基金项目(61572284,61502272)；山东省中青年优秀科学家基金项目(BS2014DX004)

2017-03-14)

王祥德(1989-)，通信作者，男，硕士研究生，主要研究方向：数据挖掘，大数据分析和分布式计算。E-mail:386345486@qq.com。雷玉霞(1976-)，男，博士，副教授，主要研究方向：知识表示与获取，知识本体。闫昱姝(1991-)，女，硕士研究生，主要研究方向：数据挖掘。