一类非线性最优控制问题的间断有限元方法

杨继明，朱先睿

(湖南工程学院 理学院，湘潭 411104)

一类非线性最优控制问题的间断有限元方法

杨继明，朱先睿

(湖南工程学院 理学院，湘潭 411104)

对于一类非线性最优控制问题，采用间断有限元方法进行离散求解.数值实验表明，间断有限元方法能有效求解所研究的最优控制问题.

最优控制；间断有限元方法；非线性

0 引言

偏微分方程最优控制在科学和工程领域中发挥着重要的作用，这类问题数值方法的研究受到许多学者的关注.

严宁宁和刘文斌等采用有限元法对椭圆最优控制问题进行了研究[1].陈艳萍教授等在最优控制问题的混合有限元方法上做了大量工作[2-3].马和平教授等人研究了最优控制问题的Chebyshev-Legendre配置法[4].陈艳萍教授、周建伟教授在文献研究了最优控制问题的谱方法[5-7].Meyer等研究了线性二次椭圆最优控制问题有限元法的先验误差和超收敛性质[8-9].Merino研究了Burgers方程最优控制问题的有限元方法[10].

间断有限元方法是利用完全间断的分片多项式空间作为近似解和试验函数空间的一种非协调有限元方法.它已经在许多含有激波、接触断面、大梯度、大变形等间断问题上显示出强大的功效[11-14].但关于最优控制问题间断有限元方法的研究工作很少.

本文采用间断有限元方法求解一类非线性最优控制问题.

1 问题描述

设Ω和ΩU是有界凸多边形区域，其边界分别为∂Ω和∂ΩU.定义相应的控制集：

Uad={v∈L2(ΩU),v≥0},U=L2(ΩU).

考虑一类非线性最优控制问题：

s.t.-Δy+φ(y)=f+Bu,x∈Ω,

y=0,x∈∂Ω.

(1)

上式中α>0是已知的量，函数φ(y)为关于y的非线性函数，φ(y)∈W(Ω)，并满足对任意的φ′(y)≥0.假设f∈L2(Ω)，yd∈L2(Ω),B是从ΩU到Ω上的一个连续线性算子.

2 变分形式和最优性条件

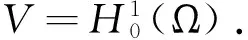
问题(1)相应的变分形式为：

(2)

a(y,v)+b(u,v)=(f,v),∀v∈V,

(3)

(y,u)∈Y×Uad.

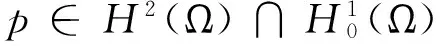
a(y,v)+b(u,v)=(f,v),∀v∈V,

(4)

a(ψ,p)=-(y-yd,ψ),∀ψ∈V,

(5)

(αu-B*p,w-u)U≥0,∀w∈Uad,

(6)

其中B*是B的伴随算子[15]，(·,·)U表示U中的内积.

3 离散格式

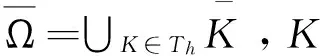
Vh=Yh={y∈L2(Ω),y|K∈P1(K),K∈Th}.

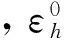
[y]=yK1|E·nK1+yK2|E·nK2，

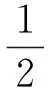
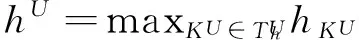
Uh= {u∈L2(Ω),u|KU∈P1(KU),

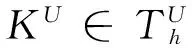
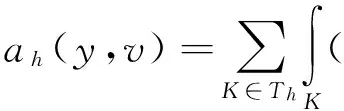
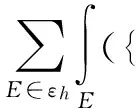
其中σ>0是内罚项.

那么，最优控制问题(4)～(6)的间断有限元逼近为：寻找三元组(yh,uh,ph)使得：

ah(yh,vh)+bh(uh,vh)=(fh,vh),

∀vh∈Vh,

(7)

a(ψh,ph)=-(yh-yd,ψh),∀ψh∈Vh,

(8)

(9)

4 数值实验

在问题(1)中取Ω=ΩU=(0,1),φ(y)=y3,B=I，其中I为恒等算子.f=(π2-1)sinπx+sin3πx，yd=(1-π4)sinπx+3sin3πx.状态变量、对偶变量和控制变量的真解为y=sinπx，u=max(p,0),p=-sinπx.

利用间断有限元方法(7)-(9)进行求解，σ=6.对非线性方程组采用牛顿迭代法求解.表1中给出了数值解的误差情况.

实验数据表明,间断有限元方法能有效求解最优控制问题(1).

表1 间断有限元方法求解的数值解误差

[1] W. Liu and N. Yan, Adaptive Finite Element Methods for Optimal Control Governed by PDEs, Beijing: Science Press, 2008.

[2] Y. Chen and Z. Lu, High Efficient and Accuracy Numerical Methods for Optimal Control Problems[J].Beijing: Science press, 2015.

[3] Y. Chen, Y. Huang, W. Liu and N. Yan, Error Estimates and Superconvergence of Mixed Finite Element Methods for Convex Optimal Control Problems[J].J. Sci. Computing, 2010,42(3):382-403.

[4] W. Zhang and H. Ma, The Chebyshev-Legendre Collocation Method for a Class of Optimal Control Problems[J]. Int. J. Comp. Math., 2008,85(2):225-240.

[5] Y. Chen and F. Huang, Galerkin Spectral Approximation of Elliptic Optimal Control Problems with H1-norm State Constraint[J]. J. Sci. Comp., 2016(67):65-83.

[6] Y. Chen, N. Yi, and W. Liu, A Legendre Galerkin Spectral Method for Optimal Control Problems Governed by Elliptic Equations[J]. SIAM J. Numer. Anal., 2008,46(5):292-315.

[7] J. Zhou, Improved Optimal Conditions and Iterative Parameters for the Optimal Control Problems with an Integral Constraint in Square[J].J.Comp.Appl.Math.,2016,307(1):367-373.

[8] C.Meyer and A. Rosch,Lestimates for Approximated Optimal Control Problems[J]. SIAM J. Control. Optim., 2005(44):1636-1649.

[9] C. Meyer and A. Rosch,Superconvergence Properties of Optimal Control Problems[J]. SIAM J. Control. Optim., 2004,43(3):970-985.

[10] P. Merino, Finite Element Error Estimates for an Optimal Control Problem Governed by the Burgers Equation[J]. Comp. Opt. Appl., 2016,63(3):793-824.

[11] B. Rivière, J. Tan and T. Thompson, Error Analysis of Primal Discontinuous Galerkin Methods for a Mixed Formulation of the Biot Equations[J]. Comp. Math. Appl., 2017,73(4):666-683.

[12] A. Ern, I. Mozolevski and L. Schuh, Discontinuous Galerkin Approximation of Two-phase Flows in Heterogeneous Porous Media with Discontinuous Capillary Pressures[J]. Comp. Meth. Appl. Mech. Eng., 2010,199(23-24):1491-1501.

[13] J. Kou and S. Sun, Analysis of a Combined Mixed Finite Element and Discontinuous Galerkin Method for Incompressible Two Phase Flow in Porous Media[J]. Math. Meth. Appl. Sci., 2014,37(7):962-982.

[14] J. Zhang, J. Zhu, R. Zhang, D. Yang and A. Loula, A Combined Discontinuous Galerkin Finite Element Method for Miscible Displacement Problem[J]. J. Comp. Appl. Math., 2017,309(1):44-55.

[15] J. Lions, Optimal Control of Systems Governed by Partial Differential Equations[M]. Berlin: Springer, 1971.

ADiscontinuousGalerkinMethodForaKindofNonlinearOptimalControlProblems

YANG Ji-ming, ZHU Xian-rui

(College of Science, Hunan Institute of Engineering, Xiangtan 411104, China)

For a kind of nonlinear optimal control problem, a discontinuous Galerkin method is investigated for discretization. The numerical experiments show that the discontinuous Galerkin approximation is effective to solve the optimal control problem under consideration.

optimal control; discontinuous Galerkin methods; nonlinear

O241.8

A

1671-119X(2017)03-0037-03

2017-04-01

湖南省教育厅科研资助项目(14A034);湖南工程学院2017年大学生研究性学习和创新性实验项目(校教字[2017]18号文69号).

杨继明(1975- )，男，博士，教授，研究方向：微分方程数值解法.