融雪型洪水量级的流域积温分布模型研究及应用
曹开军, 龙爱华, 王建虎, 刘洋,4, 蔡思宇, 李扬
(1.中国科学院 新疆生态与地理研究所,新疆 乌鲁木齐 830011; 2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038; 3.新疆师范大学 教育科学学院,新疆 乌鲁木齐 830054; 4.新疆大学 资源与环境科学学院,新疆 乌鲁木齐 830046)
融雪型洪水量级的流域积温分布模型研究及应用
曹开军1, 龙爱华2, 王建虎3, 刘洋1,4, 蔡思宇2, 李扬1
(1.中国科学院 新疆生态与地理研究所,新疆 乌鲁木齐 830011; 2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038; 3.新疆师范大学 教育科学学院,新疆 乌鲁木齐 830054; 4.新疆大学 资源与环境科学学院,新疆 乌鲁木齐 830046)
鉴于对高寒山区融雪洪水预警精度的迫切需求,利用能量守恒原理和水量平衡原理,选取经典分布式水文模型反序架构,构建了基于融雪型洪水量级下的积温阈值及流域积温分布模型。首先利用流域集总算法计算流域面的平均积温,然后基于气温直减率进行分配,最终确定积温分布,该模型在本质上属于热传导方程的逆问题。在模型驱动数据方面,采用NCAR再分析资料用于模拟输出流域的总体平均温度,同时利用高光谱遥感数据计算出流域平均雪深,结合对新疆地区天山北坡中段军塘湖流域长期的雪特性观测、SWAT及DHSVM径流模拟试验中径流和下渗的相关性试验数据,获得了诱发得到的4次融雪型洪水过程流域的积温分布特征。最后,根据气温直减率,确定军塘湖流域面上的积温分布特征。在对研究区4场融雪型洪水进行模拟验证后发现,该模型的输出结果较为精确(纳什效率系数NSE为0.815)。然而由于模型的水文过程(下渗、蒸发等)仍存在一定的不确定性因素,因而模型结果与实际观测结果依旧存在一定差异(算术平均误差为10.65%)。研究认为,该积温模型的研制对于空间气象站点缺少区的高纬度融雪型洪水多发区的预警、预报具有较大的理论价值及应用价值。
高寒山区;积温分布模型;军塘湖流域;融雪洪水预警
洪水灾害长期以来就是人类生产、生活及社会经济发展的重大威胁之一。其中,融雪型洪水灾害常发生在一些中高纬度地区及高寒山区,如我国东北、西北地区,俄罗斯、北欧、北美北部,南美西南部等国家和地区。以上区域冬季漫长且严寒,积雪丰厚,融雪期气温急剧上升将使积雪在短期内大量融化,一旦融雪水从雪盖出流将使地面积水,易形成融雪型洪灾。融雪型洪水不但直接造成社会经济损失,而且严重破坏生态环境[1]。
影响融雪洪水大小及产流过程的主要因素有:积雪的面积、深度、雪密度、吸收的热量(其中主要为太阳辐射热),雪盖的持水能力,积雪场的地形、地貌、方位,冻土深度,气候及土地覆被/利用情况等。以上因素之间亦有较复杂的交叉影响。经分析可知:在融雪期,雪盖及周围环境的能量交换将引起地面积雪层的变化。进一步分析发现:融雪型洪水量级与流域内的气温要素紧密相关[2]。若根据洪水量级确定某时段内的积温预警阈值,可提前数小时提供有效预警信息,并确定精准的融雪分布区域,以便采取必要的保护及预警措施[3]。
融雪径流模型在模拟过程中遵循能量平衡原理和水量平衡原理,按照能量传递的自然顺序来研究水文过程的演化过程或分布状态,起到了由因推果的作用,该架构设计思想属正演问题建模。例如:美国陆军工程团、美国气象局及美国国家气象服务局于1983年构建的融雪模型PRMS(Precipitation Runoff Modeling System)[4],该水文模型基于能量平衡原理,具有一定的物理机制和分布式参数。它可以将一个大流域离散为几种土地覆盖类型,每种类型的积雪融化机制具有类似特征。PRMS中的融雪算法反映了雪盖表层条件变化的速度远远大于雪盖下层条件变化的速度。PRMS还考虑了森林对积雪的冠层截留及积雪融化的影响。传统模型中的融雪计算过程主要用于评价水量平衡、洪峰流量和流域内土壤水含量等地表过程的变化。模型输入数据包含了流域下垫面的各类参数(如地貌、植被类型、土壤类型及水文特征等)及气候驱动数据[5]。近年来,国内外涌现出众多水文模型或融雪模块,如:MIKE-SHE(System Hydrological European)、SWAT(Soil and Water Assessment Tool)、DHSVM(Distributed Hydrology Soil Vegetation Model)及VIC(Variable Infiltration Capacity)等[6-11],它们大部分均基于正演问题建立计算模块。
本文尝试根据流域的融雪型洪水持续的时间尺度与洪水量级等要素,反演出流域积温阈值及其融雪空间积温分布,以最终服务于融雪型洪水预警应用。
1 模型概况
1.1 积温反演
融雪型洪水预警的核心问题是根据某时段内的融雪总量计算出雪盖表面该时段的积温值。积雪层内温度的传输过程如图1所示。

图1 积雪层温度传输过程示意图
若积雪与周围环境(主要是大气)有热交换,可用傅里叶传热方程描述:
(1)
式中:ρ为积雪密度;t为热传输的时间;CS为积雪的比热容;T为积雪层的温度梯度上某雪层温度,K;λ为积雪的热传导系数,与积雪密度ρ紧密相关;LS为积雪雪深。
积温反演是热传导方程逆问题的求解。热传导方程的逆问题求解,必须指定温度T的边界条件。若积雪在温度c时由感热阶段进入相变潜热阶段,为合理简化融雪型洪水预警阈值的计算,则取积雪雪盖表面气温为温度c时作为预警的初始时间,即:
T(z,0)=c, 0 (2) 由于积雪的潜热继续增加,进而相变成为融雪水。在某时段t内积雪融雪水量的相变潜热总和Q即为此融雪阶段的热通量,即: (3) 根据模型假设,潜热变化阶段积雪底层温度为f(t),则有: T(LS,t)=f(t),t≥0。 (4) 用偏微分方程有限差分法的Crank-Nicholson隐式差分方法数值计算方程(1),由方程(2)(3)(4)可计算出积雪层在融雪时期变化下的温度梯度T(z,t)及积雪表面的温度T(0,t)。数值模拟可利用MATLAB 2014a完成,以上过程即一维热传导方程的逆问题的求解。 1.2.1 积雪的感热阶段计算 积雪融雪期的最初阶段是感热阶段。在这一阶段,积雪吸收热量,直至积雪垂直方向上各层达到0 ℃,并且垂直层不存在温度梯度的变化。感热总量的计算式为: QS=-CSρSLS(TS-Tm)。 (5) 式中:QS为感热总量;CS为雪的比热容,本研究取值为2 009 J/(kg·K);ρS为积雪密度;TS为雪盖表层温度;Tm为融雪临界高程处的温度。由于本文的预警起始时间选取在积雪已经历了感热阶段后,故该阶段的能量变化将不考虑,也不计算。 1.2.2 洪水水量相变焓计算 融雪过程的感热阶段结束后,积雪若再持续吸收热量,将进入相变阶段。该阶段中,积雪的含水率将持续上升,当积雪中含水量超过积雪最大持水量时,将发生融雪水出流现象。 汛期时的融雪水总量,可近似认为是洪水水量与下渗量之和。因而根据水量平衡原理可计算出其相变焓(相变潜热), Qen=mSCS(Tf-Ti)。 (6) 式中:Qen为相变焓;mS为融雪水总质量;CS为雪的比热容,这里取值为33.4 kJ/(kg·K);Ti、Tf分别为融雪期初期、末期的雪盖温度。 由于积雪层不是稳定的固态层,其热传导系数随积雪层的湿度变化而变化。雪发生相变时,积雪融化成水,若超过雪层的最大持水能力,将会发生流失现象,并带走相当的热量。因而,积雪传热不同于经典的传热问题。此外,为减少模型的复杂度,定义了有效热传导系数kS。结合试验区的观测结果,将雪密度ρS和有效热传导系数kS之间的关系用拟合函数表示为: 式中kS的单位为W/(m·℃);积雪密度ρS可由架设在试验区的积雪特性仪测得。 若知道流域内的平均气温及气象站观测气温值,可确立流域内各观测位置的温度分布,以最终确定融雪强度的分布。点i处的温度Ti根据点j处的温度Tj确定, Ti=Tj+a(zi-zj)。 (7) 式中:a为气温递减率,根据经验和实地观测,流域内整体气温递减率为0.005 9 ℃/m;zi、zj分别为观测点i、j处的高程。 若气温超过0 ℃,积雪开始融化,海拔高程带上的融雪临界高程zm可通过下式计算: zm=zaws+a-1(Taws-Tm)。 (8) 式中:Taws为在海拔zaws高程处的观测气温;Tm为融雪临界高程所具有的温度。 选择地处新疆天山北坡昌吉州呼图壁县内的军塘湖流域为典型研究区,如图2所示。军塘湖河是天山西段呼图壁县境内的一条小河,发源于天山北坡特尔斯盖南缘三道马场以西的特力斯喀达坂。通过ArcGIS工具的统计分析可知,流域源头的高程约3 400 m,全流域大部分高程在1 000~1 500 m范围内,流域平均海拔高程为1 360.31 m。河网在低山带的纳札尔汇合,流经呼图壁县西部的前山丘陵后进入平原,在出山口汇入红山水库。军塘湖河从源头至红山水库河长约45.20 km,红山水库以上集水面积为833.57 km2,流域平均高程为1 503 m,东西沟两大支流汇合口以上河道纵坡降为62.5‰,汇合口以下至红山水库河道纵坡降为52.6‰,多年平均年径流量为3.89×108m3,经水库调节后,被下游灌区所引用[9]。自每年9月中旬开始,流域高山地区会出现积雪;随着气温、地温的下降,次年1月积雪深度达到最大值;2月,气温、地温开始回升,积雪开始融化;3月,积雪开始大面积融化。军塘湖河径流量年内分配不均匀,春季来水量最大。其中,初春3月为全年来水量最大月,这期间的河道来水除了由山区泉水和地下水作为基流稳定补给外,主要是由中低山带的季节性积雪融化补给,表现出天山北坡地区小型河流的重要特点,并可分为径流形成区和径流散失区,两区的分界线在河流出山口附近。选择该流域,一是因为其流域面积小且基本闭合,流域完整且特征典型,符合研究目的;二是近年来该流域融雪洪水发生较为频繁且典型。 图2 研究区位置图 采用新疆军塘湖流域的资料对积温分布模型进行测试。其中,气象数据资料依赖于军塘湖流域架设的自动气象观测站,军塘湖试验点已观测了11 a(2004—2014年)。试验区内架设的3处气象站在融雪期可进行逐小时尺度的气象观测及记录工作。观测内容包括区域的长波和短波辐射、降水、气温、风速、大气压强和空气湿度。 模型所用的温度值为整个流域内的平均气温。由于气象观测站点在山区的分布较稀疏,本研究利用美国国家大气研究中心(National Center for Atmospheric Research,NCAR)的再分析资料,结合WRF(Weather Research and Forecasting)模式填补流域内栅格尺度的平均气温的分布情况。本研究中的WRF模式参数化物理方案是基于长期的融雪期观测确定的,经验证,其模拟气温误差低于13.5%[10]。 雪覆盖下的各层土壤的温度及湿度指标利用土壤水分温度电导率测量仪EM50进行测量。每个观测点均埋设一部EM50,观测纵深分别为5、10、15、20、25、30 cm。由于冻土层的存在,同时由于积雪具有较低的热传导度,相对于净辐射、湍流交换能量等,地热对融雪过程的影响更小,甚至可忽略。然而对于长时期的地热而言,尤其是融雪末期雪层较薄时,地热对积雪的融化作用显著。 图3 观测站点位置示意图 3.1.1 积雪深度的反演 本研究中,积雪深度的测量主要依靠地面站点观测、高光谱遥感等技术完成。 利用基于BP神经网络的融雪期积雪深度反演模型,采用实测光谱数据中与雪深相关性达到显著水平的1 456~1 568 nm和1 966~1 992 nm波段的数据作为输入数据,试验发现在1 022、1 241、1 492 nm附近为积雪特征吸收谷;每个样品的积雪深度作为输出以建立回归模型。对所建BP神经网络的训练发现:当隐含层节点数为4时,确定性系数R2为0.86,均方根误差(Root Mean Square Error,RMSE)为0.67。 积雪深度的观测值与高光谱反演结果见表1。经过对比分析发现:BP神经网络模型可以显著提升高光谱数据反演积雪深度的能力。 表1 2012年3月12日11时雪深高光谱 反演结果与观测值对比 3.1.2 积雪密度的确定 本研究发现,积雪密度与积雪深度存在较高的相关性,可用幂函数表示, (9) 式中的系数a、b可结合实地测量数据采用统计回归的方法率定,见表2。 表2 系数a、b的率定结果 流域内土壤类型的分布与海拔高度存在较高的相关性,即某一类型土壤集中在某一海拔范围内。这是长期以来土壤发育过程受热蚀变和物理风化而造成的,其中,化学分解和海拔存在着密不可分的联系。因此,海拔垂直带上不同类型土壤的水力传导系数KS是在所有土壤物理参数中差异较为明显且较为重要的参数,该参数可显著影响径流下渗量。 本研究参考干旱区的自然地理状况[1]和《中国土壤数据库》,结合流域土壤取样试验,确定了所需土壤的属性参数。具体见图4、表3和表4。 图4 军塘湖流域土壤分类 土壤类型海拔高度/m栅格数分布面积百分比/%土壤类型海拔高度/m栅格数分布面积百分比/%壤质砂土2700~3441352982.46粉质壤土1170~162036550234.63砂质壤土2250~2700463625.83砂质黏壤土900~117032170532.20壤土1620~2250656486.22黏壤土/亚黏土737~90019694618.66 表4 军塘湖流域土壤类型及物理参数 注:括号内数据表示各类土壤相关物理参数的取值范围。 正演水文问题先基于某单位元尺度(如栅格尺度、水文响应单元)计算,再进行集总。而水文学逆问题的求解思路与之相反,是先进行流域集总,再基于某单位响应元尺度进行分配以最终确定分布。正演问题和反演问题均遵循热量守恒及水量平衡。逆问题求解较正演问题求解存在更大的难度,这是由于逆问题的求解往往违背了物理过程的自然顺序,从而使正问题中众多良好的性质不再满足。而这种现象在众多学科的逆问题研究中均普遍存在。因此,融雪型洪水预警模型不仅要考虑物理动力学过程,亦要结合观测经验。 选取发生在军塘湖流域内的4次融雪型洪水过程进行本研究的验证分析。其中,研究区在2011年3月26—27日和2014年3月20日发生两次较大的 融雪型洪水过程,3个观测点中仅发现观测点3的上游区域存在冻土,而此区域较小,仅占整个军塘湖流域面积的8%。本研究理想化认为流域内融雪水下渗不受冻土的影响,产流形式为蓄满产流;而发生在2012年3月12日和2013年2月27—28日的两次洪水过程,发现在观测点1的上游区域存在冻土,融雪水下渗受冻土的影响,产流形式为超渗产流。 本研究选取的4次融雪型洪水流量过程的观测时段见表5,在观测时段内的流量及拟合曲线如图5所示。 表5 融雪型洪水流量过程信息 图5 洪水流量过程拟合曲线 由图5可知,洪水量级受冻土影响显著。蓄满产流发生在土壤非冻结状态,超渗产流发生在土壤冻结状态。冻土层的存在,极大地影响了流域内融雪水的下渗过程。这主要是因为冻土中存在冰,由于冻胀作用,使土壤中水分原本所占的体积增大,则土壤中剩余孔隙度减小,融雪水可以通过这些空隙进入到土壤层的通道变小了。从图5(a)(b)(c)可以看出,洪水量级发展到10 m3/s,若流域下渗受冻土影响较小时,下渗时长约13 h,而流域下渗受冻土影响较大时,下渗时长约8 h。 融雪水的下渗是很重要的水动力过程。水从地面渗透进入土壤的过程中,受植被、土壤特性、水力传导系数、前期土壤含水量等土壤表层条件的影响。因而,下渗量具有很强的不确定性。 鉴于此,结合在研究区内利用SWAT、DHSVM模拟军塘湖流域的洪水过程[7],建立下渗量和径流量之间的相关关系,如图6所示。图中散点为SWAT或DHSVM模拟值;x为某整个洪水过程的模拟总流量;y为模拟的对应下渗总量。 图6 原始数据散点与回归直线 图6(a)蓄满产流情况:回归系数估计值的95%的置信区间为[32.471,68.457]。图6(b)超渗产流情况:回归系数估计值的95%的置信区间为[523.453,1 357.300]。 进而,根据回归方程计算出4次军塘湖流域洪水过程的累积下渗量,结果如图7所示。 图7 流域下渗量 流域总融雪水量为流域下渗量与洪水水量之和。根据流域总融雪水量,可计算出引起积雪相变潜热的总热量。计算结果如图8所示。 图8 某阶段融雪期积雪相变潜热总和 根据融雪水的相变潜热总量及流域面积,反演积雪表面的积温值。根据假设,经过感热阶段的积雪层温度为0 ℃。积雪在相变过程中底层温度保持在0 ℃,分别代入边值条件公式(2)和公式(4)后,本研究反演出洪水前后过程(0≤t≤1)流域上雪盖表面的积温值。其中,4次流量过程模型方程的输入参数及边界条件分别见表6和表7。 表6 模型方程的输入参数 表7 模型方程的边界条件 WRF模式模拟输出的雪表积温与其观测值如图9所示。 图9 洪水量级对应的气温阈值 本研究分别采用皮尔逊相关系数、算术平均误差及纳什效率系数3个特征量进行统计检验。 皮尔逊相关系数(COR): (14) 算术平均误差(RME): (15) 纳什效率系数(NSE): (16) 对于纳什效率系数(NSE),我国《水文情报预报规范》(SL 250—2000)规定:NSE≥0.90,预报精度等级为甲级;0.70≤NSE<0.90,预报精度等级为乙级;0.50≤NSE<0.70,预报精度等级为丙级;NSE<0.50,则不能满足预报要求。 3个统计检验指标的计算结果见表8。 表8 统计检验指标的计算结果 由预报积温阈值和实测积温阈值的对比结果(图9)及统计检验指标的计算结果(表9)可知,该融雪洪水阈值模式的模拟结果较好。具体表现为: 1)从模型模拟值与观测值的对比分析发现,模式预报的温度模拟值与观测值保持高度一致的变化趋势,纳什效率系数(NSE)为0.815,预报精度等级为乙级,说明在该研究区的预报效果很理想。 2)对于融雪型洪水预报中最重要的温度阈值估算问题,存在微弱低估现象,然而预报的算术平均误差(RME)为10.65%,皮尔逊相关系数(COR)为0.998 7,依然获得了较为理想的洪水预警要求。 本研究基于30 m DEM分辨率的栅格尺度,确定流域内积温的空间分布。根据关系式(7)和(8),结合海拔的气温直减率,确定零度等值线以下的区域为山体积雪的融雪分布区域,如图10所示。 图10 军塘湖流域融雪洪水的流域积温分布 出于融雪洪水预警预报的需求,结合天山北坡春季融雪洪水过程的特点,充分考虑大气水文学的耦合过程,利用一维热传导方程的反方向求解,设计并构建了融雪型洪水量级下的积温分布模型,并以新疆天山北坡的军塘湖流域进行验证。 根据设计模型的特点,一方面,采用RS、GIS及中尺度气象模式WRF等手段获得充分可靠的空间数据。主要利用DEM及NCAR/Final Analysis Data作为初始边界,利用WRF运行输出流域内的平均气温,利用GIS技术对流域数据进行空间处理及管理,最终提取水文模型所需输入的大量空间数据(土壤、积雪及流域信息等),为模型的空间数据输入提供足够的资料支持。另一方面,模型构建的水和热动力机制做到合理的简化及条件假设,使得模型贴近自然状态下的动力学过程。 本研究对2011—2014年发生在新疆天山北坡中段典型研究区(军塘湖流域)的融雪期诱发的4次融雪型洪水的积温阈值进行了模拟计算。建立了数值计算模型,通过洪水发展期的水量发展过程进行短期融雪期气温阈值估算,与实际观测进行对比分析后发现:试验结果满足融雪型洪水气温预警需求。 结合SWAT、DHSVM等模式对军塘湖流域洪水过程的多年试验,建立了下渗量和径流量之间的相关关系,进而间接估算出军塘湖流域融雪期某阶段的累积下渗量。方法略显粗糙,而进一步模型改进需要定量研究流域的气温变化下的下渗响应面积,这需要建立精度较高的积雪密度-土壤湿度数据集,需要借助微波遥感技术研究积雪层,确定积雪密度、积雪深度、积雪层含水率、积雪层雪密度分布等数据;土壤层需要在试验区增加仪器EM50,以提高测量土壤层湿度及土壤温度的空间分辨率。 本研究中的模型的相对误差为10.65%。采用本研究方法可有效地确定诱发积雪型洪水的气温积温阈值及积雪覆盖区域的融雪分布,为我国高寒山区融雪洪水预警预报提供重要参考。 [1] 陈曦.干旱区自然地理[M].北京:科学出版社,2010:226-289. [2] LEAVESLEY G H,STANNARD L G,SINGH V P.The precipitation-runoff modeling system-PRMS[J].Computer Models of Watershed Hydrology,1995,12(3):281-310. [3] GEORGAKAKOS K P,BRAS R L.A hydrologically useful station precipitation model[J].Water Resources Research,1984,20(11):1585-1610. [4] MARKSTROM S L,NISWONGER R G,REGAN R S.GSFLOW-Coupled Ground-water and Surface-water FLOW model based on the integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005):US[J].Geological Survey Techniques and Methods,2008,6(D1):240-252. [5] 孟现勇,师春香,刘时银,等.CMADS(V1.0)数据集及其在流域水文模拟中的应用:以黑河流域为例[J].人民珠江,2016,37(7):1-19. [6] MENG X Y,YU D L,LIU Z H.The comparison of the mountain snowmelt runoff simulation by using SWAT and energy balance-based model[J].Journal of Mountain Sciences,2015,12(2):368-381. [7] CHEN C X,TANG Z H.Numerical Methods of Groundwater Flow Problem[M].Wuhan:China University of Geosciences Publishing House,1994. [8] FREEZE R A,HARLAN R L.Blueprint for a physically-based digitally-simulated hydrological response model[J].Journal of Hydrology,1969,9(3):237-258. [9] 孟现勇,吉晓楠,刘志辉,等.SWAT模型融雪模块的改进与应用研究[J].自然资源学报,2014,29(3):528-539. [10] 孟现勇,刘志辉,乔鹏,等.基于栅格尺度的双层融雪径流模型研究及应用[J].水文,2013,33(4):10-15,31. [11] ABBOTT M B,BATHURST J C,CUNGE J A,et al.An introduction to the European Hydrological System—Système Hydrologique Européen,“SHE”,2:structure of a physically-based distributed modeling system[J].Journal of Hydrology,1986,87(2):61-77. ResearchandApplicationonBasinAccumulatedTemperatureDistribution(ATD)ModelattheSnowmeltFloodMagnitude CAO Kaijun1, LONG Aihua2, WANG Jianhu3, LIU Yang1,4, CAI Siyu2, LI Yang1 (1.Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China;2.State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China;3.College of Educational Science, Xinjiang Normal University, Urumqi 830017, China;4.School of Resources and Environment Science,Xinjiang University, Urumqi 830046, China) Based on the urgent demand of warning accuracy of snowmelt flood in cold highland areas, this study used the principles of conservation of energy and water balance, chose antitone structure of classic distributed hydrological model, and built accumulated temperature threshold and basin accumulated temperature distribution model at the snowmelt flood magnitude. The research firstly calculated average accumulated temperature in the basin according to basin lumped algorithm, then did allocation based on the temperature lapse rate, and finally identified accumulated temperature distribution. The model explains the inverse problem of heat conduction equation. In the aspect of model-driven data, the study adopted reanalysis data of National Center for Atmospheric Research (NCAR) to simulate the ensemble average temperature of output basin. Meanwhile, we used hyperspectral remote sensing data to compute basin average snow depth. Combined with long-term snow characteristics observation of Juntang Lake basin which located in the middle section of the north slope of Tianshan Mountain in Xinjiang area, Soil and Water Assessment Tool (SWAT) and the relative data of runoff and infiltration in runoff simulation experiments based on Distributed Hydrology Soil Vegetation Model (DHSVM), the characteristics of basin accumulated temperature distribution in the process of four induced snowmelt floods was obtained. Finally, according to temperature lapse rate, the characteristics of accumulated temperature distribution in Juntang Lake basin were identified. Overall, after simulation verification of the four snowmelt floods in the study area, the model output is found to be relatively accurate (the Nash-Sutcliffe efficiency coefficient is 0.815). However, due to the uncertainty factors of the model′s hydrological processes (such as infiltration, evaporation and so on), there are some differences between outputs and observation results (average relative error is 10.65%). The research deems that the accumulated temperature model will play an important role in the warning and forecasting of snowmelt flood in high latitude areas which lack spatial meteorological stations. cold highland area; accumulated temperature distribution model; Juntang Lake basin; snowmelt flood warning 2016-12-03 “十三五”国家重点研发计划课题(2016YFC0402208,2016YFC0401903,2016YFC0400903,2016YFC0402204,2016YFC 0402201);“十二五”国家科技支撑计划(2015BAB07B03);2016年度流域水循环模拟与调控国家重点实验室培育课题代表性成果(2016CG05)。 曹开军(1987—),男,新疆伊犁人,博士研究生,从事水资源管理方面的研究。E-mail:ckjun200@qq.com。 龙爱华(1976—),男,湖南郴州人,教授级高级工程师,博士,从事社会水循环、生态经济学、跨界河流影响等方面的研究。E-mail:ahlong@iwhr.com。 10.3969/j.issn.1002-5634.2017.05.002 TV122;P333.9 A 1002-5634(2017)05-0010-09 (责任编辑陈海涛)
1.2 融雪过程各阶段的热量计算
1.3 积雪热学属性的确定
1.4 试验区气温的空间差异性描述
2 研究区概况及数据准备
2.1 研究区概况
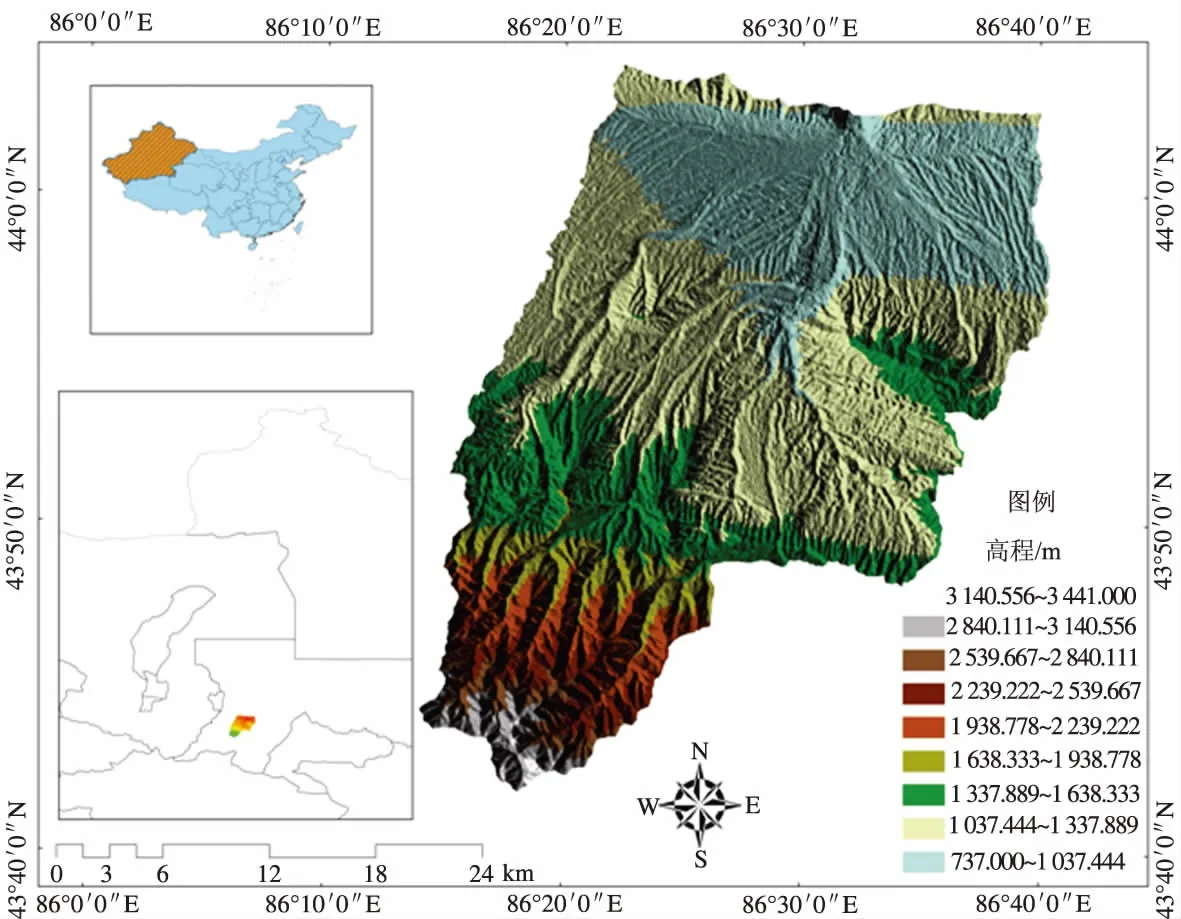
2.2 数据获取及模型参数
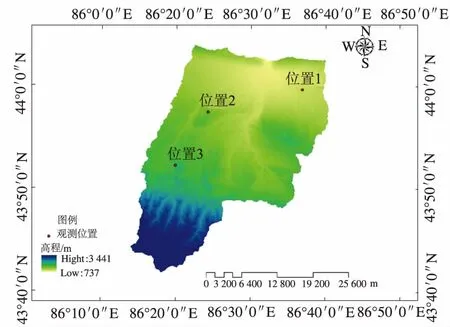
3 模型输入数据
3.1 积雪属性的确定

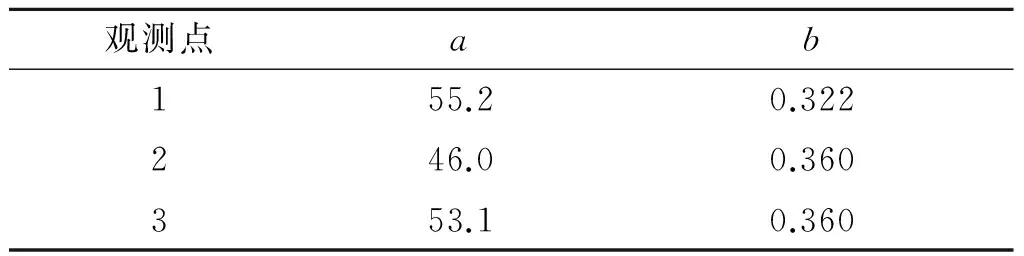
3.2 流域垂直带土壤分布及土壤属性的确定



4 模型模拟与验证结果
4.1 洪水过程


4.2 洪水期下渗过程
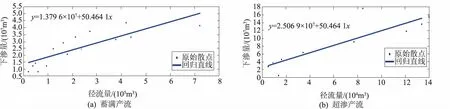

4.3 洪水期流域积雪的相变潜热

4.4 洪水期积雪表面的积温值反演
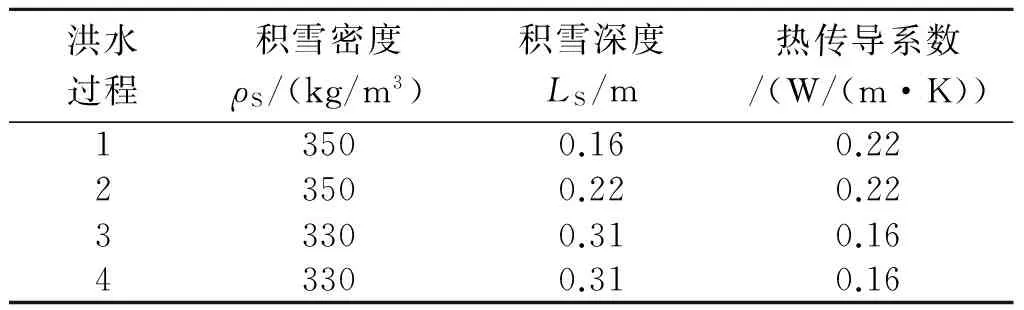


5 统计检验


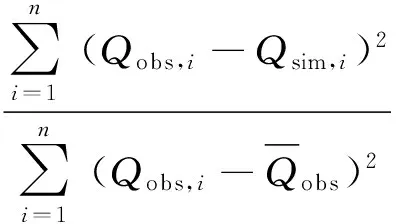


6 融雪洪水的流域积温分布


7 结语

