基于拓扑连接紧密度的相似性链路预测算法
丁大钊,陈云杰,靳彦青,刘树新
(国家数字交换系统工程技术研究中心,郑州 450002)
(*通信作者电子邮箱18603860002@126.com)
基于拓扑连接紧密度的相似性链路预测算法
丁大钊*,陈云杰,靳彦青,刘树新
(国家数字交换系统工程技术研究中心,郑州 450002)
(*通信作者电子邮箱18603860002@126.com)
许多链路预测方法仅仅关注预测的准确度衡量指标,忽略了精确度衡量标准在实际应用中的重要作用,且没有考虑共同邻居与预测节点间紧密度对相似性刻画的影响。针对上述问题,提出了一种基于拓扑连接紧密度的相似性链路预测算法。该方法通过局部拓扑结构定义共同邻居紧密度,并引入参数调节不同网络中紧密程度,最终刻画网络节点间的相似度。6个实际网络测试表明,相比共同邻居(CN)、资源分配(RA)、Adamic-Adar(AA)、局部路径(LP)、Katz等相似性指标,该算法提升了链路预测的预测精度。
复杂网络; 链路预测;紧密度;相似性;拓扑结构
0 引言
随着复杂网络研究的不断深入,越来越多的复杂系统都成为了复杂网络的研究对象[1-5]。链路预测作为网络科学领域的研究热点,主要用于预测网络中任意两个节点间连接的可能性[6]。链路预测方法在实际应用中受到广泛关注,其可以预测发现生物蛋白质网络中未知的连接[7]、预测人际关系网络中将来可能发生的连接[8]以及纠正航空运输网络中错误的统计连接[9]等。
当前,基于复杂网络拓扑演化机制,已经提出许多相关的链路预测方法。其中,基于拓扑结构的相似性方法具有简单、高效、低复杂度的特点,受到普遍关注[10]。根据算法的复杂度和涉及网络结构的范围,相似性链路预测方法可以分为局部相似性指标和全局相似性指标[11]。局部相似性链路预测方法包括直接计算共同邻居数目的共同邻居(Common Neighbor, CN)指标[12]、对共同邻居进行加权的资源分配(Resource Allocation, RA)指标[13]和Adamic-Adar (AA)[14]指标以及考虑了三阶路径的局部路径(Local Path, LP)指标[15],当然也有对RA指标的拓展(Extend Resource Allocation, ERA)[16]以及基于随机游走的链路预测方法[17],均取得了较好的效果。虽然局部相似性指标在较低的时间复杂度上取得了较好的效果,但为了进一步提高预测精度,又提出了许多全局相似性指标,如:Katz指标、LHN-II[18]指标、平均通勤时间(Average Commute Time, ACT)和余弦相似性指标[19]。虽然多数全局相似性指标能够取得较好的预测效果,但具有较高的时间复杂度,难以应用到大型实际网络中。许多相似性方法忽略了节点和共同邻居节点之间紧密性的影响,且仅仅关注准确性评价指标,缺少对精确度指标的关注。而实际网络应用如蛋白质网络的链路预测中,会更多地关注排名靠前的连接的预测精度。因此,提高链路预测方法的精确度同样具有重要的实际意义。
在人际交互网络中,如果两个陌生人和共同好友的联系紧密,其更有可能成为朋友,且联系越紧密,其成为朋友的可能性越大。图1所示两对不同的节点均包含一个共同邻居节点。根据CN、RA、AA和LP等局部相似性指标,两对节点之间存在连接的可能性是相同的。但实际情况中,由于节点与其共同邻居之间的紧密性更高(存在多个可能的连接),所以相比而言它们更有可能建立连接。因此节点间的紧密性对于链路预测的精确性起着较大的作用。

图1 不同的共同邻居拓扑结构举例Fig. 1 Example of topological structures for different common neighbors
基于上述分析,本文基于节点和共同邻居之间连接的紧密性,提出了一种基于拓扑连接紧密度的相似性链路预测算法,进而提高复杂网络中链路预测的精确度指标。在6个实际网络数据上的实验结果表明,相比CN、RA、AA、LP和Katz,该方法具有较高的预测精度。
1 相关相似性指标
相似性链路预测指标主要根据网络结构特点计算网络中两个未连接节点之间的相似程度。对于一对网络节点来说,算法标定得分值越高,其相似性越高,即存在连接的可能性越大。基于相似性的链路预测方法较多,以下将主要介绍CN、RA、AA和LP四个局部相似性指标以及Katz全局相似性链路预测方法。
1)CN[12]。通过共同邻居的数目衡量任意未连接的两个节点vx和vy的相似度,以Γ(x)表示节点vx的邻居集合,则共同邻居指标表示为:
(1)
2)AA[14]。在CN的基础上根据共同邻居节点的度为每个节点赋予一个权重,而权重为该节点度的对数分之一,定义为:
(2)
3)RA[13]。对于未连接的两个节点vx和vy,从vx经过共同邻居传递部分资源到vy,共同邻居传递资源的多少和其节点度成反比,则相似度描述为:
(3)
4)LP[15]。在二阶路径(共同邻居)上,考虑了三阶路径对相似性的贡献:
s=A2+αA3
(4)
其中:A为网络的邻接矩阵,α则为调节参数。
5)Katz。考虑了未连边节点之间的所有路径,表示为:
(5)

上述指标中,CN、RA、AA和LP为局部相似性指标,而Katz则为全局相似性指标,复杂度较高。
2 基于节点间紧密性的相似性链路预测指标
对于一个无权无向网络G(V,E),V和E分别为网络中点和边的集合。每一个链路预测算法给任意一对网络节点x和y分配一个分数值sxy用于衡量节点x和y之间的相似性,即存在连接的可能性。在实际网络预测中,通过分数值的高低便可确定连边可能的大小。
网络节点之间的紧密性往往与节点之间存在间接联系的数目有关,共同邻居节点作为大多数相似性指标最为关注的对象,其和两个端点之间的拓扑结构是影响相似性的主要根源。图2所示,z1和z2分别为节点x和y的共同邻居节点。对于共同邻居和节点x之间的紧密性来说,虽然两个共同邻居节点具有相同的节点度(连边数目),但由于z1与x之间存在更多的相关边,因此紧密性R(z1,x)>R(z2,x)。同理,对于z1与x、y之间的紧密性来说,R(z1,x)>R(z1,y)。基于上述定性讨论,本文将从共同邻居角度分析、定义其周围拓扑结构对于端点之间的紧密性。

图2 共同邻居节点紧密性示意图Fig. 2 Schematic diagram of closeness of common neighbors
定义1 共同邻居紧密度。对于网络中的任意两个节点x和y,其共同邻居节点为z。共同邻居z和节点x的紧密度为在共同邻居z的所有邻居节点中和节点x存在直接联系的比例,具体表示为:
R(z,x)=((|Γ(x)∩Γ(z)|+1)/kz)δ
(6)
其中δ为调节参数,用于刻画不同具体网络中紧密度的强度。同理,共同邻居z和节点y的紧密度表示为:
R(z,y)=((|Γ(y)∩Γ(z)|+1)/kz)δ
(7)
紧密度R在一定程度上反映了共同邻居节点和其他节点交互的可能性,且通过一个调节强度的参数来刻画不同实际网络中共同邻居周围结构对于紧密程度的影响。在共同邻居紧密度的基础上,本文进一步提出基于节点间紧密性的相似性链路预测指标,具体定义如下:
定义2 基于节点间紧密性的相似性指标(RC)。对于一个无权无向网络G(V,E),网络中的任意两个节点x和y,z为共同邻居节点。节点x和y之间的相似性为所有共同邻居节点与其之间紧密度的求和,具体为:
(8)

具体算法步骤如下:
步骤1 输入训练集网络矩阵;
步骤2 选取一对节点i和j,其中i≠j;
步骤3 寻找节点i和j的共同邻居{z1,z2,…};
步骤4 根据式(8)计算节点间的相似度,并记录到相似矩阵的i行j列中;
步骤5 返回步骤2,直到所有网络节点对间相似度计算完毕。
算法与CN、RA的复杂度相同,均为O(n2)。相比全局性预测方法,其时间复杂度较低,可以应用于大型复杂网络中。
3 衡量指标与网络数据
本文所关注的链路预测算法衡量标准为精确度指标Precision[20]。Precision具体为前L个预测边中预测准确的比例,可以表示为:
Precision=m/L
(9)
其中:m为预测准确的个数,文中设置L=100[21]。显然,算法的Precision值越大,其预测的精度则越高。许多实际复杂网络如蛋白质网络更多地关注预测结果中排名靠前边的准确性,故越来越多的文章使用Precision作为衡量指标。
为了测试本文方法的有效性,选择了6个常用的复杂网络数据:1)Jazz[22],即爵士音乐家合作网络,网络中的节点代表音乐家,而连边则表示音乐家之间存在合作关系;2)Kohonen[23],是有关自组织映射主题或T. Kohonen的论文引用网络; 3)Hamster[24],是在hamsterster.com网页上的用户朋友关系网络,其中点表示网页用户,连边表示他们之间存在朋友关系;4)Metabolic[25],即线虫的新陈代谢网络;5)Email[26],是一个中型企业的邮件通信网络,节点为员工,连边则表示他们之间的邮件往来; 6)Yeast[27],是蛋白质相互作用网络,网络节点表示蛋白质,而边则为它们之间的相互作用关系。
上述6个网络具体的特征参数如表1所示,包含节点数目|V|、边的数目|E|、平均度〈k〉、集聚系数C和匹配系数r。在实验测试中,每个网络数据分为训练集合ET边数占比为0.9,测试集合EP则为0.1,每个测试结果均为20次结果的均值。
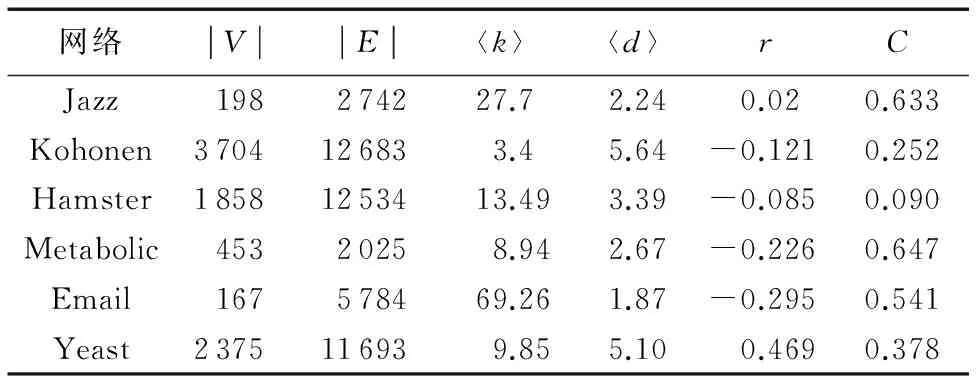
表1 实际网络的基本特征参数Tab. 1 Basic topological features of real networks
4 结果及分析
以精确度指标Precision为衡量标准,在6个实际网络中测试基于节点间紧密性的相似性指标的预测效果,具体结果分为两部分:一是不同网络中共同邻居节点集聚性对Precision结果的影响;二是与其他相似性指标的对比结果分析。
4.1 不同网络中精确度结果分析
针对6个实际网络数据,首先了分析不同网络中紧密度参数δ对RC预测结果的影响。图3中显示了δ>0时所有网络的Precision曲线。相比δ=0(此时RC即CN指标),指标均不同程度地提高了其预测精度,且在合适的参数下均可以取得最大预测精度。一般情形下,在取得最大精度值后Precision曲线都会呈现不同程度的下降。但在某些网络如Email、Yeast、Metbolic等网络中,Precision曲线会保持在一定数值之上,这一定程度上说明了在这些网络中紧密度参数在达到一定数值后对相似性的影响就相对稳定。

图3 不同网络中Precision结果Fig. 3 Results of Precision in different networks
RC指标的Precision最大精度均高于δ=0时的预测值,这说明了共同邻居的紧密度确实能够提升链路预测中的精确度Precision。同样,相比δ=1时,即共同邻居紧密度没有强度时,最大Precision精度也明显更高,这从另一个侧面表达了紧密度的强度对于Precision的提高具有重要作用。总体来说,在不同的网络数据中,RC均能够在δ>0时迅速提高预测的Precision值,且一般情形下在δ>3时取最高点,在实际应用中可在一定范围内调节,可较大程度上提高预测精度。
4.2 与其他相似性指标对比
为了进一步说明RC指标的有效性,以下将与现有的相似性指标进行对比性分析。
表2显示了各个相似性指标的Precision结果对比,其中每个结果均是20次预测的均值,每次均是独立随机产生训练集和测试集。可以看出,6个实际网络中,相比CN、RA、AA、LP等局部相似性指标和Katz全局相似性指标,RC指标具有较高的预测精度。在局部相似性指标中,CN仅仅利用了共同邻居数量这一信息,表现相对一般;RA和AA利用共同邻居的节点度进行加权,在复杂度较低的情形下,大多数网络中Precision结果明显好于CN;在考虑了三阶路径后,LP指标在多数网络中如Kohonen、Hamster等网络中均表现较好。Katz虽然考虑了网络中所有可能的路径,但其在Precision标准下与LP指标非常接近,且Katz指标的时间复杂度较高。RC指标在考虑了共同邻居与预测节点间紧密度的情况下,取得了较高的预测精度。很明显,在许多集聚系数较低的网络中,多数相似性指标预测精度较低,而RC指标可以极大限度地提高其预测精度,如在Hamster网络中CN的预测精度为0.015,而RC的预测精度为0.186,提高比率为12.4倍。此外,RC的时间复杂度较低,非常适合于大型实际网络中的链路预测。

表2 不同指标下Precision值对比Tab. 2 Comparison of Precision for different indices
5 结语
近年来,提出了大量的相似性链路预测方法,许多方法都取得了较好的预测效果。针对现有的方法在精确度衡量标准Precision上效果较差的问题,提出了一种基于拓扑连接紧密度的相似性链路预测算法。6个实际网络数据测试表明,当前方法具有较高的精确度,而且该方法的时间复杂度较低,完全可以用于大型复杂网络的链路预测。本文算法完全基于网络结构进行链路预测,下一步可以结合网络节点属性、行为等多维度信息研究大数据挖掘下的链路预测方法。
References)
[1] GAO Z-K, SMALL M, KURTHS J. Complex network analysis of time series [J]. Europhysics Letters, 2017, 116(5): 50001-50005.
[2] LIU S, JI X, LIU C, et al. Similarity indices based on link weight assignment for link prediction of unweighted complex networks [J]. International Journal of Modern Physics B, 2016, 31(2): 1650254.
[3] ZHANG Y, BAO Z, CAO Y, et al. Long-term effect of different topology evolutions on blackouts in power grid [J]. International Journal of Electrical Power & Energy Systems, 2014, 62(2014): 718-726.
[4] 刘树新,季新生,刘彩霞,等.一种信息传播促进网络增长的网络演化模型[J].物理学报,2014,63(15):158902. (LIU S X, JI X S, LIU C X, et al. A complex network evolution model for network growth promoted by information transmission [J]. Acta Physica Sinica, 2014, 63(15): 158902.
[5] PECH R, HAO D, PAN L, et al. Link prediction via matrix completion [J]. Europhysics Letters, 2017, 117(3): 38002.
[6] WANG P, XU B W, WU Y R, et al. Link prediction in social networks: the state-of-the-art [J]. Science China Information Sciences, 2015, 58(1): 1-38.
[7] VON MERING C, JENSEN L J, SNEL B, et al. STRING: known and predicted protein-protein associations, integrated and transferred across organisms [J]. Nucleic Acids Research, 2005(33): D433-D437.
[8] SCELLATO S, NOULAS A, MASCOLO C. Exploiting place features in link prediction on location-based social networks [C]// KDD ’11: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2011: 1046-1054.
[9] HOLLAND P W, LASKEY K B, LEINHARDT S. Stochastic blockmodels: first steps [J]. Social Networks, 1983, 5(2): 109-137.
[10] FENG X, ZHAO J C, XU K. Link prediction in complex networks: a clustering perspective [J]. The European Physical Journal B, 2012, 85: 3.
[11] LÜ L, ZHOU T. Link prediction in complex networks: a survey [J]. Physica A: Statistical Mechanics and its Applications, 2011, 390(6): 1150-1170.
[12] LORRAIN F, WHITE H C. Structural equivalence of individuals in social networks [J]. The Journal of Mathematical Sociology, 1971, 1(1): 49-80.
[13] ZHOU T, LÜ L, ZHANG Y-C. Predicting missing links via local information [J]. The European Physical Journal B, 2009, 71(4): 623-630.
[14] ADAMIC L A, ADAR E. Friends and neighbors on the Web [J]. Social Networks, 2003, 25(3): 211-230.
[15] LÜ L, JIN C-H, ZHOU T. Similarity index based on local paths for link prediction of complex networks [J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2009, 80(4): 046122.
[16] LIU S, JI X, LIU C, et al. Extended resource allocation index for link prediction of complex network [J]. Physica A: Statistical Mechanics and its Applications, 2017, 479: 174-183.
[17] 刘思,刘海,陈启买,等.基于网络表示学习与随机游走的链路预测算法[J/OL].计算机应用,2017 [2017- 04- 01]. http://www.joca.cn/CN/abstract/abstract20373.shtml. (LIU S, LIU H, CHEN Q M, et al. Link prediction algorithm based on network representation learning and random walk [J/OL]. Journal of Computer Applications, 2017 [2017- 04- 01]. http://www.joca.cn/CN/abstract/abstract20373.shtml.)
[18] LEICHT E A, HOLME P, NEWMAN M E J. Vertex similarity in networks [J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2006, 73(2): 026120.
[19] FOUSS F, PIROTTE A, RENDERS J-M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation [J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(3): 355-369.
[20] HERLOCKER J L, KONSTAN J A, TERVEEN L G, et al. Evaluating collaborative filtering recommender systems [J]. ACM Transactions on Information Systems, 2004, 22(1): 5-53.
[21] LÜ L, ZHOU T. Link prediction in weighted networks: the role of weak ties [J]. Europhysics Letters, 2010, 89(1): 18001.
[22] GLEISER P M, DANON L. Community structure in Jazz [J]. Advances in Complex Systems, 2003, 6(4): 565-573.
[23] ZHANG Q, LÜ L, WANG W, et al. Potential theory for directed networks [J]. PLoS ONE, 2013, 8(2): e55437.
[24] LÜ L, PAN L, ZHOU T, et al. Toward link predictability of complex networks [J]. Proceedings of the National Academy of Sciences, 2015, 112(8): 2325-2330.
[25] DUCH J, ARENAS A. Community detection in complex networks using extremal optimization [J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2005, 72(2): 027104.
[26] MICHALSKI R, PALUS S, KAZIENKO P. Matching organizational structure and social network extracted from email communication [C]// BIS 2011: Proceedings of the International Conference on Business Information Systems. Berlin: Springer-Verlag, 2011: 197-206.
[27] BU D, ZHAO Y, CAI L, et al. Topological structure analysis of the protein-protein interaction network in budding yeast [J]. Nucleic Acids Research, 2003, 31(9): 2443-2450.
This work is partially supported by the National High Technology Research and Development Program (863 Program) of China (2015AA01A708, 2016YFB080160).
DINGDazhao, born in 1979, M. S., engineer. His research interests include communication and information system.
CHENYunjie, born in 1981, M. S., engineer. His research interests include wireless communication security.
JINYanqing, born in 1983, engineer. Her research interests include wireless communication.
LIUShuxin, born in 1987, Ph. D. His research interests include complex network.
Linkpredictionmethodforcomplexnetworkbasedonclosenessbetweennodes
DING Dazhao*, CHEN Yunjie, JIN Yanqing, LIU Shuxin
(NationalDigitalSwitchingSystemEngineeringandTechnologicalR&DCenter,ZhengzhouHenan450002,China)
Many link prediction methods only focus on the standard metric AUC (Area Under receiver operating characteristic Curve), ignoring the metric precision and closeness of common neighbors and endpoints under different topological structures. To solve these problems, a link prediction method based on closeness between nodes was proposed. In order to describe the similarity between endpoints more accurately, the closeness of common neighbors was designed by considering the local topological information around common neighbors, which was adjusted for different networks through a parameter. Empirical study on six real networks show that compared with the similarity indicators such as Common Neighbor (CN), Resource Allocation (RA), Adamic-Adar (AA), Local Path (LP) and Katz, the proposed index can improve the prediction accuracy.
complex network; link prediction; closeness; similarity; topological structure
TP393.02
A
2017- 02- 24;
2017- 05- 06。
国家863计划项目(2015AA01A708, 2016YFB0801605)。
丁大钊(1979—),男,河南许昌人,工程师,硕士,主要研究方向:通信与信息系统; 陈云杰(1981—),男,河南新乡人,工程师,硕士,主要研究方向:无线通信网络安全; 靳彦青(1983—),女,河南南召人,工程师,主要研究方向:无线通信; 刘树新(1987—),男,山东潍坊人,博士,主要研究方向:复杂网络。
1001- 9081(2017)08- 2129- 04
10.11772/j.issn.1001- 9081.2017.08.2129

