基于ANSYS对FRP加固梁的非线性分析

程光福，杨永山

（山东科技大学土木工程与建筑学院，山东 青岛，266590）

基于ANSYS对FRP加固梁的非线性分析

程光福，杨永山

（山东科技大学土木工程与建筑学院，山东 青岛，266590）

基于有限元软件ANSYS，以3根玄武岩纤维布（BFRP）加固梁的试验为依据，通过选取合适的单元类型及收敛准则对纤维复合材料(FRP)加固梁的抗弯性能进行了非线性分析。分析结果表明，通过有限元软件模拟加固梁的破坏性形式与实际试验结果相一致；利用ANSYS可以很好地模拟纤维复合材料加固梁在承载过程中的荷载效应（跨中承载力-挠度曲线、开裂荷载及极限荷载等），计算与试验结果误差在10%以内，为实际工程提供了参考。

有限元；玄武岩纤增强材料（BFRP）；非线性；加固

研究背景及现状

纤维增强复合材料（FRP）是由基体和增强纤维两部分组成，其抗拉强度较高，但是塑性变形较小，易发生脆断。主要分为碳纤维复合增强材料（CFRP）、玄武岩纤维复合增强材料（BFRP）以及玻璃纤维复合增强材料（GFRP）。随着技术的进步，已经不断应用于建筑领域。

和碳纤维对比，玄武岩纤维材料耐高温、抗腐蚀性能好、延性高且价格低廉（仅为碳纤维成本的1/6），具有更加广阔的发展与应用空间[1]，并且被列为我国中长期要重点发展的四大高新纤维技术之一[2]。

利用有限元软件对碳纤维布加固RC梁性能的模拟与分析，很多学者已经做出了卓有成效的成果[3-5]，但关于对玄武岩纤维布对加固梁性能的分析则较少。BFRP的抗拉强度虽略低于CFRP，但是其弹性模量要高于CFRP。通过在梁底部或侧面粘贴BFRP对梁进行加固时，混凝土的弹性模量（约2×104MPa）与BFRP的弹性模量（约91GPa）有较大差异，导致两者形成的刚度矩阵差异较大，这增加了利用有限元软件求解收敛的困难性。

1 试验简介

1.1 试验设计[6]

选取文献[6]中的三根试验梁作为依据，构件的尺寸及配筋如图1所示。梁的截面尺寸，跨度3000mm，净跨 2700mm。试验中钢筋均选用HRB335级钢筋，配筋率为1.34%。其中，受拉钢筋、架立筋与箍筋的直径分别为16mm、10mm、6.5mm。试验加载方式为三分点对称加载，由分配梁传递荷载至加载点。梁仅在剪弯段配置箍筋，箍筋间距为100mm。梁的编号及加固方式，见表1。

图1 构件尺寸及配筋图

表1 梁的编号及加固方式

1.2 材料的力学性能

混凝土的设计强度为C30，混凝土立方体试块实测强度平均值为34.19N/mm2。混凝土的轴心抗拉强度取我国规范[7]中采用的计算式：

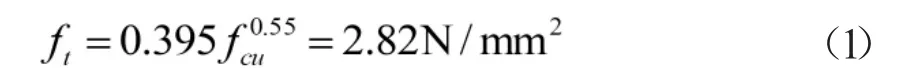
钢筋的实测平均强度为390N/mm2。玄武岩纤维技术指标，见表2。

表2 BFRP技术指标

2 有限元分析

2.1 单元类型的选择

模拟混凝土的单元选取为8个节点定义的空间实体单元SOLID65，可模拟无筋或加筋的实体结构，具有受拉开裂（拉裂）和受压破碎（压碎）的性能。采用由2个节点定义的三维杆单元LINK180来模拟钢筋，该单元能够轴向拉压但不能承受弯矩。为了避免加载点以及支座处出现应力集中现象而导致混凝土过早开裂，分别在加载点处和支座处增加了刚性垫块，选用SOLID185单元进行模拟。其尺寸分别为200mm×150mm×40mm与100mm×150mm×40mm。BFRP选用无平面外弯曲刚度的SHELL41单元进行模拟。

2.2 本构关系的选取

1）混凝土的单轴受压应力应变关系为美国Hognestad[8]建议的模型，见图2。曲线方程为

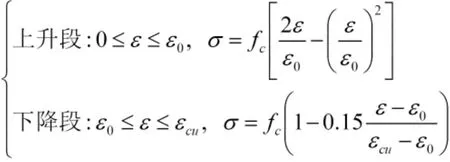
式中：fc为混凝土棱柱体抗压强度；ε0为峰值应变，取ε0=0.002；εcu——极限应变，取ε0=0.0038。

2）混凝土的破坏准则为修正的Willam-Warnke五参数准则。

3）钢筋的应力应变关系为理想弹塑性。

4）玄武岩纤维布的应力应变关系为理想线弹性，即

图2 混凝土应力应变曲线

2.3 网格划分及收敛准则

1）由于试件尺寸及加载方式的对称性，故选取1/2模型建模。假设梁符合平截面假定且钢筋与混凝土之间粘结性能良好，忽略钢筋与混凝土之间的相对滑移。由于ACFB-1与ACFB-2的破坏方式均为纤维布被拉断，混凝土与纤维布之间未发生剥离破坏，因此建模时通过耦合节点的方式使玄武岩纤维布与混凝土共同工作。混凝土的尺寸划分为50mm×25mm×25mm的正六面体（在支座处网格划分加密）。为了激活大变形选项，将梁底部的BFRP划分为三角形单元。网格划分后形成的有限元模型，见图3。

图3 钢筋应力应变曲线

2）求解过程中，共分为200个荷载子步进行加载。打开大变形选项，采用残余力的2-范数（使所有自由度的不平衡力、力矩的平方和的平方根检查收敛）收敛准则，收敛容差为0.05，迭代次数为40次。

图4 有限元模型

3 结果对比与分析

3.1 梁的承载力对比

梁承载力的试验值与有限元模拟值对比，见表3。跨中荷载-挠度曲线对比，见图4。

表3 试验值与有限元模拟值对比

图5 跨中荷载-挠度曲线

对于梁ACB-1，由图4-(a)可以看出，跨中荷载在达到24kN时荷载-挠度曲线出现了第一个转折点，此时梁跨中出现了第一条竖向裂缝导致粱自身刚度下降，跨中挠度有所增加。随后，在跨中荷载达到130kN时曲线出现了第二个明显的转折点。这是因为此时受拉钢筋已经屈服，裂缝急剧开展，跨中挠度迅速增大，此时达到了极限荷载。混凝土开裂前，有限元模拟数据与试验数据曲线基本保持一致；随着钢筋应力的不断增加，二者曲线呈现出微小偏差。对比二者曲线可以发现，数值模拟的梁的刚度要大于实际试验结果。这是因为在实际试验过程中二者会随着加载过程产生相对滑移，但是在有限元模拟假定了钢筋与混凝土连接良好，因此模拟的跨中挠度值小于试验数值。

对于梁 ACFB-1，由图 4-（b）可以看出,在荷载达到26kN时，曲线出现第一个拐点，此时受拉区混凝土开裂。当加载达到126kN时，受拉钢筋应力已经达到390MPa（见图5），此时受拉钢筋已经屈服。当加载到144kN时，通过读取最后一个荷载子步的结果，并绘制梁底BFRP的等效Mises应力云图（见图6）可以观察到：BFRP最右端（即跨中）的应力达到2179MPa，超过了其拉伸强度（2100MPa）。故认为此时BFRP被拉断，梁发生破坏，这与试验结果相符。梁开裂荷载的数值模拟结果与实际试验结果相差较大，为13.3%；极限荷载则较为吻合，两者约相差5.1%。

对于梁ACFB-2（分析同ACFB-1），梁开裂荷载的模拟结果和试验结果与ACFB-1相同，均未发生变化；而其极限荷载模拟则更为接近，两者误差为2.1%。由此可见，忽略纤维布与混凝土之间的滑移会导致小程度上高估梁的承载力，但是其在可接受的范围之内。对于这种破坏模式，由于受拉钢筋达到了屈服强度，BFRP被拉断，随后受压区混凝土的压应变达到极限压应变，充分利用了混凝土的抗压强度，因此是一种较为理想的破坏形式。

图6 屈服荷载时钢筋应力分布

图7 极限荷载时纤维布应力分布

基于上述分析可见对于梁的极限承载力而言，有限元数值分析结果与试验结果较为吻合。但对加固梁的开裂荷载而言，数值模拟与试验结果相差则略大，约13.3%。这是因为（1）纤维布的弹性模量比较高，并且在梁发生开裂前（见图7）应力较低，因此其拉伸应变较小，从而导致BFRP发挥作用有限，因此对梁的开裂荷载的提高较小。在实际试验过程中，由于在梁底粘贴BFRP，这增加了梁的抗弯刚度，进而延缓了截面中和轴的上升，因此一定程度上延缓了梁的开裂。（2）第一条裂缝可能出现在梁内部，而试验过程中是以观察到梁表面出现第一条裂缝时所对应的荷载为开裂荷载，这也导致了二者之间的差异。

3.2 纤维布应力对比

梁ACFB-2开裂前与开裂后梁底BFRP的应力，分别见图7与图8。从图8中可以看出：梁在开裂之前纤维布应力水平较低，最大应力位于跨中，约80.66MPa；沿梁长方向，BFRP应力从跨中至支座处逐渐递减至4.8MPa，且沿梁宽度方向应力分布均匀。观察开裂后梁底BFRP应力云图可以发现，梁在开裂以后，BFRP的应力迅速增长；跨中BFRP的应力达245.82MPa，相比开裂前提高了约170%。端部BFRP应力较小，这时梁底部BFRP的应力不再沿梁长度均匀变化，在跨中与加载点处应力较大。这说明混凝土在开裂之前，BFRP几乎不承担力的作用。随着裂缝增长，受拉区混凝土逐渐退出工作。此时。梁底部的拉应力由受拉钢筋与BFRP共同承担，特别是在跨中，BFRP的应力突然增大，与试验结论相一致。梁底部纵向纤维应力分布，见图9。

图8 开裂前纤维布应力

图9 开裂后纤维布应力

4 结论

FRP加固梁的破坏形态可以利用有限元软件ANSYS进行分析，对于加载时的荷载效应基本与试验结果吻合，能够为实际工程提供参考。但是在求解过程中，网格划分及荷载的确定都会影响求解是否收敛。同时，是否开启大变形选项是影响求解结果能否收敛的关键。所谓大变形，是指在非线性计算中随着混凝土的开裂及钢筋屈服等逐渐更新刚度矩阵，再逐步进行迭代计算。

[1]欧阳利军，丁斌，陆洲导.玄武岩纤维及其在建筑结构加固中的应用研究进展[J].复合材料，2010（3）：84-88.

[2]吴刚，胡显奇，蒋剑彪等.玄武岩纤维及其增强混凝土力学性能研究与应用.第十一届全国纤维混凝土学术会议论文集[C].大连：大连理工大学出版社.2006.9.

[3]戴光姣，黄亮.CFRP约束受压区混凝土梁抗弯性能试验研究[J].结构工程师，2016,32(1):133-138.

[4]赵志平，常建立，杨晓光等.利用ANSYS对碳纤维布加固RC梁的非线性有限元分析[J].四川建筑科学究.2006:32(1)：79-83.

[5]R.Z.Al-Rousan.Effect of CFRP Schemes on the Flexural Behavior of RC Beams Modeled by Using a Nonlinear Finite-element Analysis[J].Mechanics of Composite Materials,2015,51(4):437-446.

[6]蔺建廷.BFRP加固钢筋混凝土梁抗弯性能的试验研究[D].大连:大连理工大学，2009.

[7]中华人民共和国国家标准GB50010-2012混凝土结构设计规范[S].北京：中国建筑工业出版社，2012.

[8]孙跃东，于述强，彭亚萍.混凝土结构设计原理[M].北京:科学出版社，2013.

Nonlinear Analysis of Beams Strengthened with FRP Based on ANSYS

CHENGGuang-fu,YANGYong-shan
（College ofCivil Engineeringand Architecture，ShandongUniversityofScience and Technology，Qingdao266590，Shandong)

Based on the finite element software ANSYS,with 3 basalt fiber(BFRP)reinforced beam test as the basis,through the selection of element type and convergence criterion,the fiber composite flexural performance of strengthened beam are analyzed by nonlinear analysis.The analysis results show that the finite element simulation software of strengthened beam destructive form is consistent with the actual test results,and can well simulate fiber composite beams in ultimate load effect in the process of strengthening the use of ANSYS (span load deflection curves,cracking load and limit load etc.).Experimental data and calculation error is less than 10%,providinga reference for practical engineering.

finite element；BFRP；nonlinear；reinforce

TU17

A

1671-5004（2017）04-0004-04

2017-06-07

湖南省教育厅科学研究课题“面齿轮传动特性与齿面修形方法研究”（项目编号：14B015）

程光福（1992-），男，山东泰安人，山东科技大学在读硕士，研究方向：建筑与土木工程；

杨永山（1993-），男，山东潍坊人，山东科技大学在读硕士，研究方向：建筑与土木工程。