结合小波分析和变分原理的雷达图像去噪模型

王 俊,杨成龙

(陆军军官学院,安徽 合肥 230031)

结合小波分析和变分原理的雷达图像去噪模型

王 俊,杨成龙

(陆军军官学院,安徽 合肥 230031)

针对雷达侦察图像受乘性噪声的干扰而严重影响后期的图像处理问题,提出一种结合小波分析和变分原理的图像去噪模型。该模型首先利用bior3.7小波将雷达侦察图像分解为一个低频子带和三个高频子带,然后用小波软阈值法滤除低频噪声,用改进的全变分模型滤除高频噪声,最后通过小波逆变换得到去噪后的图像。其中,改进的全变分模型是通过将原有全变分模型中的扩散系数和保真项系数进行改进后得到的。MATLAB仿真结果表明,提出的去噪模型和传统的去噪方法相比,峰值信噪比平均提高了近1.2dB,并且在有效去噪的同时很好地保留了雷达侦察图像的边缘信息。

雷达侦察图像; 图像去噪; 小波变换; 全变分模型; 峰值信噪比

杨成龙(1993-),男,硕士研究生。

军用雷达作为空中军事力量的一员,具有全天候、全天时、穿透力强等特点,在现代战争中的作用和地位日渐突出。雷达的功能很多,如气象侦察、地球资源勘查和战场监视等,其中,它在军事领域的应用价值主要体现在作战一方可以通过雷达的探测图像判断出敌方战机和导弹等武器装备的具体位置,从而精确对其进行打击和摧毁。不过实际上雷达得到的图像信号往往存在大量的杂波干扰,包括雷达内部产生的噪声信号、回波间的相干叠加以及雨雪天气产生的杂波等。这些干扰的存在使得我们无法高性能地检测并摧毁目标,因此必须先对雷达图像进行去噪处理。

目前,去除雷达侦察图像噪声的方法主要是对其进行滤波,比较典型的有[1]:均值滤波、Lee滤波、Gamma滤波和基于小波变换的滤波等。这些滤波方法都取得了一定的去噪效果,但去噪的同时往往会使图像的边缘细节信息损失较多,另外,小波变换容易产生哑铃效应,使图像变得模糊。基于偏微分方程理论的去噪模型,如全变分模型[2],它在去噪的同时能够较好地保护图像的纹理特征,但在处理图像平坦区域时会产生“阶梯效应”[3-4]。鉴于以上几种去噪方法的优缺点,本文提出一种结合小波分析和变分原理的图像去噪模型,并从主、客观两个方面对模型的去噪能力进行评价,数值结果表明本文模型的去噪效果明显优于以往的方法。

1 全变分模型和小波阈值去噪法

1.1 全变分模型

全变分模型是Rudin、Osher和Fatemi于1992年提出的。他们首次将整体变分引入到了图像去噪领域:设u为观测到的图像,Ω是R2中的有界开子集,则u的整体变分为

(1)

从而得到基于TV(u)的图像能量泛函

(2)

其中,λ为保真项系数。根据变分法原理,E(u)获得最小值的必要条件是满足Euler-Lagrange方程:

-·+λ(u-u0)=0

(3)

最后通过梯度下降法得到TV模型:

(4)

1.2 小波阈值去噪法

小波阈值去噪的基本思路为:1)对含噪图像进行小波变换,得到一组小波系数;2)选择一个合适的阈值门限,并将那些比阈值门限低的小波系数当作噪声予以去除,将那些比阈值门限高的小波系数当作图像信息予以保留;3)对处理后的小波系数进行重构,得到的估计信号就是去噪后的信号。其去噪过程如图1所示。

图1 小波去噪过程

小波阈值去噪法通常又分为硬阈值去噪法和软阈值去噪法,其中,硬阈值是将图像的小波系数的绝对值和阈值门限进行比较,小于阈值门限的点小波系数置为0,其余的不变,设阈值门限为T,则硬阈值公式如下:

(5)

软阈值与硬阈值不同之处是当图像小波系数大于或等于阈值门限时,小波系数值变为该点值与阈值的差,其公式如下:

(6)

2 小波域耦合全变分模型图像去噪方法

为了更好地发挥小波阈值法和全变分模型在去噪方面的优势,本文提出将二者结合用于对雷达侦察图像进行去噪,并将全变分模型中的扩散系数和保真项系数进行改进,以达到更好地去噪效果。

2.1 模型的建立

2.1.1 改进的阈值

(7)

其中,N为子带图像大小,M为总的分解尺度,m为当前分解尺度,σ为噪声标准方差。

2.1.2 改进的保真项系数

由式(4)可以看出,全变分模型中的λ是一个全局变量,而实际上图像不同部位的信噪比是不同的,去噪时始终用同一λ作为保真项系数显然是不合理的。众所周知,在图像处理过程中,所有图像最终都会受到人类视觉系统的观察和分析,这暗示我们在图像处理过程中应当考虑视觉心理与心理物理学的作用[7]。因此,本文根据人类视觉系统的结构化特性对λ进行改进:

首先,本文结合文献[7],将噪声可见度函数g(i,j)取为

(8)

其中,M(i,j)为噪声屏蔽函数,其计算式如下:

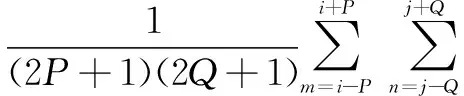
(9)

上式中,(2P+1)×(2Q+1)为关于点(i,j)对称的分析窗口的大小,mu(i,j)为局部均值,其计算式如下:

(10)

最后,本文利用噪声可见度函数将保真项系数取为

λ=e-g(i,j)

(11)

从式(8)、(11)可以看出:本文所取的λ可以自适应地调节正则项和保真项的比重:在图像边缘区域,对应的梯度|u|和噪声屏蔽函数M(i,j)都比较大,此时噪声可见度函数g(i,j)较小,λ的值越大,从而有利于保护图像的纹理信息;相反,在图像平坦区域,对应的梯度|u|和噪声屏蔽函数M(i,j)都比较小,此时噪声可见度函数g(i,j)较大,λ的值越小,从而有助于消除噪声。

2.2 模型的去噪流程

由于雷达侦察图像所含噪声为乘性噪声,这使得针对加性噪声的去噪模型(如全变分模型)不能直接用于处理这类含噪图像[8]。为此,本文通过先对其进行对数变换,然后再利用本文提出的模型对图像进行去噪处理,具体流程如图2所示。

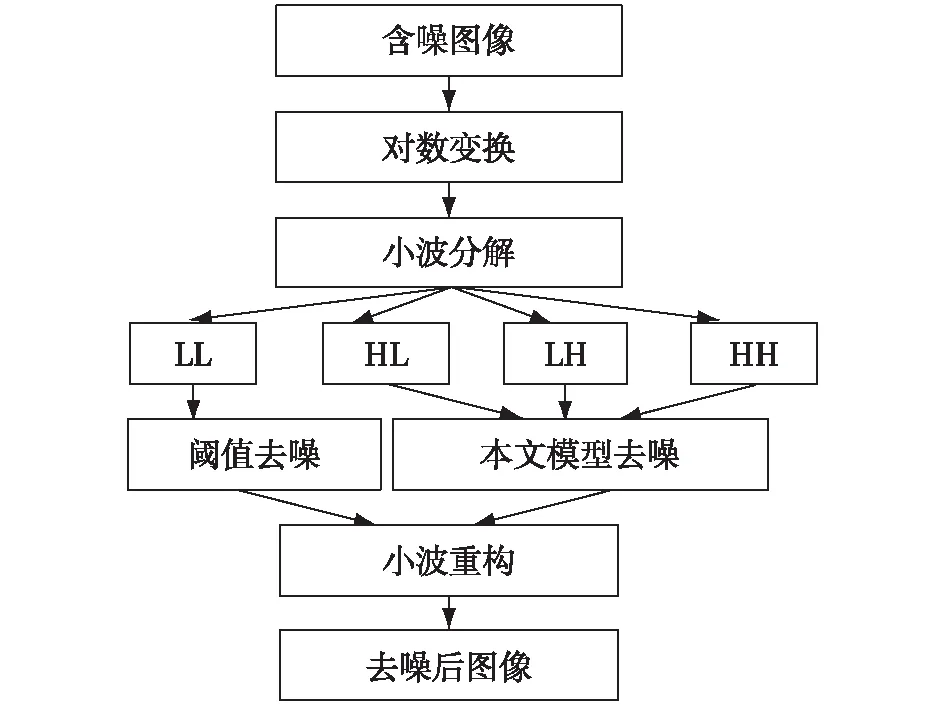
图2 本文模型的去噪流程

3 实例分析

在进行仿真实验前,必须先确定相关参数的值,如时间步长Δt,空间步长h,噪声方差σ2,阈值δ和保真项系数λ。通常我们在研究一个模型的去噪效果时,都是通过给干净的图像人为地加上噪声,因此噪声方差等数据一开始就知道。但本文的雷达侦察图像Rosenheim与一般的灰度测试图像不同,我们一开始并不知道噪声方差的大小,因此必须先对其进行估计。本文采用Donoho和Johnstone提出的利用含噪图像的小波变换系数来估计噪声方差,该方法可表示为:

(12)

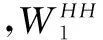
对于阈值δ,本文中子带图像大小N=255,总的分解尺度M=3,若当前分解尺度m=1时,根据式(7)可计算出阈值δ=0.077,此后阈值δ还会根据实验中的相关数据变化而变化。

最后再由式(8)-(11)计算出保真项系数λ=1.64,此后保真项系数λ也会根据实验中的相关数据变化而变化。

为验证本文方法的有效性,下面以一幅雷达侦察图像Rosenheim为例,并以峰值信噪比PSNR、均方根误差MSE和相对误差RelErr为评价指标,将本文模型与小波软阈值法和全变分模型进行比较实验。其中,图3为各模型对Rosenheim图像的去噪效果对比,表1为经各模型处理后Rosenheim图像的各性能参数。实验中时间步长Δt=0.1,空间步长h=1,噪声标准差σ、阈值δ和保真项系数λ的值为前面设定的值。

图3 各模型对Rosenheim图像的去噪效果

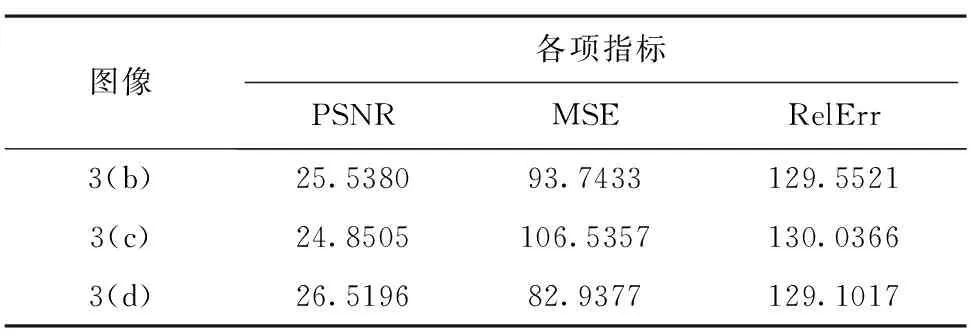
表1 去噪后Rosenheim图像的各性能参数

从图3可以看出,本文提出的去噪模型对雷达侦察图像具有较强的去噪能力,且比小波软阈值法和全变分模型的去噪效果要好,在去噪的同时还很好地保留了图像的边缘,使得去噪后的图像纹理细节更加清晰[9]。从表1的数据可以看出,一方面,和原雷达侦察图像相比,经本文模型去噪后的图像对应的PSNR都更大,MSE和RelErr都更小,说明本文模型达到了一定的去噪效果;另一方面,本文模型对应的PSNR最大、MSE和RelErr最小,说明其去噪效果最好。

4 结束语

本文从雷达侦察图像的几个重要特征出发,在小波分析和变分原理的基础上,通过对小波的阈值以及全变分模型中的保真项系数进行改进，提出一种小波域耦合全变分模型的图像去噪模型。该模型较好克服了小波阈值去噪法和全变分模型在去噪方面的不足,既能有效滤除噪声,又能使图像的细节特征得到很好的保留,并且从各项实验数据看,本文模型在雷达侦察图像去噪方面有着一定的优势,因此本文模型是一个较好的图像去噪模型。

[1] 周涛,周钰鑫.基于全去斜率接收技术的雷达距离成像[J].指挥控制与仿真,2017,39(1):83-88.

[2] Rudinl L,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].PhysiscaD:Nonlinear Phenomena,1992,60(1):259-268.

[3] 张长胜,冯广,刘子裕,等.改进各向异性扩散模型在图像滤波去噪中的应用[J].传感器与微系统,2017,36(4):157-160.

[4] 陈龙,蔡光程.基于PDE的图像去噪方法[J].计算机工程与应用,2015,51(16):142-145.

[5] 李艺珠,沈汀.非下采样小波域的四阶偏微分SAR图像去噪[J].遥感信息,2016,31(6):95-99.

[6] 王利娜,何文章,李长领，等.基于小波变换和ROF模型的图像去噪算法[J].天津职业技术师范大学学报,2015,25(2):39-42.

[7] 陈一虎,叶正麟.一种改进的各向异性扩散图像去噪方法[J].计算机工程与应用,2008,44(13):170-172.

[8] 黄义,马乐梅,解维河.测速雷达在舰炮试射中的应用方法[J].指挥控制与仿真,2015，37(5):118-120.

[9] 王相海,李放,王爽.小波方向子带偏微分方程遥感图像去噪[J].中国图象图形学报,2012,17(5):721-728.

Radar Image Denoising Model Based on Wavelet Analysis and Variation Principle

WANG Jun,YANG Cheng-long

(Army Officer Academy,Hefei 230031,China)

Aiming at the problem of the radar reconnaissance image processing in the later stage was heavily influenced by the multiplicative noise,an image denoising mode based on wavelet analysis and variation principle was proposed.First of all,the model decompose the radar reconnaissance image into a low frequency band and three high-frequency band by using bior3.7 wavelet,then use the wavelet soft threshold method to filter the low frequency noise,and use the the improved total variation model to filter the high frequency noise.Finally,the image is obtained by the wavelet inversion.Among them,The improved total variation model is obtained by improving the diffusion coefficient and the fidelity coefficient of the original total variation model.MATLAB simulation results show that the peak signal to noise ratio of the model in this paper has been increased nearly 1.2dB.Meanwhile,it can keep image edges and details very well.

radar reconnaissance image; image denoising; wavelet transform; total variation model; peak signal-to-noise ratio

TN957.52；E917

A

10.3969/j.issn.1673-3819.2017.05.009

1673-3819(2017)05-0041-04

2017-07-06

2017-07-13

王 俊(1965-),男,安徽无为人,博士,副教授,研究方向为偏微分方程及其数值解法以及偏微分方程在军事上的应用。