粒子群算法中惯性权重参数
王泽儒, 李芬田, 王红梅
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
粒子群算法中惯性权重参数
王泽儒, 李芬田, 王红梅*
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
研究粒子群算法惯性权重与种群规模大小、空间维度以及惯性权重递减率的关系,对多个具有代表性的函数进行实验研究。结果表明,适当改变惯性权重可以快速收敛、提高搜索效率以及避免陷入局部最优。
粒子群; 种群; 空间维度; 惯性权重; 递减率
0 引 言
粒子群算法[1-2]是一种进化仿生算法,1995年由Eberhart 和Kennedy[2-3]提出,源于对鸟群捕食的行为研究。粒子群算法是模拟群体智能所建立起来的一种优化算法,粒子群算法可以用鸟类在一个空间内随机觅食为例,所有的鸟都不知道食物具体的位置和方向,但是它们知道距离食物大约有多远,最简单快速的办法就是搜寻当前距离食物位置最近的鸟的周围区域。所以,粒子群算法就是把鸟看成一个个粒子,并且它们拥有位置和速度这两个属性,然后根据自身已经找到的离食物最近的解和参考整个共享于整个集群中找到的最近的解去改变自己的飞行方向,最后会发现,整个集群大致向同一个地方聚集。而这个地方是离食物最近的区域,条件好的话就会找到食物,这就是粒子群算法。粒子群算法相对于其他优化算法的优势在于容易实现,过程简单,并且没有很多参数需要调整。目前.粒子群算法已广泛应用于模糊系统控制[4]、函数优化[5]、电网规划和建筑结构损伤中的应用[6]、神经网络训练[7]、Web应用[8]、电路系统应用[9]、数据聚类[10]等。
目前阶段对于粒子群算法的研究主要集中在3个方面:
1)算法改进研究;
2)算法性能分析;
3)算法应用领域研究。
而对于算法性能分析研究主要集中在算法中各个参数的不同取值组合对算法性能的影响。在粒子群算法中,惯性权重是最重要的并且可以调整的参数之一。文献[11]指出,当惯性权重较大,算法的全局搜索能力较强,找到全局较优解的概率较大;反之,算法的局部搜索能力较强,收敛速度较快。若想平衡好全局搜索能力和局部搜索能力,惯性权重选取的方法是问题的关键所在。
文中研究了粒子群算法中惯性权重的选取与种群规模大小、空间维度与惯性权重递减率三者的关系。在迭代过程中,惯性权重是以线性递减率来线性递减,这种线性递减惯性权重称为可变惯性权重。这种可变惯性权重在每次迭代后提高了收敛速度,局部搜索能力越来越强。通过三个具有代表性函数进行实验研究表明,可变惯性权重具有很好的优化效率。
1 粒子群算法
1.1粒子算法一般框架[12]
假设存在一个D维空间的目标搜索空间,搜索空间中有m个粒子组成的一个种群,其中第i个粒子在D维搜索空间中的位置xi= (xi1,xi2,…,xid),第i维的飞行速度Vi= (vi1,vi2,…,vid),记第i个粒子的当前搜索到的最好位置为pi= (pi1,pi2,…,pid),整个粒子群目前在搜索空间中搜索到的最好的位置为g=(g1,g2,…,gd),则根据下式进行更新其速度和位置为

式中:c1,c2----学习因子,取值范围是非负数,通常取值为2;
r1,r2----[0,1]之间的随机数;
w----惯性权重,其大小决定了粒子对当前速度改变的大小,合适的选择可以提高粒子群算法的效率。粒子速度被限定在一个最大速度V_max的范围内。
算法过程如下:
1)设置种群规模为P_num,初始化粒子群,包括每个粒子的随机位置和速度;
2)重复下述操作,直到满足终止条件。
①计算每个粒子的适应值;
②根据粒子的适应值来更新粒子i的最好位置pi和粒子群的最好位置gfit;
a)如果该粒子的适应值比pi好,则将其作为当前的最好位置p;
b)如果该粒子的适应值比gfit好,则重新设置gfit。
③根据式(1)和式(2)改变粒子的速度和位置;
④输出粒子群的最好位置gfit。
1.2惯性权重
惯性权重是在粒子群算法中调整全局搜索与局部搜索中可控的重要参数。文献[13]指出,比较大的惯性权重有利于全局搜索,但是搜索效率低,算法开销较大;较小的惯性权重可以增加算法的收敛速度,但是很容易陷入局部最优。设置合理的惯性权重,可以避免陷入局部最优并且是高效搜索的关键。
在现实问题的背景下,惯性权重需要怎么去设置,要同时分析的因素有很多。其中,对当前搜索状态影响最大的参数是种群规模大小、搜索空间维度以及惯性权重递减率,这三者与粒子群算法惯性权重有着密切的关系。下面分别对种群规模、搜索空间维度以及惯性权重递减率进行分析。
种群规模的大小是决定粒子对搜索空间分散密集重要因素。当种群规模较大时,粒子分散较广,粒子所在区域覆盖较大,同时找到全局最优解的概率较大,应该减小惯性权重,提高局部搜索能力,以实现快速收敛与全局较优;种群规模较小时,特别对于多峰函数,粒子不能有效地分散在整个搜索空间,则应该增大惯性权重,提高全局搜索能力,避免陷入局部最优。
由文献[14]可知,当搜索空间维度较大时,粒子群算法常常收敛过早,很容易陷入局部最优。在复杂程度不同的问题背景下,搜索效率与寻优能力之间寻求较好平衡极为重要。对于高维度的搜索空间的复杂问题,应该通过减小惯性权重值的方法来提高全局搜索能力,尽可能地避免过早的收敛导致优化陷入局部最优。相反,当搜索空间维度较小时,应该增大惯性权重值实现快速收敛来提高效率。
通常,在全局优化算法中,我们总是希望在优化前期具有较好的全局搜索能力,以便快速地找到合适的优化点,而后在优化后期具有较好的局部搜索能力,以便来加快收敛的速度,所以,粒子群算法的惯性权重值应该是变化的,并且是递减的。
由以上分析可知,惯性权重与种群规模大小、搜索空间维度与惯性权重递减率有着密切关系,惯性权重的取值将会影响粒子群算法的优化效果。
1.3关于惯性权重的分析与实验
惯性权重作为粒子群算法中重要的参数,其主要分为两类:固定惯性权重和可变惯性权重。固定惯性权重就是选择某一个常数作为权重值,在优化的过程中权重值保持不变。而可变惯性权重就是选择某一个变化的范围,在迭代的过程中按照某一个线性递减率线性的减小,所以,可变惯性权重的选择包括变化的范围和递减率的选择。
测试函数见表1。

表1 测试函数
Rastrigin函数对优化算法具有很强的欺骗性,因为它有很多的局部最小值点和局部最大值点,很容易使算法陷入局部最优,而不能得到全局最优解。
Rastrigin函数图像如图1所示。
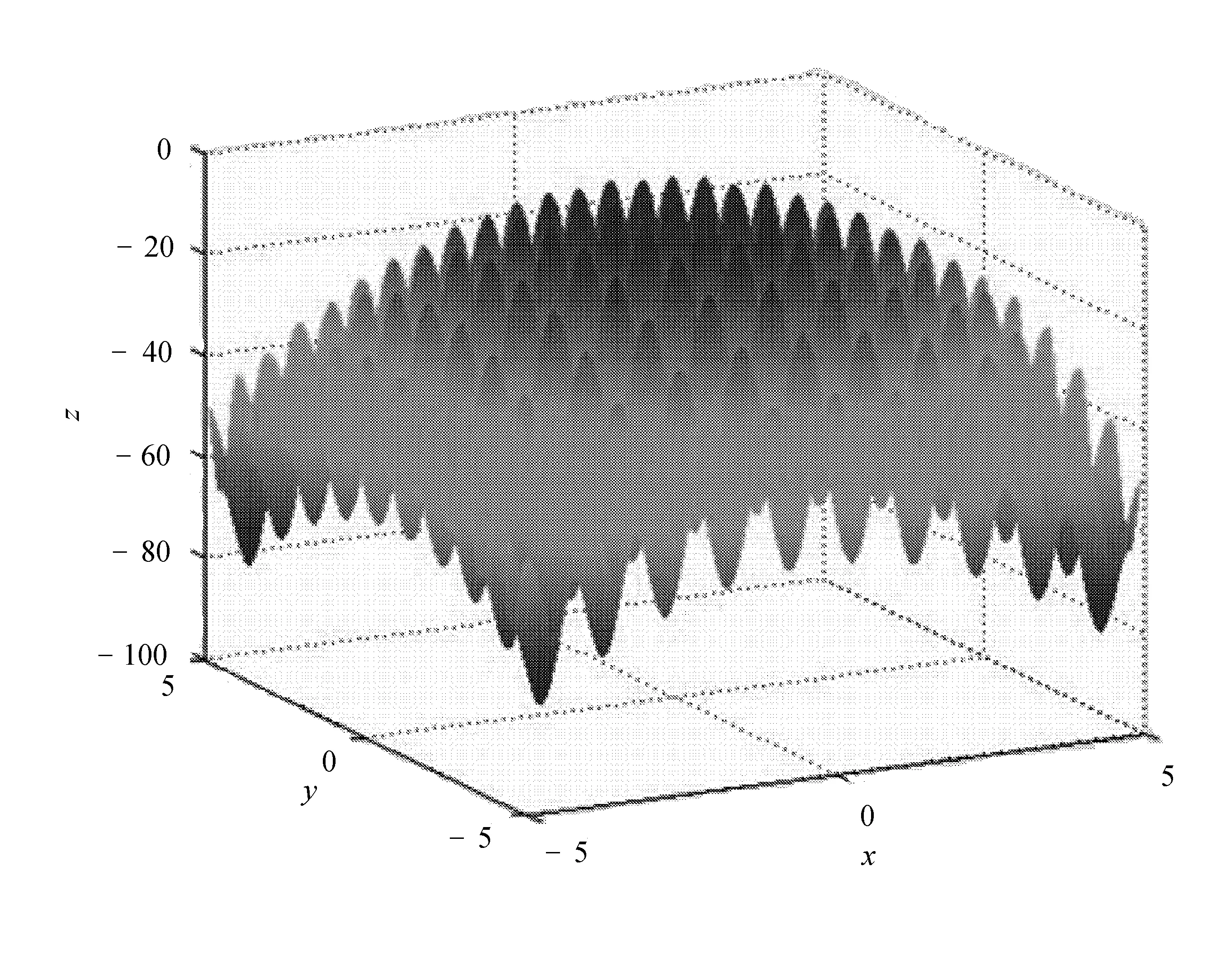
图1 Rastrigin函数图像
Rosenbrock函数图像如图2所示。
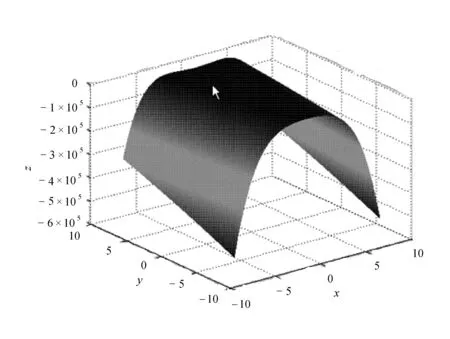
图2 Rosenbrock函数图像
测试环境如下:
操作系统:ubuntu 15.04×64;
编程软件:Code::Blocks。
电脑配置如下:
处理器:AMD A10-5745M APU with Radeon(tm) HD Graphics×4;
运存:4 GB。
程序设计:
文中测试代码使用C语言编写代码进行测试,主要的函数有main( ),initial( ),fitness(double a[]), renew_particle( ),renew_var( ),见表2。

表2 函数功能表
2 固定惯性权重和可变惯性权重选择
固定惯性权重使粒子始终具有相同的搜索能力,可变惯性权重使粒子在不同的时期具有不同的搜索能力,设置种群规模为30进行实验。
参数设置[14]如下:
1)w=0.6,c1=c2=1.7;
2)w=0.729,c1=c2=1.494;
3)可变惯性权重范围[0.2 - 0.9],递减率:(0.9-0.2)/4 000,c1=c2=2;
4)可变惯性权重范围[0.2 - 0.9],递减率:(0.9-0.2)/1 000,c1=c2=2。
在4个参数的设置下,进行20次优化测试函数实验,实验结果见表3。

表3 固定权重与时变权重在PSO中的表现
表3结果表明,文献推荐的惯性权重(包括学习因子)具有较好的收敛性,但是,可变惯性权重没有取得比惯性权重较好的效果。主要原因是文献推荐的惯性权重是经过实验详细的选择,而实验中的可变惯性权重只是简单的改变,调整递减率之后,收敛速度明显提升,说明经过精细的选择,将会有很大的进步空间。
3 可变惯性权重范围对收敛速度的影响
使用Rosenbrock函数对可变惯性权重范围及收敛速度的影响。参数设置种群规模为30,维度为30,每次运行最大迭代次数为4 000次,对函数进行优化20次,权重的变化率均定义为(w_max - w_min)/1 000,实验结果见表4。

表4 不同惯性权重变化范围对优化的影响
由表4可知,较小的惯性权重对Rosenbrock函数的影响比较大,有较强的优化效果,说明这个函数需要局部搜索的能力,即需要局部最优解。特别是在0.4~0.2这个范围内,全部达到了最优解。
递减率的选择应该考虑到对优化效果的影响,最好使平均迭代次数与递减率相匹配。通过表4可以看出,当惯性权重的范围在[0.4 -0.2]与[0.7 -0.2]之间优化比较好。现在继续选择Rosenbrock函数做实验,参数设置种群规模为30,维度大小设置为30,每次运行最大迭代次数为4 000次,对函数进行优化20次,改变可变惯性权重的递减率,实验结果见表5。
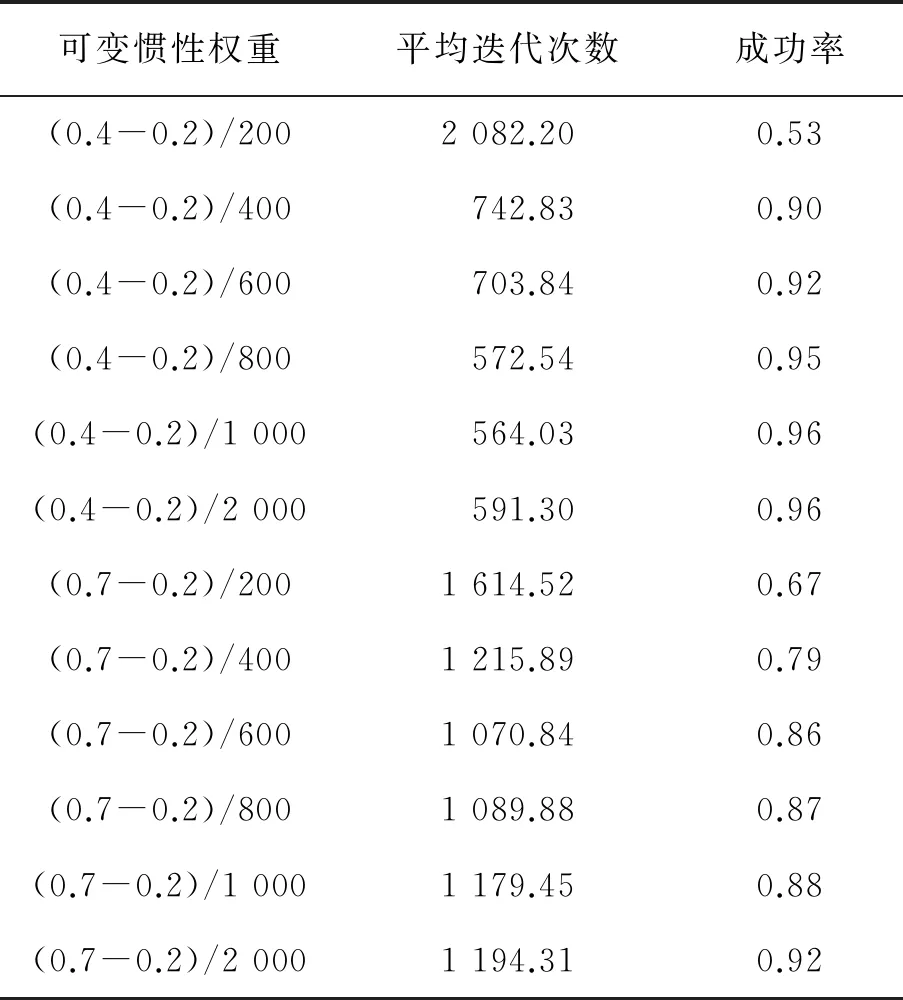
表5 不同递减率的可变惯性权重优化效果
从表5可以看出,在同一个变化范围内,随着递减率的减少,优化的成功率增加。说明在种群规模覆盖率较大的情况下,需要提高局部搜索能力,以达到快速收敛的目的。
4 惯性权重选择的问题依赖性
从前面的实验可以得出结论,Rosenbrock函数在使用可变惯性权重递减率(0.4-0.2)/2 000能取得较好的优化效果。对其他函数是否如此,这里我们做个实验,设置维数均为30,参数设置:权重的变化率均定义为(w_max-w_min)/1 000。实验结果见表6。

表6 Rastrigin函数与Sphere函数的优化效果
由上述实验可得,当可变惯性权重的递减率取值在(0.4-0.2)/1 000都可以有很好的优化效果。这说明惯性权重的取值对于问题有一定的依赖性,但不是很强。当可变惯性权重递减率在(0.7-0.2)/1 000的时候,测试函数对于优化效果都比较满意。
5 种群大小对于惯性权重选择的影响
增大种群,将会增加算法并行性,但是种群增大并不意味着惯性权重的选择重要,由上述实验可以得出,当可变惯性权重递减率在(0.7-0.2)/1 000的时候,测试函数对于优化效果都比较满意。我们改变粒子的数目为60,100进行实验,实验结果见表7和表8。
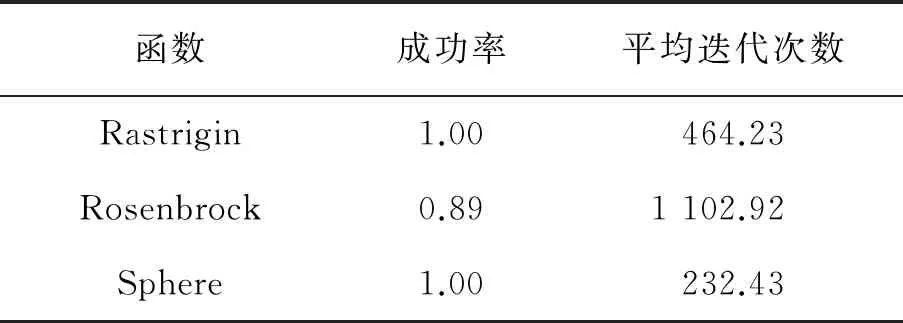
表7可变惯性权重(0.7-0.2)/1 000下增加粒子数目为60对优化效果的影响

表8 可变惯性权重(0.7-0.2)/1 000下增加粒子数目为100对优化效果的影响
通过表6、表7和表8可以看出,增加粒子的数目可以改善优化效果,在已经达到最优效果的函数,增加粒子数目对迭代次数并没有很明显的改变,所以应当调整惯性权重。
经过实验和选择,当惯性权重变为(0.375-0.2)/1 000所有函数将取得最优值,现在我们将惯性权重改变为(0.375-0.2)/1 000进行实验,实验结果见表9。

表9 可变惯性权重(0.375-0.2)/1 000下规模为100的优化效果的影响
由表9可以看出,当增加种群规模的时候,相对减小递减率的取值范围,可以取得较好的优化,这是因为当增大种群规模的时候,粒子更加专注自己身边小范围的搜索,对于发展能力增强,全局搜索能力减弱。
6 结 语
综上所述,在粒子群算法中,惯性权重的选择是一个重要的问题,适当的选择将会提高优化效率,同时,惯性权重对于问题的依赖不大,经过详细的选择,很多问题都可以在相同的可变惯性权重下取得比较好的优化效果。随着种群规模大小的增大,粒子更加注重于自己身边小范围的搜索,所以应当适当的减少惯性权重的值。随着搜索空间维度的增大,应该减小惯性权重值以提高全局搜索能力,避免过早收敛而陷入局部最优。相反,当搜索空间维度较小时,为提高搜索效率,应该增大惯性权重值实现快速收敛。在一般的全局优化中,前期有较高的全局搜索能力以找到合适的优化点,惯性权重值应该较大,而后期具有较高的局部搜索能力,以加快收敛速度,所以惯性权重值应该是递减的。
[1] Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE lnt. Conf. on Neural Networks, Piscataway: IEEE Service Center,1995:1942-1948.
[2] Eberhart R, Kennedy J. A new optimizer using particle swarm theory[C]//Proc. on lnt. Symposium on Micro Machine and Human Science, Piscataway: IEEE Service Center,1995:39-43.
[3] 刘志雄,梁华.粒子群算法中随机数参数的设置与实验分析[J].控制理论与应用,2010,27(11):1489-1496.
[4] 李维嘉,兰秋华,彭勇,等.基于粒子群算法的滑阀节流槽优化设计[J].中国机械工程,2015,26(8):995-999.
[5] 王建林,吴佳欢,张超然,等.基于自适应进化学习的约束多目标粒子群优化算法[J].控制与决策,2014(10):1765-1770.
[6] 丁帅伟,姜汉桥,周代余,等.基于改进粒子群算法的不规则井网自动优化[J].中国海上油气,2016,28(1):80-85.
[7] 吕雪冬.基于粒子群优化BP神经网络在电站锅炉中的应用研究[D].合肥:安徽大学,2015.
[8] 温涛,盛国军,郭权,等.基于改进粒子群算法的Web服务组合[J].计算机学报,2013,36(5):1031-1046.
[9] 杨丽华.粒子群算法在电力系统中的应用研究[J].科技与创新,2016(3):90-90.
[10] 王金永,董玉臣.改进料子群算法在数据聚类中应用[J].长春工业大学学报,2015,36(6):664-672.
[11] 黄珍,潘颖,曹晓丽.粒子群算法的基本理论及其改进研究[J].硅谷,2014,7(5):37-39.
[12] 皮倩瑛,叶洪涛. 一种动态调节惯性权重的粒子群算法[J].广西科技大学学报,2016,27(3):26-32.
[13] 黄太安,生佳根,徐红洋,等.一种改进的简化粒子群算法[J].计算机仿真,2013,30(2):327-330.
[14] 李聪,宋文龙.一种基于适应值分析的智能粒子群算法[J].计算机与现代化,2015(5):21-24.
Inertiaweightparametersinparticleswarmalgorithm
WANG Zeru, LI Fentian, WANG Hongmei*
(School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012, China)
The relationship between Inertial weight parameters with population size, space dimension and decreasing rate of the inertia weight are studied for particle swarm algorithm. Experiments are made based on some typical functions. The results show that inertia weight variation can let the algorithm quickly converged, searching efficiently and local optimization avoided.
particle swarm; population size; space dimensions; inertia weight; decreasing rate.
TP 301
A
1674-1374(2017)04-0354-07
2017-03-21
吉林省科技厅发展计划基金资助项目(20160415013JH)
王泽儒(1992-),男,汉族,山东临沂人,长春工业大学硕士研究生,主要从事数据挖掘技术方向研究,E-mail:rrwangzeru@163.com. *通讯作者:王红梅(1968-),女,汉族,吉林长春人,长春工业大学教授,博士,主要从事数据挖掘技术方向研究,E-mail:wanghm@ccut.edu.cn.
10.15923/j.cnki.cn22-1382/t.2017.4.07

