基于未知输入观测器的悬架故障诊断
张袅娜, 付留杰, 徐才茂, 周长哲
(长春工业大学 电气与电子工程学院, 吉林 长春 130012)
基于未知输入观测器的悬架故障诊断
张袅娜, 付留杰, 徐才茂, 周长哲
(长春工业大学 电气与电子工程学院, 吉林 长春 130012)
首先将故障作为观测器的未知输入,从而通过观测器的设计来解耦故障与系统状态,然后用公式来统一描述悬架系统执行器故障、传感器故障以及元器件故障。Simulink仿真实验验证了观测器的可行性。
汽车悬架; 故障诊断; 未知输入观测器
0 引 言
随着汽车的普及,人们的出行越来越依赖于汽车。我国道路交通条件经过多年的发展越来越完善,高速公路近年来发展迅速,让汽车行驶越来越快成为了可能。与此同时,人们生活质量也越来越高,这都要求驾驶汽车时更易操控,乘坐时更舒适。我们乘坐汽车时的舒适度与汽车的悬架系统密不可分,安全性也与之有关,因此,对悬架定期进行维护和检修,并进行故障诊断,是汽车悬架更平稳工作的保障,悬架的工作状况对汽车动力性的发挥更是重要。由于悬架系统存在的干扰是无法测量的,所以文中采用基于未知输入的观测器来实现悬架系统的故障诊断[1-3]。
在1970年前后,人们才开始对未知输入观测给予关注,并迅速展开了研究。对于线性系统以及非线性系统的研究成果也很多。文献[4]针对线性系统存在的未知输入提出了全维未知输入观测器的直接设计方法,该方法通过选择恰当的矩阵使观测器中不存在未知输入。对于线性系统中的可测干扰以及未知输入,文献[5]通过选择恰当的观测器增益处理了这个问题,进而提出了降维观测器的设计思路。在不确定系统中,未知输入或输出干扰是让人头疼的问题,文献[6]采用鲁棒H∞滑模来设计观测器,提出了估计状态和重构未知输入方法。文献[7]提出了两种方法对液压伺服系统研究故障诊断,这两种方法是小波神经网络方法以及专家系统方法,对于该方法,精确的系统模型是不需要的,但实际数据却是越多越好,而且是必须的,这使得该方法在实际的应用中受限。
为了在现实中有用武之地,以汽车的悬架为模型进行研究,针对其含有的未知输入进行了未知输入观测器 (Unknown Input Observer, UIO)的设计,提出了一种能统一描述系统执行器故障、元器件故障以及传感器故障的方法,进而实现对系统的故障诊断[8-9]。通过对汽车悬架模型的仿真,可知该方法是可行的。
1 UIO故障诊断原理及设计方法
对于典型的带有加性(Additive)未知输入项的线性时不变动态系统,其状态空间方程可表示为
其状态向量x(t)∈Rn,控制向量u(t)∈Rm,输出向量y(t)∈Rp,Gξ(t)为未知输入项。A、B、C、G为相应维数的确定系数矩阵。
根据未知输入观测器的设计思想,文中把故障信号当作系统的未知输入,设计如下形式的全维观测器
式中:z----全维观测器中的状态矢量,z∈Rn;
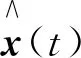
F、T、K、H为满足将未知输入从原系统状态估计误差中完全解耦的要求对应的维数矩阵。
由文献[10]知道,如果式(2)是式(1)所描述系统的未知输入观测器,那么其充要条件是[10]:
1)rank(CG)=rank(G);
2)(C,A1)可检测,其中
A1=A-G[(CG)T(CG)]-1(CG)TCA
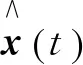
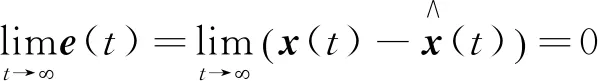
式中:e(t)----观测器的重构误差矢量。
联立式(1)~式(3),并令K=K1+K2,其中K、K1、K2∈Rn×p,可得
若使状态误差e(t)趋于零,进而完成全维的未知输入观测器设计,则需要满足下列条件[11]:
1)F具有全部稳定的特征值;
2)(HC-I)G=0;
3)T=I-HC;
4)F=A-HCA-K1C;
5)K2=FH。
则式(4)变为
因此,在进行未知输入观测器的设计时,首先要查看描述的模型是否满足未知输入观测器的充要条件;然后才能求解观测器(2)的矩阵F、T、K、H。其大致步骤如下:
1)判断是否满足rank(CG)=rank(G),如果满足,则继续下一步,否则退出。
2)判定(C,A1)的可检测性,即可观性。
3)假设(C,A1)可检测,则可直接给出矩阵F的期望特征值,接下来使用极点配置方法和对偶定理选择增益矩阵K1使F稳定,相继求出F、T、K、H,其中,H可取其特解,如H*=G[(CG)T(CG)]-1(CG)T;
4)如果(C,A1)不可观测,则必须用能观标准型对其进行分解,也就是说需要构造变换矩阵P来进行分解
A11∈Rn1×n1
C*∈Rm×n1
其中,n1为(C,A1)的能观型矩阵的秩,且(C*A11)是能观型矩阵。如果A22具有全部稳定的特征值,那么就可以知道矩阵(C,A1)能观测且能够使矩阵F稳定:
F=A1K1C=P-1[PAP-1-PK1CP-1]P=
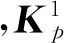
2 悬架系统建模及故障检测
2.1模型建立
汽车悬架是由不同的弹性和刚性原件组成,在未考虑故障的情况下,它是带有未知输入项的动态非线性系统,且该系统是典型的,该系统有较高的阶次,文献[11]归纳出了多种悬架模型。
文中采用的是在考虑非弹簧质量情况下的两自由度的1/4车体模型,如图1所示。
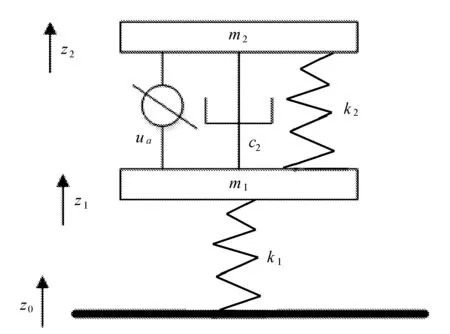
图1 汽车悬架车体模型
对于图1展示的悬架系统,其运动方程为
式中:m1----弹簧质量(也指车轮质量);
m2----非弹簧质量(即 1/4 车体质量);
z0----路面激励造成的垂直位移;
z1----车轮垂直位移;
z2----车体垂直位移;
k1----车轮弹性系数;
k2----车体悬架弹簧的弹性系数;
c2----减震器的阻尼系数;
ua----悬架系统的输入。
选取状态:
x1=z2-z1
x3=z1-z0
则系统模型为
式中:
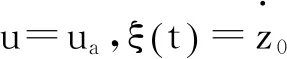
在考虑故障时,悬架系统的数学模型最终可化为如下形式:
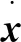

式中:IA----悬架系统中的元器件故障用元器件故障标识矩阵;
fi(t)----执行器故障;
f0(t)----传感器故障用向量。
而且这3个故障向量都是有界的。为了不失一般性,把上面建立的悬架模型式(11)进行拓展,以便使我们研究的故障诊断方法能够适用于大多数情况,假定x∈Rn,y∈Rp,u∈Rm,A0、B0、C0、D0、E0、G0、IA、ΔAa为相应维数的矩阵。
由于我们把故障视为系统的未知输入来进行分析,因此有对于线性向量函数f0(t)∈Rr和稳定的矩阵Af∈Rr×r,总存在一个向量α(t)∈Rr,使得下式成立[10]:
文中对于式(11)描述的系统,式(12)中的f0(t)相当于传感器故障向量。如果悬架系统包含p个测量信号,即y∈Rp,为了方便下文的研究,对传感器故障向量进行恰当的合并,使传感器故障向量的维数为r,且假设r 2.2故障检测 由于式(11)所示系统发生故障的表示形式存在不确定性,如果针对不同的故障形式设计故障检测方法,则存在冗余和故障检测不及时等缺陷,因此,用一种统一的故障表示形式来描述控制系统的故障模型是十分必要的。 对于含有干扰以及故障的悬架系统(11),文中使用单一的故障向量,即可描述系统状态方程,设计形式如下: 式中:x(t)∈Rn+r; u(t)∈Rm; y(t)∈Rp+r; A、B、C、D----响应维数的矩阵。 下面给出证明: 证明:对于式(11)描述的悬架系统,同时结合式(12),将式(11)和式(12)进行合并,可得到下列n+r阶的动态系统 定义新矩阵 则带有故障和干扰的悬架系统(11)可写成下式: 考虑系统 S(k)=A(eAT-I)-1(x(k+1)-eATx(k)) 下面给出证明: 证明:系统在(k+1)T时刻的状态为 从上面的证明可知,能够获知未知输入的估计值,这些未知输入包括加性未知干扰ξ(t),元器件故障ΔAax,以及执行器故障fi(t),从而诊断出执行器故障和元器件故障。 由于悬架系统的复杂性,文中为了更好地进行故障诊断,只考虑系统在执行器故障fi(t)、传感器故障f0(t)以及未知干扰下的故障诊断。因此,采用的模型为: 式中: D0=B0 α(t)∈R1 将式(21)和式(22)合并整理成式(14)、式(15)的形式,即 在仿真中,我们选取的悬架系统的参数见表1。 表1 仿真系数 则 依据UIO设计步骤,可以得到rank(CG)=rank(G),由公式A1=A-G[(CG)TCG]-1(CG)TCA计算出矩阵A1为 由公式H*=G[(CG)T(CG)]-1(CG)T和T=I-HC,可得到矩阵H和T为 从而,可求得F、K2、K为: 根据UIO结构和以上计算数据,在Matlab/Simulink中搭建用于对系统进行故障诊断的观测器。通过调整参数得到仿真结果分别如图2~图5所示。 图2 系统附加状态的实际值和观测值 图3 无故障时对附加状态ξ(t)的观测误差 图4 有故障时对附加状态ξ(t)的观测误差 图5 故障情况下的输出故障 从图2可以看出,系统的状态可以通过构造的观测器很好地观测到。 由图3可知,在无故障时,观测器对附加状态ξ(t)的观测误差在4 s之后接近于零。 由图4可知,在发生故障时,观测器也能够很好地观测到系统的状态,并在4 s时接近于零。 从图5可以看出,传感器发生故障时,文中设计的观测器能够观测出在满足未知输入观测器条件下的故障。 在研究汽车悬架系统的故障诊断中,从残差的生成和评价两方面入手,使用基于定性模型及定量模型相结合的方法,采用一种统一描述方法来表示系统传感器故障以及执行器故障,然后完成对未知输入观测器的设计,实现对悬架系统进行故障诊断。在观测器的设计中,将故障作为其未知输入,通过构造观测器,完成了对故障与状态的解耦。通过Matlab/Simulink仿真结果可以看出,文中所设计的UIO能够很好地对悬架的状态和故障进行观测,从而保证悬架工作在良好的状态。 [1] 柴天,韩旭,丁飞.量纲一化的悬架参数设计及评价方法[J].中国机械工程,2016,27(21):2939-2943. [2] 周东华,刘洋,何潇.闭环系统故障诊断技术综述[J].自动化学报,2013,39(11):1933- 1943. [3] 朱芳来,张永军.一种迭代未知输入观测器设计[J].同济大学学报:自然科学版,2014,42(8):1251-1255. [4] Yang F Y, Wilde R W. Observer for linear systems with unknown inputs[J]. IEEE Transactions on Automatic Control,1988,33(7):716. [5] Yang J, Zhu F. State estimate and estimation and simultaneous unknown input and measurement noise reconstruction based on associated observers[J]. International Journal of Adaptive Control and Signal Processing,2013,27(10):846. [6] Lee D J, Park Y S. Robust H∞sliding mode descriptor observer for fault and discrete time descriptor system[J]. IEEE Transaction on Automatic Control,2012,57(11):2928. [7] Li Guo you, Dong Min. A wavelet and Neural Net-works based on fault diagnosis for HAGC system of strip rolling mill[J]. Journal of Iron and Steel Research International,2011,18(1):31-35. [8] 胡志坤,孙岩,姜斌.一种基于最有未知输入观测器的故障诊断方法[J].自动化学报,2013,8(39):1225-1230. [9] 杨俊起,张良,朱芳来.Lipschitz非线性系统未知输入观测器设计[J].西安交通大学学报,2013,47(8):87-92. [10] 董敏,周彬.基于未知输入观测器的板带轧机液压压下系统故障诊断[J].中国机械工程,2013,24(20):2735-2740. [11] 管欣,张素民,詹军.基于凯恩方法的汽车悬架实时仿真模型[J].汽车工程,2010,32(8):649-653. Suspensionfaultdiagnosisbasedonunknowninputobserver ZHANG Niaona, FU Liujie, XU Caimao, ZHOU Changzhe (School of Electrical & Electronic Engineering, Changchun University of Technology, Changchun 130012, China) First, faults are regarded as the unknown inputof the observer (UIO) to decouple the faults and system states. Then, a formula is built to describe the actuatorfaults, component failures and sensor faults for the suspension system. Simulation verify the feasibility of the observation. utomobile suspension; fault diagnosis; unknown Input observer. TP 391.9 A 1674-1374(2017)04-0313-09 2017-04-17 国家自然科学基金青年项目(61603060); 吉林省发改委产业技术研究与开发专项(14Y126); 吉林省科技厅重点科技攻关项目(20160204056GX) 张袅娜(1972-),女,汉族,吉林长春人,长春工业大学教授,博士,主要从事汽车动态模拟与仿真方向研究,E-mail:zhangniaona@163.com. 10.15923/j.cnki.cn22-1382/t.2017.4.01

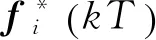
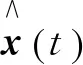
3 故障仿真研究






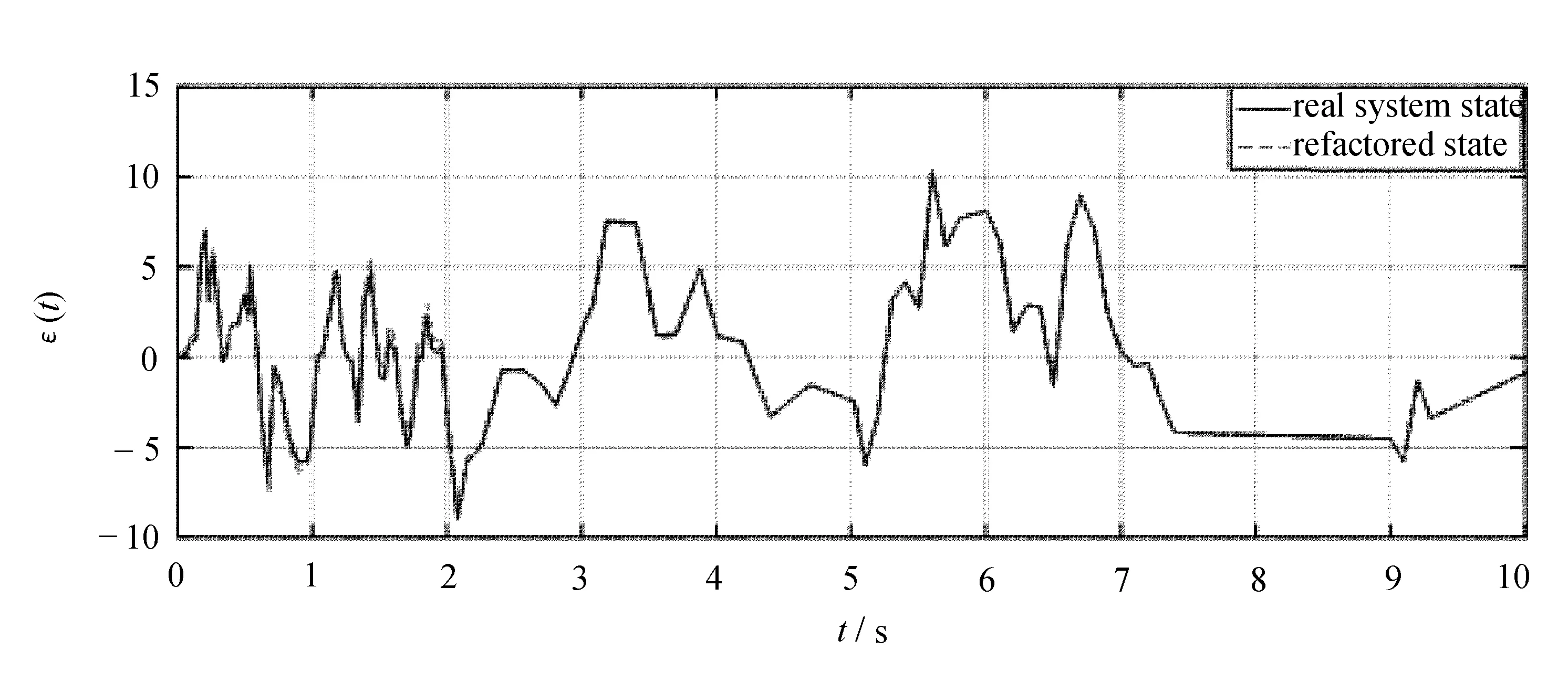
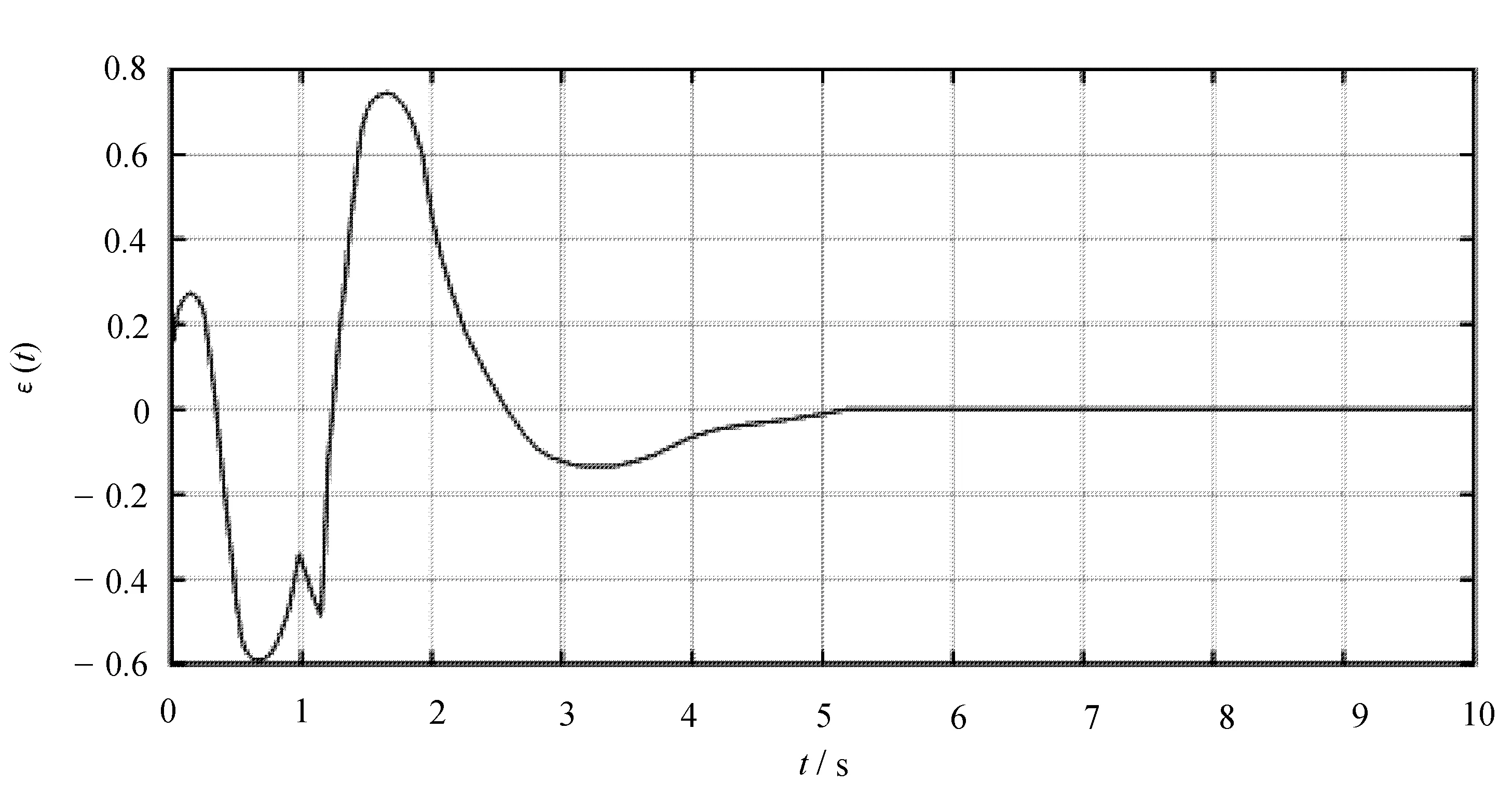

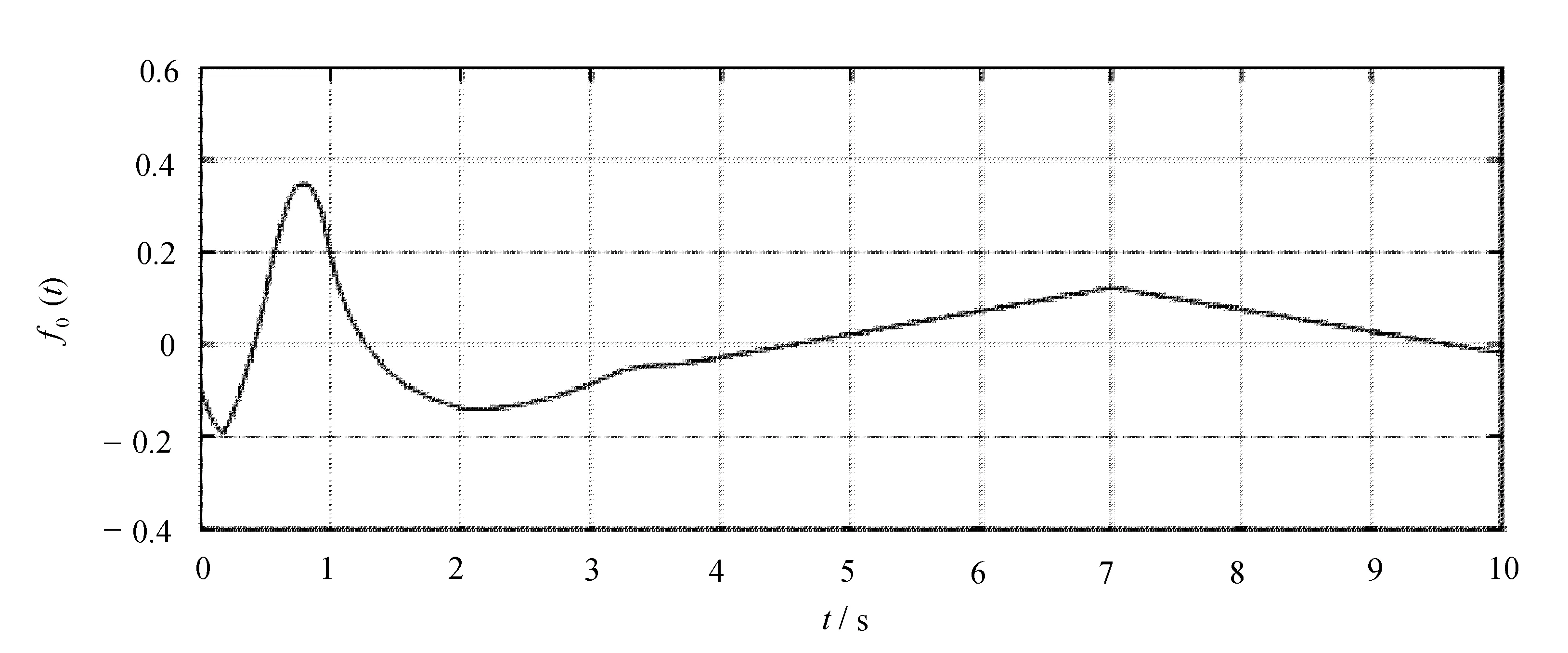
4 结 语

