底轴驱动翻板闸门动力特性数值分析

张维杰，严根华

（1.山东省水利科学研究院、山东水利岩土工程公司，山东 济南 250014；2.南京水利科学研究院，江苏 南京 210029）

底轴驱动翻板闸门动力特性数值分析

张维杰1，严根华2

（1.山东省水利科学研究院、山东水利岩土工程公司，山东 济南 250014；2.南京水利科学研究院，江苏 南京 210029）

以苏州河河口水闸工程底轴驱动翻板闸门为例，基于有限元分析方法和流固耦合理论，采用数值分析的方法，分别计算分析了无水、有水时闸门结构的自振频率和振型，并通过比较揭示了流体对底轴驱动翻板闸门动力特性分析的影响。

翻板闸门；动力特性；有限元分析；流固耦合

底轴驱动翻板闸门作为一种新型闸门结构，由于其具有门顶过水形成人工瀑布、启闭灵活可调、卧门行洪、双向挡水、无碍通航等特点，被广泛应用于城市河道管理中。在其运行过程中，闸门的静力特性一般满足要求，但受动水压力的影响，闸门结构常发生强烈振动，甚至导致结构动力失稳而破坏，造成重大事故。本文借助有限元分析软件ANSYS，研究了无水、有水时闸门结构的自振频率和振型，并通过比较揭示了流体对底轴驱动翻板闸门动力特性分析的影响。

1 结构动力平衡方程

处于流场中的结构与流体之间存在相互作用与相互影响，这种理论被称作流固耦合理论。对于闸门结构，其可进一步解释为：闸门在水体中运行时，在水动荷载作用下会产生振动，闸门的这种振动必然导致流场压力的波动，流场压力波动又进而影响闸门结构的振动，这是一个典型流固耦合振动问题。

分析结构的固有动力特性，最主要的就是求结构的自振频率及其对应的振型。结构在坐标系中离散化后的动力平衡方程为：

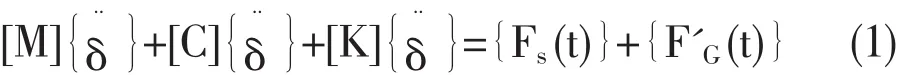
其中，[M]、[C]、[K]分别为结构的质量、阻尼和刚度矩阵；δ¨｛｝、δ.｛｝、｛｝δ 分别为结点的加速度、速度和位移；Fs(t｛｝)为结构耦合面上结点处的动水压力；｛FG(t)｝为结构上的其余作用力。

当考察结构的自由振动时，结构所受其余作用力｛FG(t)｝为0。与此同时，大量实例证明，结构的阻尼矩阵对结构自振频率和振型的影响极小，可忽略不计。简化后的动力平衡方程变为：

2 底轴驱动翻板闸门的动力特性分析

2.1 闸门结构布置

苏州河河口水闸工程底轴驱动翻板闸门主要部件包括：闸门门叶结构、底轴总成、拐臂部件、跨中和端部支铰。其中，闸门门叶为主纵梁结构，门叶总宽23.9 m，净高3.5 m，门叶沿高度方向设置5道水平次横梁和1道顶梁。

2.2 有限元模型

底轴驱动翻板闸门有限元模型的建立依次可分为几何模型、实体模型和有限元模型三步。为反应闸门受力情况，单元类型选择三维固体结构单元Solid185，网格划分方法采用四面体网格，单元大小根据闸门结构构件的位置、形状和尺寸分别设置，网格划分后形成的有限元模型如图1所示。其中，闸门共离散成531 426个单元，生成168 125个节点，门叶质量为68 273 kg。

2.3 边界条件的处理

在数值计算中，闸门门体设置为整体结构，可满足门体焊接的要求；底轴与门体接触部位通过粘结操作连接，刚度比螺栓连接大；施加边界约束的部位有吊耳环、底轴与支座接触部位，对上述两个边界作如下处理：1）拐臂与启闭机系统连接处的吊耳环直接采用刚接的方法，即约束了闸门的6个自由度，在一定程度上能模拟闸门全关时边界条件；2）闸门底轴与支座相接触的环面采用柱约束，释放环面切向的约束而保留环面轴向与径向约束，模拟底轴相对支座的转动。

图1 闸门结构有限元模型图（去除支座）

2.4 闸门干模态分析

闸门的干模态分析即不考虑水体作用，计算闸门本身的自振频率和振型。无水时，闸门的一、二阶振型如图2、图3所示。

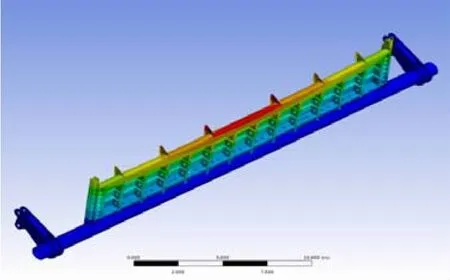
图2 闸门结构第一阶振型

图3 闸门结构第二阶振型

无水时，闸门前20阶自振频率范围为12.62~137.8 Hz，其中，从振型方面看，第2阶为门叶顶角扭转变形，第13、19阶为闸门门叶拉伸变形，第17、18、20阶为门叶弯扭变形，其余为闸门结构的弯曲变形，且多为多次弯曲变形；从振动发生的部位看，振动主要集中在闸门门叶，少部分为门叶和底轴整体变形。闸门结构的一阶振动频率为12.62 Hz，反映闸门门叶中上部的弯曲变形；闸门结构的二阶振动频率为19.04 Hz，反映闸门门叶两侧顶角的扭转变形。

2.5 闸门湿模态分析

分析闸门的湿模态特性需要建立闸门的流固耦合模型。其中，流体模型采用三维声学流体单元Fluid30划分，流体长度取10倍的闸门门叶高度25.00 m，沿长度方向将水体分为4部分进行网格划分，与闸门门叶接触部分网格尺寸最小，距离越远，网格尺寸越大。网格划分后，流固耦合模型共生成1 207 442个单元和277 954个结点，其中闸门结构生成494 345个单元，流体模型生成713 097个单元。翻板闸门流固耦合有限元模型如图4所示。流体—结构的耦合场分析采用直接耦合的方法，其余边界条件不变。

图4 闸门流固耦合有限元模型

有水时，闸门的前20阶自振频率范围为5.25~75.85 Hz。从振型方面看，第1阶振型反映闸门门叶的扭转变形，第3、8阶振型反映闸门的拉伸变形，第6、10、13阶振型反映闸门门叶的弯扭变形，其余均反映闸门的弯曲变形；从振动发生的部位看，大部分发生在门叶部位，只有第19阶为门叶和底轴的整体变形。底轴驱动翻板闸门有水时的一、二阶振型如图5~图6所示。

2.6 计算结果分析

由流固耦合理论可知，处于流场中的闸门与流体间存在相互作用，这种相互作用会影响闸门的自振频率和振型，在结构动力平衡方程中表现为附加质量矩。通过比较无水、有水时计算得到的闸门结构自振频率，可得如下主要结论：

1）有水与无水情况相比，底轴驱动翻板闸门的自振频率大幅度下降，频率降低百分比范围在40%～60%之间，其中下降较大的第1、7阶振动频率，下降百分比分别为58.40%和59.28%，降低最小的第17阶振动频率下降率也高达42.32%。

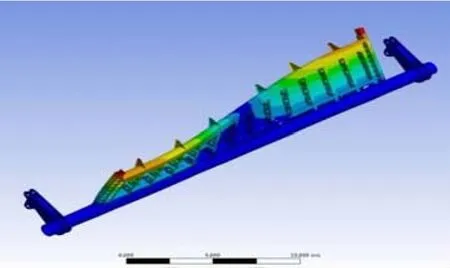
图5 闸门结构第一阶振型

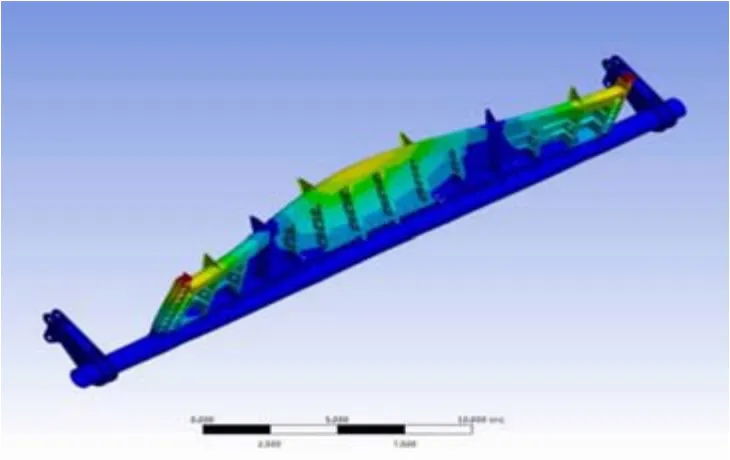
图6 闸门结构第二阶振型

2）与无水情况相比，有水时闸门的振型和振动部位发生了明显变化。无水时闸门的弯曲变形多为门叶和底轴整体变形，有水时闸门弯曲变形多发生在门叶部位。

3 结语

通过分析干、湿两种条件下闸门的动力特性，可以看出，门前水体不仅对底轴驱动翻板闸门的自振频率有较大影响，同时对闸门振型和振动发生部位也产生了显著影响。因此，在研究底轴驱动翻板闸门的动力特性时，必须考虑流体的影响，流固耦合效应不容忽视。

（责任编辑 崔春梅）

TV66

B

1009-6159（2017）-10-0064-02

张维杰（1990—），男，助理工程师