用数形结合之利 破问题研究之难——谈数学结合思想对小学生数学学习的帮助

□文/江苏省宝应县射阳湖小学 祁顺成

用数形结合之利 破问题研究之难
——谈数学结合思想对小学生数学学习的帮助

□文/江苏省宝应县射阳湖小学 祁顺成

数形结合思想是指把数量关系和空间形式之间有机融合的数学思想方法，即利用学生熟知且能够解读的几何图形，去简释问题之中的复杂关系或隐晦的联系，从而使以“形”悟“数”、用“数”解“形”得以最直观的呈现，也使得学生的数学学习如虎添翼。在小学数学教学中如能一以贯之地引导学生运用数形几何思想去研究问题、分析问题，势必能给学生最直观的感触，促进学习理解的深入，更好地刺激学生灵活运用形象表象等积淀去分析、思考和推理，让学生得到必要的思维训练，最终实现数学思维的飞速发展。

一、化抽象为直观，让关系更清晰

在小学数学教学中渗透数形结合思想不仅是我们的教学使命，也是我们发展学生良好数学素养的有效举措，更是发展学生思维、促进学习认知科学建构的基本路径。因此，我们应指导学生科学地绘制线段图、矩形图等示意图，给学生以直观的启迪，让习题的数量关系变得明了、清晰，从而使学生的数学学习变得愈加灵动，充满智慧。

如，三年级的一道数学题：“一箱苹果，连箱称一共重15千克，取出一半苹果后，连箱再称，这是重量是8千克。计算出苹果一共有多少千克？箱子重多少千克？”

对于一个三年级小孩来讲，苹果与箱子的关系就显得尤为抽象，特别是其中还有一个“一半”。所以引导学生尝试用图例来揭示问题中所蕴含的规律、把握习题的本质就显得十分重要了。

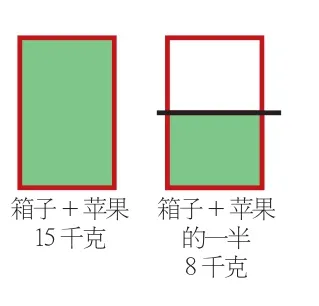
一方面组织学生解读习题，分析习题中所呈现的各种关系，能够明晰基本的逻辑顺序。另一方面引导学生尝试用图例表示出对应的数量关系，让学生利用图例揭示箱子、苹果之间的联系，把握准15千克、8千克的构成，找出蕴含在其中的变量与不变量。第三指导学生科学绘制示意图，在不同的学习成果展示活动中，我们能够找到一种既简洁，又便于解析的图例（见右图）。第四组织深度解读图例：生1：我发现箱子+苹果=15（千克），取出一半后变成箱子+苹果的一半=8（千克），从中看出箱子是不变的，苹果是变化的，而且只有原来的一半。生2：看图很明显，红色的箱子不变，绿色的苹果减少一半，我发现减少了15-8=7（千克），7千克就是苹果的一半，那么原来的苹果就是7千克的2倍，是14千克；这样15-14=1（千克），这就是箱子的重量。

从学生的学习来看，数形结合成为学生研究问题、分析问题、解决问题的有效拐杖。科学地引用数形结合策略，既能加速学习理解，又能发展学生的数学思维，让数学学习更具活力。

二、化繁杂为简洁，让思考更敏捷

小学数学解决问题中有很多的习题，其表述复杂，关系繁杂，从而导致学生解读困难，理解无所适从。因此，在小学数学教学中应灵活地引入数学结合策略，帮助学生解读繁琐，解析困惑，使得问题的关键点能够凸显出来，跃然纸上，让学生的数学学习产生意想不到的效果，收获理想的实效。

如，六年级有关百分数的一道习题：“有一种农药若干克，加入1杯水后，这时农药的含药率变为25%，再加1杯药粉后，农药的含药率是40%。请计算出原来农药的含药率。”

看完题目，很多同学都有很多的疑问：原来的农药有多少克啊？既加药粉又加水，其中有什么奥秘吗？是啊！含药率也在不断变化，一会儿是40%，一会儿是25%，怎么去分析其中的规律呢？引导学生进行解析，并学会用图例表示出对应的关系。把一份药粉表示为★，一份水表示为◆。根据“加入1杯水后，这时农药的含药率变为25%”，也可以表示为：★◆◆◆◆。根据“再加1杯药粉后，农药的含药率是40%”，可以表示为：★★◆◆◆；这样我们能够清楚地得知：1份药粉、1份水刚好也是1杯药粉、1杯水，如果没有加1杯水和1杯药粉这一变化，那么原来农药的含药粉则可以理解为：★★◆◆◆-★-◆=★◆◆，从土里可以得出，★就是★◆◆总和的1/3，所以原来农药含药粉率为33.33%。

从上述的图例我们能够感受到数形结合策略在研究问题、突破难点中的巨大优势，所以我们在教学中应不失时机、不遗余力灵活地渗透数形结合思想，以加速学习思考深入，促进数学思维的迅猛发展。

三、化隐晦为直白，让探索更便利

对于小学生来讲，读清问题的条件、理顺内在的关联、找准对应的关系等是解决问题的根本要素。然而，在小学数学诸多问题中，总有一些问题的条件隐藏得很深，导致题目晦涩难懂，成了学习研究的拦路虎。因此，指导学生学会用画图的策略来解密晦涩，使繁琐的关系逐渐清晰、明朗，从而提升学生的解题能力，加深学习感悟，积淀研究问题的经验。

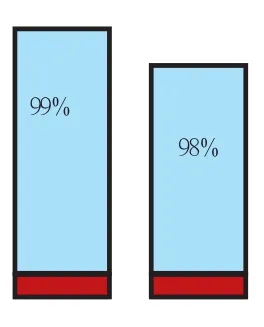
如，六年级一道百分数的问题：“有一种新鲜蔬菜若干千克，含水率是99%，经过晾晒后含水率变成了98%。这时蔬菜的质量是原来质量的百分之几？”

粗看题目，仅发现两个百分数存在，导致很多学生无法下手，从而使解题陷入尴尬的格局。然而，指导学生画图揭示其中的内在关系，我们就会发现晦涩关系的隐藏条件——蔬菜除了含水外，还有其他的物质，而这些物质无论怎么晾晒都不会变化的，找

出这个关键，也就使问题分析变得有章可循、有法可依了。因此，用画图策略使固定的那部分质量凸显出来。仔细观察图例，我们发现：红色的不变部分就是蔬菜的本质，而蓝色的部分（水分），是变化的。所以我们就可以设定红色部分的物质为a千克，那么原来的蔬菜总质量是a÷（1-99%）=100a（千克）；而当含水率变成98%时，蔬菜的本质部分还是a千克，这时蔬菜的总质量是a÷（1-98%）=50a（千克）；这样问题就很容易解决了，50a÷100a=50%。

从上面的图例中我们不难看出，只要画准示意图，并把握准对应的等量关系，问题就会迎刃而解，学习也会变得敏锐起来。巧用图形结合思想，不仅能促进学习的深入，加速学习思考的推进，更能突破学习难点，让数学学习充盈着智慧。

总之，在小学数学教学中我们应该科学地把握学生的知识积累现状、思维发展水平以及数学活动经验储备等诸多因素，科学地引入数形结合思想，让学生在画图中把握知识的真谛，寻觅到解决问题的良方，从而使数学学习充满灵性，闪烁着智慧的光芒。同时，也能有效地培养学生的数学思维，加速学习经验的积淀，使得学生的数学素养获得长足的发展。◇