基于VMD-SE和优化支持向量机的光伏预测方法

武小梅， 张 琦， 田明正

(广东工业大学 自动化学院，广东 广州 510006)

基于VMD-SE和优化支持向量机的光伏预测方法

武小梅， 张 琦， 田明正

(广东工业大学 自动化学院，广东 广州 510006)

针对光伏电站短期功率预测准确性的问题，提出了一种基于VMD-SE与改进的灰狼优化(Grey Wolf Optimization, GWO)算法优化支持向量机回归(Support Vector Regression，SVR)的组合预测方法。由于不同天气类型的光伏功率输出相差较大，因而利用相似日选取相同天气类型下的数据进行预测；考虑到光伏功率输出随机波动性较强，采用变分模态分解对原始光伏功率序列进行分解，以减少数据的非平稳性；为了克服支持向量回归参数盲目选取的弊端，利用改进的灰狼优化算法对其参数进行优化，以进一步提高数据的预测精度；最后，将分解后的子序列经样本熵重组后相加求和得到最终预测结果。算例结果表明，该组合预测方法整体上预测误差最小，有效提高了光伏输出功率预测的准确性，可以更好地保障电力系统的可靠运行。

光伏功率预测； 变分模态分解； 差分进化； 灰狼优化； 支持向量回归； 组合预测

0 引言

随着化石能源如煤、石油和天然气等越来越匮乏，太阳能作为丰富的、清洁的和可再生的能源，已成为绿色能源开发和利用的前景之一。因此，为了提高光伏系统的实时控制性能和减小可能产生的负面影响，光伏输出功率的准确预测是非常必要的[1]。

目前，光伏功率预测已提出了人工神经网络、马尔可夫链和机器学习[2-5]等诸多单一预测方法。但考虑到光伏功率受环境影响而呈现较大的不确定性，采用单一预测方法进行光伏功率预测将存在极大的误差，因此，组合预测模型得到了广泛的应用。文献[6]利用各单一模型的优势，根据某种权重关系筛选出最佳的权重系数，从而建立权重组合模型。文献[7]采用粒子群算法(Particle Swarm Optimization,PSO)优化BP神经网络的权值和阈值，但粒子群算法存在易陷入局部最优和后期收敛速度慢的缺点。文献[8]利用经验模态分解(Empirical Mode Decomposition，EMD) 的信号分解技术，通过将原始数据信号分解为不同尺度下的固有模态分量和剩余分量，并对各分量分别采用人工智能优化算法进行预测。但EMD分解的时间序列存在分模态混叠现象及端点效应。

因此，本文提出了一种新型的非递归、自适应分解技术—VMD分解，首先，将原始光伏数据序列通过VMD分解成有限带宽的子序列；为降低预测模型的复杂度，采用样本熵重组将各子序列重组分为趋势分量、细节分量以及随机分量；然后对各分量分别建立优化支持向量机回归的光伏功率预测模型。又考虑到支持向量机参数选取问题，利用具有良好全局搜索能力的改进的灰狼优化算法对支持向量机的学习参数进行优化，从而进一步提高预测模型的精度。最后，通过某光伏电站数据验证了该组合预测方法的有效性。

1 光伏功率预测模型

1.1VMD分解

变分模态分解(Variational Mode Decomposition，VMD)是一种新型多分辨率的信号分解技术，其整体求解过程即为变分问题的构造与求解。通过将光伏功率序列信号f分解为一系列具有中心频率ωk的有限带宽的子模态信号uk(t)，k=1,2,…,K为模态数量。其中，子信号uk的带宽具体构造步骤如下[9]：

(1)根据Hilbert变换，计算得到每一子模态uk相应的解析信号，从而求取其单侧频谱。

(2)通过对各模态解析信号对应的中心频率ωk的指数项e-jωkt混叠，将子模态信号uk的频谱变换至基频带。

(3)对上述解调信号梯度的平方L2范数进行计算，从而估计出子模态信号uk的带宽，其中带约束条件的变分问题为：

(1)

式中：{uk}={u1,u2,…,uk}、{ωk}={ω1,ω2,…,ωk}；δ(t)为狄拉克分布。

此外，变分问题的求解为：

(1)将式(1)带约束的变分问题通过二次惩罚因子α和拉格朗日乘子λ的引入转化为非约束的变分问题，可表示如下：

(2)

式中：α用于在高斯噪声存在时保证信号的重构精度；λ保持约束条件的严谨性。

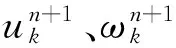
(3)对uk和ωk求解迭代的解为：

(3)

(4)

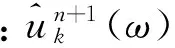
1.2样本熵

样本熵(Sample Entropy)是由Richman和Moornan[11]提出的一种新的度量时间序列复杂性的方法,是针对近似熵的改进算法，其目的在于降低近似熵的误差，与已知的随机部分有更加紧密的一致性。相比近似熵，样本熵具有不依赖于数据长度，是条件概率的负平均自然对数的精确值；并且样本熵具有更好的一致性特点，样本熵的值越大，序列越复杂，反之，表明序列的自相似程度越高。

1.3DE-GWO优化SVR

1.3.1 SVR原理

支持向量机(Support Vector Machines, SVM) 是于1955年由 Vapnik[12]等人提出的一种智能学习算法，具有较好的非线性处理能力和推广能力，尤其对高维数据处理时,能有效解决 “维数灾”问题。将SVM用于光伏功率预测的非线性回归预测问题，即可得到支持向量机回归SVR，SVR回归预测原理如下。

假设光伏功率预测样本数据为(xi,yi)，xi∈Rn,yi∈R,(i=1,2,...,l)，SVR的主要思想是利用非线性映射φ:Rn→Rm(m≥n)将原始数据映射到高维特征空间，然后根据方程f(x)=[ω·φ(x)]+b在该空间中线性回归。

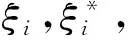
(5)

(6)

然后，根据Mercer原理，引入核函数K(xi,x)=φ(xi)·φ(x)，求解式(6)以得到决策回归函数为：

(7)

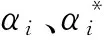
1.3.2 SVR参数优化

由于大量结果[13-14]表明核函数的选择对回归预测的准确率影响较小，而参数选择影响较大且采用核函数进行预测时，惩罚参数c和核参数γ对算法的表现起主导作用，当c值太大而γ值太小(0.1～1)时会使训练集出现过学习现象；当c值太小(0.1～10)而γ的值太大(100～10 000)时会使训练集出现欠学习现象。因此，本文采用DE-GWO算法优化SVR参数。

1.3.3 DE-GWO算法

灰狼优化(Grey Wolf Optimization, GWO)算法[15]是由Mirjalili等于2014年提出的一种新兴元启发式优化算法。它通过模仿灰狼群体跟踪、包围、追捕、攻击猎物等捕食行为实现优化的过程。相比其他进化算法，灰狼算法通过对比得到各灰狼社会等级并控制搜索方向，具有较高的优化效率、结构简单、参数设置少。由于篇幅原因，其算法的具体步骤及算法描述详见文献[16]。

由于GWO算法处理在高维优化问题时存在后期收敛速度慢、易陷入局部最优等问题。因而本文利用DE算法[17-18]优化GWO，将DE加入GWO中以更新灰狼当前最优位置的种群决策层中的α、β和σ，从而使GWO跳出局部最优。其算法具体步骤如下[19]：

Step1：定义DE-GWO相关参数。包括种群数目n，最大迭代次数τmax，决策变量Var，缩放因子M，交叉概率Pc。

Step2：根据式(8)随机初始化种群，其中X由SVR算法的学习参数C和γ构成：

(8)

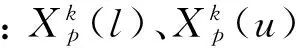
Step3：计算个体适应度值，并以非递减的顺序对个体适应度进行重新排序，确定适应度值排列前三位的灰狼个体位置Xα、Xβ和Xσ作为决策层。

Step4：根据式(9)更新灰狼父代种群中个体的位置，然后根据式(10)、(11) 进行变异、交叉操作，产生新的子代种群。

X(t+1)=Xp(t)-AD

(9)

Vi(τ)=Xr1(τ)+M·(Xr2(τ)-Xr3(τ))

(10)

(11)

式中：A为收敛因子；D为灰狼个体与猎物间的距离；M缩放因子；r1≠r2≠r3≠i；τ=0,1,2,…,τmax为迭代次数；CR为交叉概率；jrand为1到d之间的随机整数；d为个体数量的维数。

Step5：根据式(12)更新父代种群，再根据式(13)、(14)、(15)更新C、A和a。

(12)

C=2r2

(13)

A=2ar2-a

(14)

a(t)=2-2t/τmax

(15)

式中：k为种群数目；r2∈[0,1]间的随机数；C为摆动因子；a随迭代次数t增加而从2线性递减到0。

Step6：更新父代Pα、Pβ和Pσ，再以非递减顺序对灰狼父代群体重新排序。判断是否满足算法终止条件，若满足，则返回父代Pα和f(Pα)，输出当前最优解C、γ。

Step7：根据最优C、γ建立SVR预测模型。

其算法流程如图1所示。

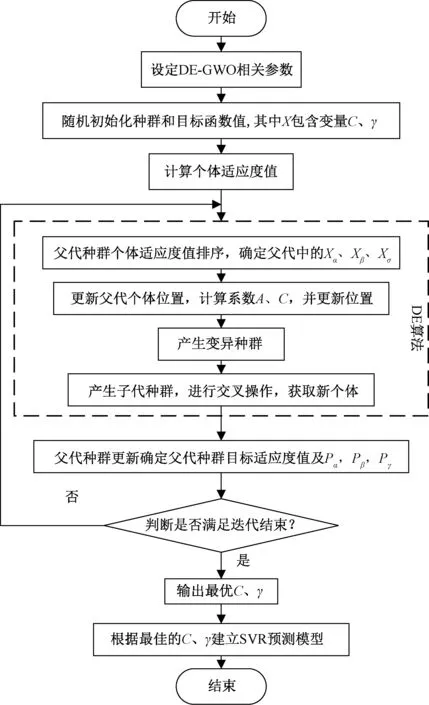
图1 DE-GWO-SVR算法预测流程

2 光伏输出功率的影响因素分析

影响光伏系统输出功率的因素较多，如光伏辐照强度、环境温度、风速、相对湿度等。实际工程中，光伏阵列输出功率表示为[20]：

Ppv=ηIsA[1-0.005(Tk+25)]

(16)

式中：η为光伏阵列的转化效率；Is为辐照强度，W/m2；A为阵列的总面积m2；Tk为大气温度,℃。

通常对某一特定的光伏电站，在进行短期功率预测时，其安装角度、阵列面积及光伏阵列转换效率为一常数，因此无需考虑。但日类型、辐照强度、温度、风速等对光伏输出功率均有一定的影响，因而本文通过对这些因素进行了研究。

2.1不同日类型的光伏输出功率

考虑到不同日类型下的光伏输出功率差异较大，因而应针对不同日类型分别进行预测。图2为晴天、多云和雨天3种常见日类型下美国俄勒冈州的某光伏电站在2015年7～8月的光伏功率输出。从图2中可以看出，晴天的光伏输出功率曲线最为平稳，且中午时分光伏输出功率达到最大值为12 000 W左右；而多云、雨天的光伏功率曲线随机性、波动性较大，这一情况不仅会影响光伏系统运行的可靠性，同时也会增加光伏预测的难度和预测误差。因此，针对不同日类型数据进行预测是十分必要的。

2.2气象要素对光伏输出功率的影响

如考虑将所有影响光伏功率的气象因子作为模型的输入变量，将会增加预测模型的复杂度及预测误差，因此本文选取光伏电站2015年4月～5月光伏辐照强度、环境温度和风速历史气象数据与光伏输出功率数据，利用Pearson秩相关系数法[21]进行分析，得到其秩相关系数结果如表1所示。

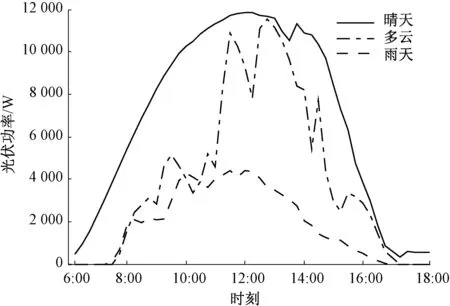
图2 不同日类型的光伏输出功率

由表1观察到，辐照强度与光伏功率呈现强相关性，而温度、风速与光伏功率呈现弱相关。考虑到这三者对光伏输出功率均会产生一定的影响，因此，本文将这三个气象因子的最大、最小和平均值作为DE-GWO-SVR模型的输入变量。

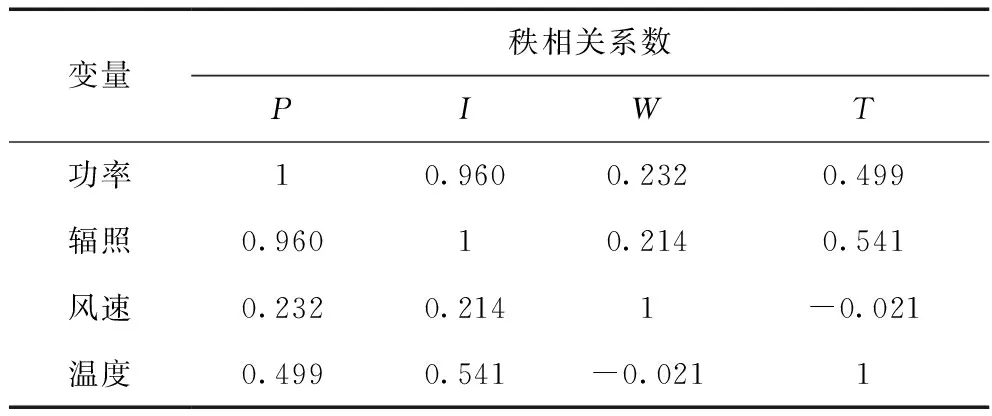
表1 Pearson相关系数分析结果 p.u.

2.3相似日理论

根据2.2节的分析，选取辐照强度、环境温度及风速作为影响光伏输出功率的气象因素。因此，可以设定每日特征向量为[22]：

(17)

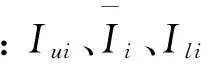
采用欧氏距离dij描述第i天与第j天之间的各气象总体差异度公式为：

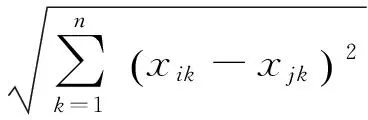
(18)

式中：n为特征向量的个数；k为特征向量的序号。根据式(18)求解与待预测日相似度高(即欧氏距离小)的多天作为预测日的样本集。

3 光伏功率预测建模

3.1数据处理

对光伏原始数据采用归一化预处理，其归一化的公式为：

(19)

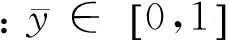
3.2建模流程

基于VMD-SE和DE-GWO-SVR的光伏功率预测模型，首先将光伏所有历史数据进行归一化预处理，再通过相似日计算选取与待预测日的相似样本。然后将所得相似样本中的光伏功率序列进行VMD分解并通过样本熵重组后形成随机分量、趋势分量和细节分量。其中，随机分量体现了光伏功率的随机波动性，因而SVR采用高斯径向基RBF核函数；趋势分量是光伏功率的主要构成分量，其曲线变化缓慢，可采用线性函数作为SVR的核函数；而细节分量体现了原始数据的细节波动情况，可根据试验选取RBF或Sigmoid函数作为核函数。最后，针对这三个分量分别建立DE-GWO-SVR预测模型，并将各分量预测结果求和相加得到最终的预测值。该算法的预测流程如图3所示。

4 仿真算例分析

4.1数据收集

以美国俄勒冈州的某光伏电站为研究对象，研究时段为2015年1月～2016年4月的06:00～18:00时间段，针对系统每5 min采集一次数据，本文选取1 h内每15 min的数据求平均值，总共49个点。将光伏数据经相似日理论分析后，根据不同日类型分别选取晴天数据样本85天，多云数据样本43天，雨天数据样本30天。对所有数据集采用归一化处理到[0,1]区间后，将75%的数据作为训练集，剩余25%的作为测试样本，建立提前1天的光伏输出功率预测。

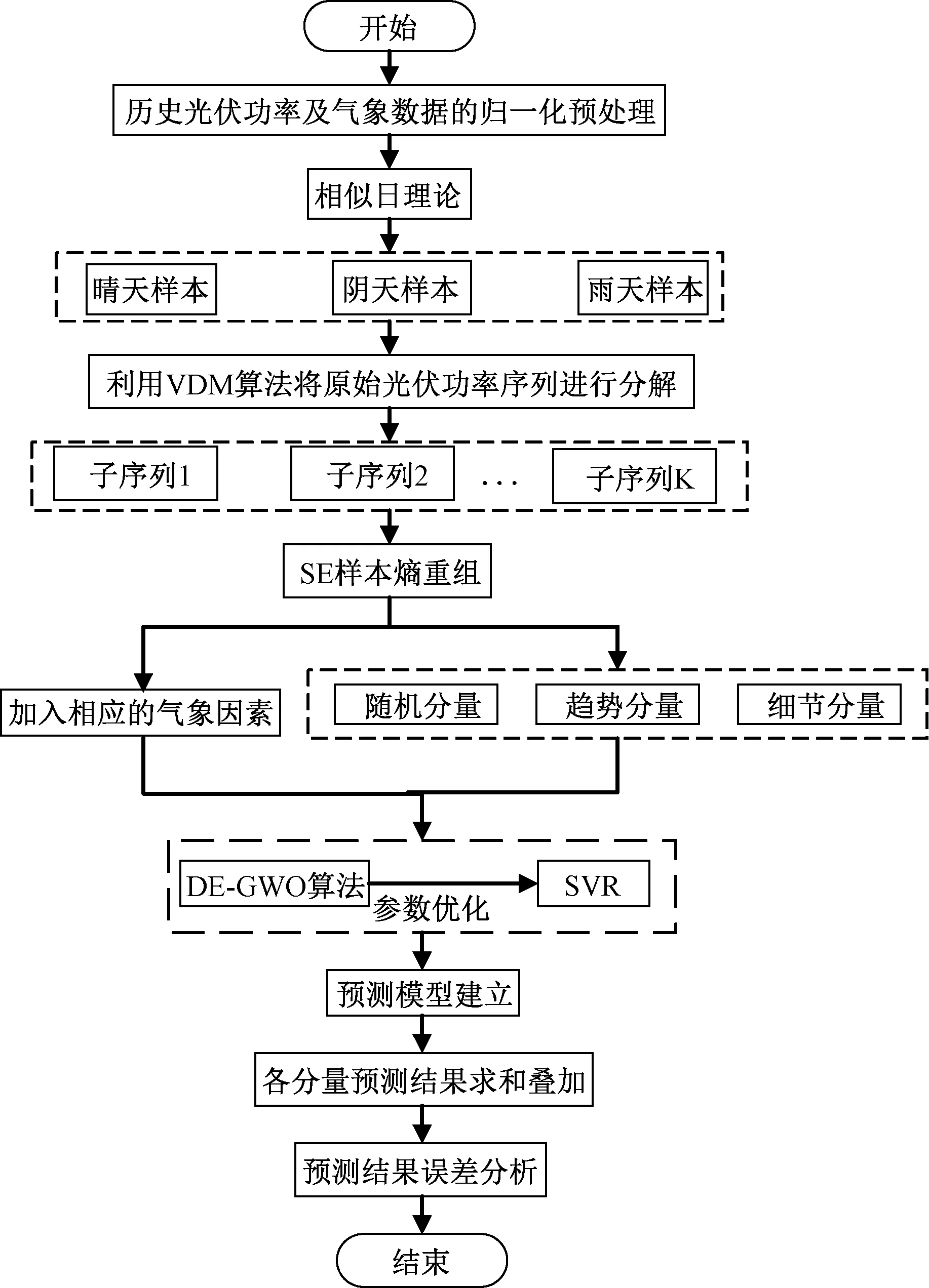
图3 基于VMD-SE-DE-SVR组合预测算法流程

4.2VMD-SE分析

以4.1节多云天气数据样本为例，将前32天作为训练集，后11天为测试集。对样本训练集和测试集的光伏输出功率序列进行VMD分解。考虑到VMD分解需提前设定模态数K，模态数过多会出现过分解，而过少会出现欠分解。因此，取模态数K范围为4～8，经过多次试验，当K>5时，出现中心频率相近的模态，因而，取K=5。图4为分解后的子序列。

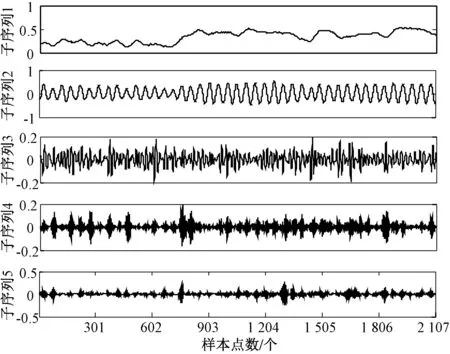
图4 多云天气光伏功率序列的VMD分解

若对分解后的每一子序列分别建立SVR预测模型将会增加计算规模。为减小计算规模，利用SE熵值对每一子序列的复杂度进行分析，再根据熵值将各子序列重新组合。图5为各序列熵值结果。

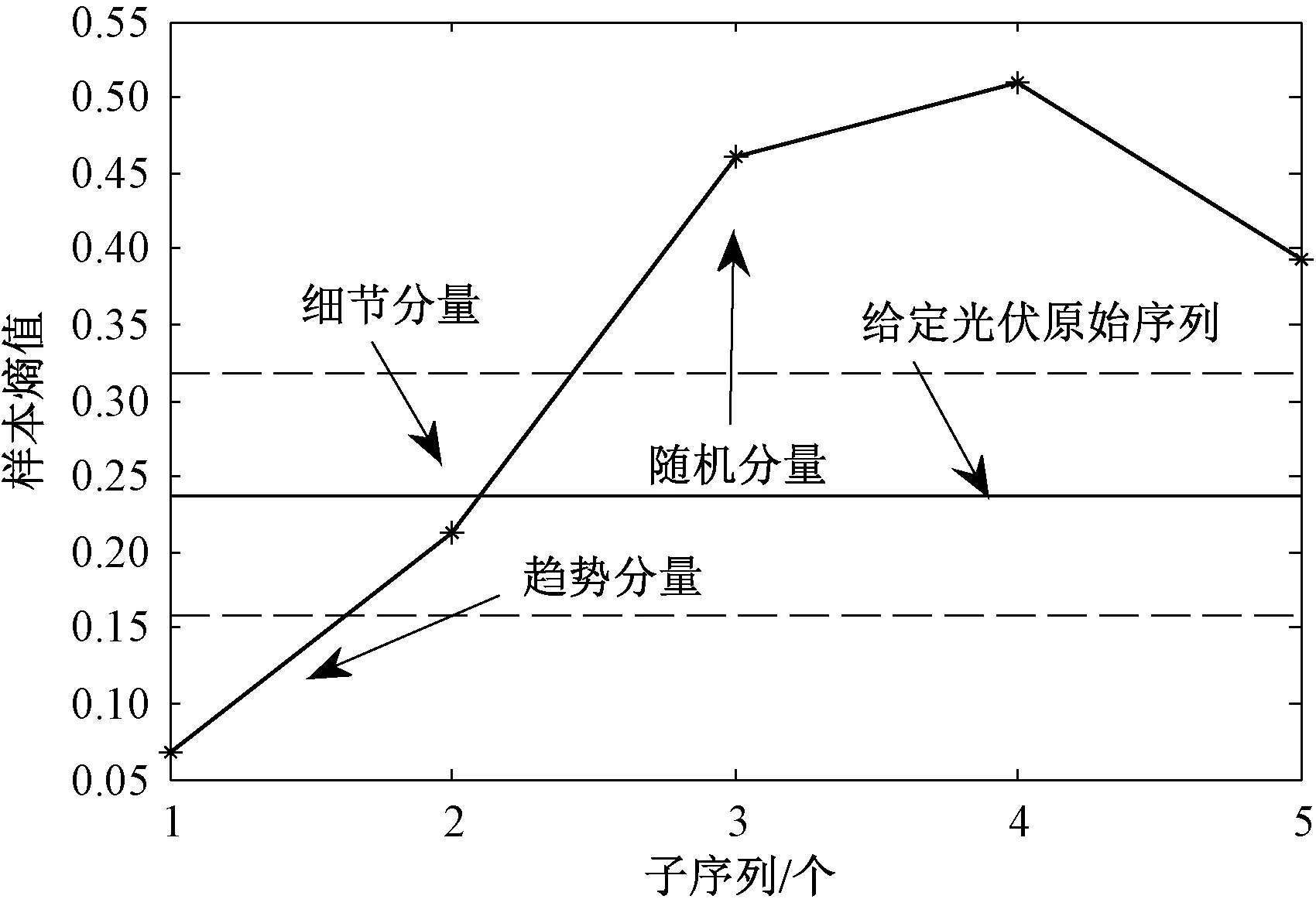
图5 各子序列的样本熵值

若取给定光伏序列样本熵阈值ψ变化范围为ψ=0.08，则根据样本熵重组规则，将子序列样本熵值大于给定光伏序列样本熵值范围内的序列构成随机分量；反之，子序列样本熵值小于给定光伏序列样本熵值范围内的序列构成趋势分量；而处于给定光伏序列样本熵值范围内的序列构成细节分量。因此，从图5可知，序列1为趋势分量，序列2为细节分量，序列3、4、5为随机分量。

4.3预测结果评价指标

采用归一化绝对平均误差eNMAE和归一化均方根误差eNRMSE作为误差评价指标，具体公式为：

(20)

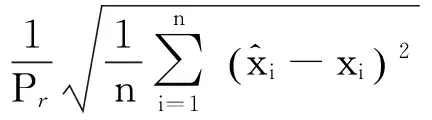
(21)

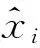
4.4仿真结果分析

为了验证本文所述预测模型的效果，按4.2节分析，根据得到的各分量与预处理后的气象数据形成预测样本集，针对晴天、多云日和雨天类型下的样本数据建立提前一天的SVR回归预测模型。同时，提出了以下几种模型进行比较分析：(1)基于VMD-SE和PSO-SVR、VMD-SE和DE-GWO-BP预测模型；(2)基于EMD-SE和DE-GWO-SVR预测模型；(3)基于VMD-SE-SVR预测模型。

为了公平起见，各预测模型的种群数目s均取20，最大迭代次数τmax为200，待优化变量维数为2。DE-GWO算法中，交叉概率Pc为0.25，缩放因子最大、最小值分别为0.8和0.2。PSO算法中，惯性权重系数为0.85，学习因子c1=c2=2。针对晴天、多云、雨天日类型下各方法预测结果如图6～8，预测误差指标结果见表2。

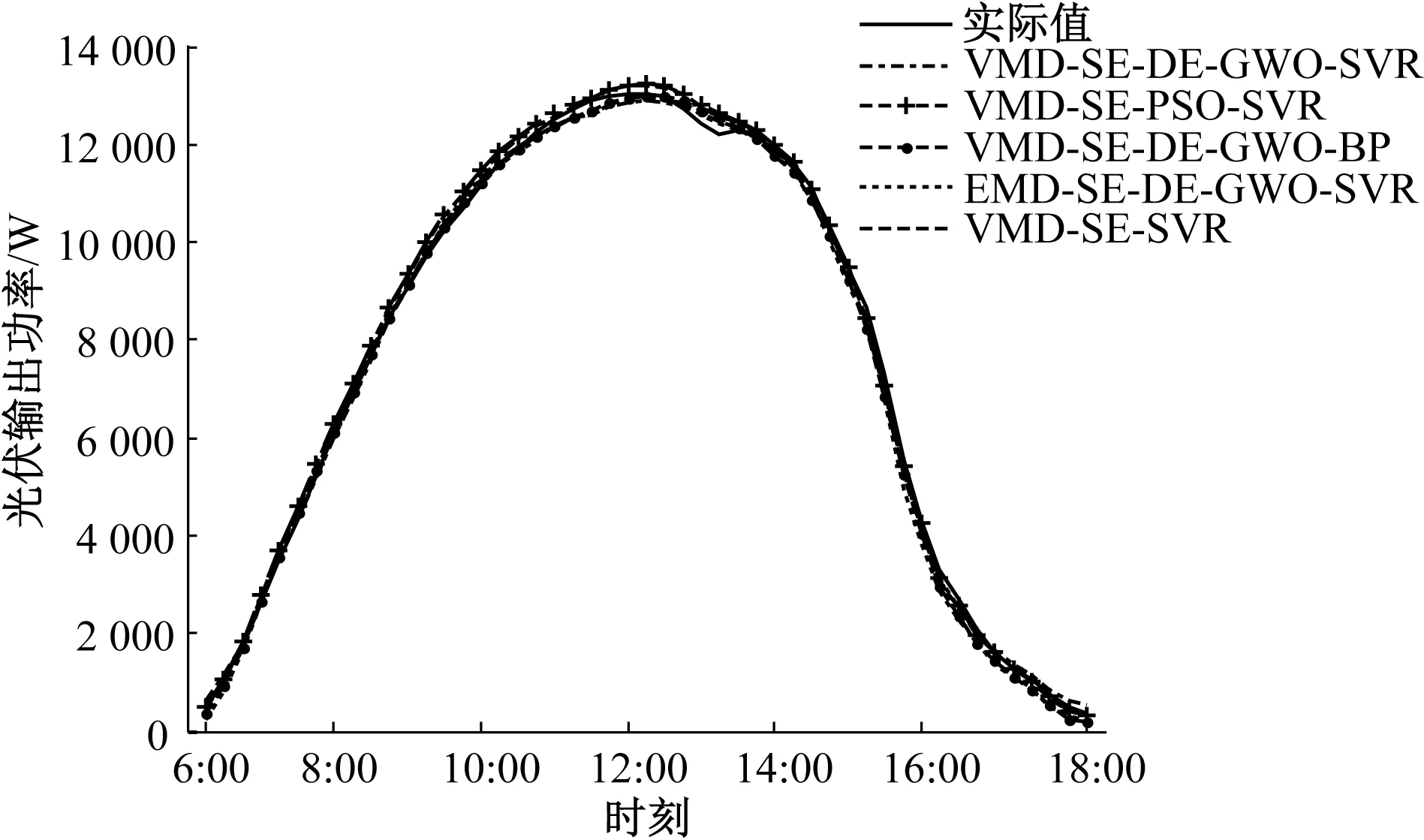
图6 不同算法下的晴天预测结果

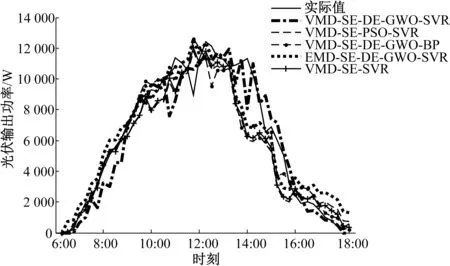
图7 不同算法下多云天气预测结果

图8 不同算法下雨天预测结果

从图6、7、8和表2可知：

(1)晴天时，各预测方法的预测精度均很高，eNMAE%和eNRMSE%均在5%以下；多云和雨天时，由于光伏输出功率具有较高的随机性和不确定性，因而其预测精度相比晴天预测精度有所降低，但总体上本文所提方法预测效果最佳。

(2)在VMD-SE分析前提下，DE-GWO优化SVR优于PSO优化SVR，说明DE-GWO优化算法能够更好地提高SVR的泛化能力和预测精度；而SVR模型与BP神经网络模型相比，不仅验证了SVR具有较强的泛化能力，而且也有效避免了BP固有的训练结果不稳定的缺陷。

(3)经VMD分解的预测模型相比EMD分解模型，其eNMAE%和eNRMSE%在阴天时均提高了2%左右，说明VMD分解能够有效克服EMD分解存在的模态混叠现象，降低预测误差。

(4)未经优化的VMD-SE-SVR预测模型的eNMAE%和eNRMSE%明显低于优化后的预测模型，说明SVR的参数优化是有必要。

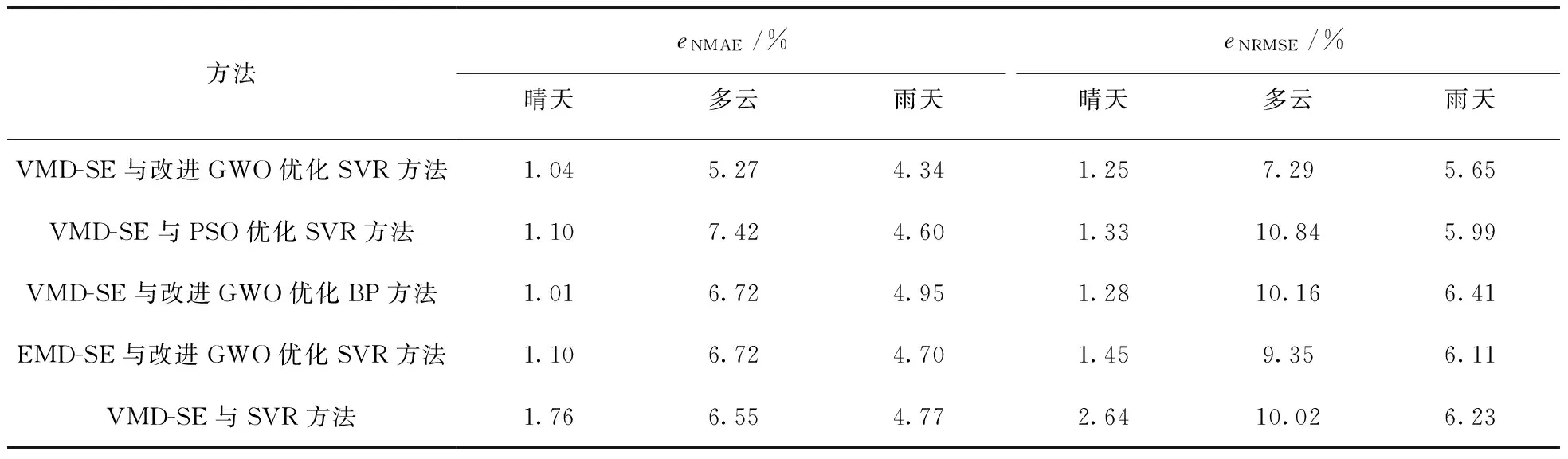
表2 不同算法的预测指标结果

5 结论

针对光伏输出功率的间歇性、随机性、波动性等特点，采用VMD分解技术对原始光伏功率序列进行分解，再将分解后的多个子序列进行样本熵重构以降低预测模型的复杂度，并根据SVR模型的小样本学习能力、学习速度快、泛化能力强的优点，充分运用SVR解决非线性问题的优势，考虑不同的环境影响因素作为模型的输入变量，对光伏功率进行回归预测。由于PSO算法在SVR参数寻优方面易陷入局部最优，导致算法收敛速度慢、预测精度较低，而本文提出的改进灰狼优化算法是通过模拟狼群的狩猎行为的新型智能算法，相对粒子群算法、BP神经网络算法等，更易跳出局部最优从而获得全局最优。通过实例结果表明，该算法在整体上大大提高了预测的准确性和预测效率，可以更好地保障电力系统的可靠运行。

[1] LI Y, HE Y, SU Y, et al. Forecasting the daily power output of a grid-connected photovoltaic system based on multivariate adaptive regression splines[J]. Applied Energy, 2016, 180(8):392-401.

[2]娄宝磊. 灰色动态BP神经网络在光伏短期出力预测中的应用[J]. 电气技术, 2015, 16(12):47-51.

[3]丁明, 王磊, 毕锐. 基于改进BP神经网络的光伏发电系统输出功率短期预测模型[J]. 电力系统保护与控制, 2012, 40(11):93-99.

[4]丁明, 徐宁舟. 基于马尔可夫链的光伏发电系统输出功率短期预测方法[J]. 电网技术, 2011，35(1):152-157.

[5]高阳, 张碧玲, 毛京丽,等. 基于机器学习的自适应光伏超短期出力预测模型[J]. 电网技术, 2015, 39(2):307-311.

[6]杨锡运, 刘欢, 张彬,等. 基于熵权法的光伏输出功率组合预测模型[J]. 太阳能学报, 2014, 35(5):744-749.

[7]张佳伟, 张自嘉. 基于PSO-BP神经网络的短期光伏系统发电预测[J]. 可再生能源, 2012, 30(8):28-32.

[8]徐敏姣, 徐青山, 袁晓冬. 基于改进EMD及Elman算法的短期光伏功率预测研究[J]. 现代电力, 2016, 33(3):8-13.

[9]张亚超, 刘开培, 秦亮. 基于VMD-SE和机器学习算法的短期风电功率多层级综合预测模型[J]. 电网技术, 2016, 40(5):1334-1340.

[10]DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3):531-544.

[11]WIDODO A, SHIM M C, CAESARENDRA W, et al. Intelligent prognostics for battery health monitoring based on sample entropy[J]. Expert Systems with Applications, 2011, 38(9):11763-11769.

[12]YANG H T, HUANG C M, HUANG Y C, et al. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output[J]. IEEE Transactions on Sustainable Energy, 2014, 5(3):917-926.

[13]吴米佳, 卢锦玲. 基于改进粒子群算法与支持向量机的变压器状态评估[J]. 电力科学与工程, 2011, 27(3):27-31.

[14]BAMAKAN S M H, WANG H, RAVASAN A Z. Parameters optimization for nonparallel support vector machine by particle swarm optimization [J]. Procedia Computer Science, 2016, 91(7):482-491.

[15]龙文, 赵东泉, 徐松金. 求解约束优化问题的改进灰狼优化算法[J]. 计算机应用, 2015, 35(9):2590-2595.

[16]徐松金, 龙文. 嵌入遗传算子的改进灰狼优化算法[J]. 兰州理工大学学报, 2016, 42(4):102-108.

[17]黄兴, 杨琳琳, 韩涛,等. 含风电机组的电力系统动态经济排放调度研究[J]. 电力科学与工程, 2014, 30(8):51-56.

[18]LUKE J, CHAKKARAVARTHY V, IRISAPPANE S, et al. Application of differential evolution algorithm in static and dynamic economic or emission dispatch problem: a review[J]. Renewable and Sustainable Energy Reviews, 2017，77(3)：1206-1220.

[19]ZHU A, XU C, LI Z, et al. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J]. Journal of Systems Engineering and Electronics, 2015, 26(2):317-328.

[20]王晓兰, 葛鹏江. 基于相似日和径向基函数神经网络的光伏阵列输出功率预测[J]. 电力自动化设备, 2013, 33(1):100-103.

[21]叶林, 陈政, 赵永宁,等. 基于遗传算法-模糊径向基神经网络的光伏发电功率预测模型[J]. 电力系统自动化, 2015，39(16):16-22.

[22]张华彬, 杨明玉. 基于天气类型聚类和LS-SVM的光伏出力预测[J]. 电力科学与工程, 2014, 30(10):42-47.

Photovoltaic Prediction Method Based on VMD-SE and Optimized Support Vector Machine

WU Xiaomei， ZHANG Qi， TIAN Mingzheng

(Faculty of Automation，Guangdong University of Technology，Guangzhou 510006，China)

Aiming at improving the short-term power prediction accuracy for photovoltaic station, a combination prediction method based on the VMD-SE and improved grey-wolf optimization algorithm to optimize the support vector regression is proposed in this paper. Due to the great difference of photovoltaic power output in different weathers, the data of the same weather are selected by selecting the similar days. Taking into account the strong random fluctuation of photovoltaic power output, the variational mode decomposition is used to decompose the original photovoltaic power sequence in order to reduce the non-stationary of the data. In order to overcome the disadvantage of blind selection of support vector regression parameters, the improved grey wolf optimization algorithm is applied to optimize the parameters to improve the prediction accuracy of the data. Finally, using sample entropy composed the subsequences and then summing them up, the final results are obtained. The results of a case shows that the combination forecasting method has the least overall prediction error, and it effectively improves the prediction accuracy for the PV output power, which can better guarantee the reliable operation of the power system.

photovoltaic power prediction; variational mode decomposition; differential evolution; grey wolf optimization; support vector regression; combination prediction

10.3969/j.ISSN.1672-0792.2017.09.005

TM615

A

1672-0792(2017)09-0029-08

2017-05-31。

中央财政支持地方高校发展专项资金项目(粤财教[2016]202号)。

武小梅(1972-)，女，博士，副教授，主要研究方向为新能源发电、电力市场；张琦(1992-)，女，硕士研究生，主要研究方向为新能源发电；田明正(1993-)，男，硕士研究生，主要研究方向为电力市场。