航运系统运价波动的周期性与平稳性研究

王佳莹，寇 莹，赵一飞

（上海交通大学 中美物流研究院,上海 200030）

航运系统运价波动的周期性与平稳性研究

王佳莹，寇 莹，赵一飞

（上海交通大学 中美物流研究院,上海 200030）

针对传统航运运价理论与实证分析结果的矛盾，对国际海运市场运价的周期性和平稳性进行了研究。首先利用传统ADF检验方法，发现海运运价整体样本（1976-2015）为平稳过程，而部分样本（1976-2002）为非平稳过程。其次，应用滚动平稳检验，发现运价的平稳性较为不稳定，并对样本起止时间点的变动较为敏感；将Zivot和Andrews模型改进后对航运周期内的运价进行平稳性检验，发现不同周期的运价平稳性差异较大，尤其2008年金融危机后，运价发生结构性改变并呈现较为稳定的平稳性运动。

航运系统；海运运价；平稳性；周期性；波动特征

1 引言

众所周知，国际航运市场与世界经济走势紧密相关。2008年全球金融危机后，航运市场受到巨大冲击而进入低迷状态，波罗的海干散货运价指数（Baltic Dry Index，BDI）断崖式下跌。航运市场是一个复杂的系统，其市场状态受到系统内外多种因素的影响，如全球经济走势、货运需求、船舶供给、战争、自然灾害等，使得海运运价波动具有不确定性特征。海运运价作为航运系统状态的直观体现，其波动特征受到货主、船东、船公司等各方的密切关注。

根据研究对象的不同，可将关于海运运价的研究分为两类，第一类集中分析单一运价序列，如Alizadeh和Nomikos[1]运用时间序列研究方法分析海运运价；Tvedt[2]从理论角度研究VLCC船型的运价短期形成机制；Kavussanos和Alizadeh[3]分析了海运运价的季节性特征；Veenstra[4]对运价进行了预测；余方平和匡海波[5]研究了BDI指数的波动幂律分布特性。第二类主要分析运价与其他航运市场变量的关系，变量包括新造船价格、载重吨位以及燃油价格等，如Beenstock[6]提出的运费市场与船舶市场相互关联的理论模型；Glen[7]研究了运价和吨位的相关性；Alizadeh和Talley[8]从微观角度研究干散货市场运价的影响因素；Xu等[9]和Kou和Liu[10]研究了干散货与油轮市场中船价与运价之间的领先-滞后关系；Tsolakis等[11]研究了二手船价与海运运价的关系；冯文文等[12]研究了新造船价格波动的形成原因和作用体系。上述文献大多数采用单位根检验对时间序列进行平稳性检验。相关结果表明，海运运价服从随机游走过程，但其一阶差分之后表现出平稳波动态势，即服从I(1)过程。基于这一结果，后续的相关研究通常采用协整检验和基于协整关系的因果检验。

传统航运理论中，运价通常被认为是由运输需求与供给共同决定[13,14]，尤其在散装船市场环境中（完全竞争市场）。运输需求高时，运价上升，随着运输收益的增加，供给增加，增加的供给又会拉低运价。反之，低需求造成运价下降，当市场消化多余供给后运价又会回升。因此，长期来看，运价由于供需关系的作用应围绕其长期均值上下波动，呈现平稳性波动。

显然，关于海运运价的平稳性，传统航运理论与实证检验结果之间存在矛盾，国内外学者针对这一矛盾进行的深入研究较少。根据平稳性理论，海运运价波动越剧烈，代表其偏离均值水平越远，越有可能造成非平稳的检验结果。本文对大量文献的研究样本区间进行梳理，发现过去的大部分研究均将目光聚焦于2002年之前的海运运价，其非平稳性的实证结论表明，2002年之前的海运运价可能存在“剧烈”波动。根据Stopford[13]提出的海运运价周期性理论，分隔航运周期的时间点前后，运价波动趋势变化明显，存在剧烈波动。

之前学术界主要采用定性的方法研究航运运价周期，如Stopford[13]结合航运市场发生的历史事件给出明确的周期分割点。定量划分运价周期的研究较少，仅Kou和Luo[15]从均值回归过程角度运用统计的方法找出周期分割点。但上述两方面分析都不涉及平稳性检验。本文需要从平稳性角度分割航运周期，因此基于结构突变的平稳性检验方法为本文提供了思路。在这一类方法中，选择Zivot和Andrews[16]模型（以下简称ZA模型）来寻找运价的结构突变时间点。ZA模型无法直接应用到本文中，原因在于：第一，该方法每次只能找到一个结构突变时间点，而海运运价存在多个周期，有多个结构突变点；第二，该方法能且一定能找到一个结构突变时间点，但对这一点前后是否确实发生“结构性”改变并没有做检验。因此，本文对ZA模型进行改进，使其成为适用于海运运价周期的方法。

综上所述，本文深入研究航运市场运价波动特征，从海运运价的周期性特点角度出发，首先探究运价是否如过去实证检验所示服从随机游走过程，还是如航运理论所说属于平稳运动过程；进而讨论造成理论与实证分析矛盾的因素，并研究其非平稳性结果是否由于周期性因素；最后将分析海运运价在2008年后是否表现出不同的特征与规律。

为深入研究以上内容，本文分三部分展开。第一部分，对海运运价在市场状态变化后，尤其是金融危机后回落到历史水平之后的平稳性进行再检验。针对过往研究集中在2002年前海运运价样本的局限，本文将海运运价的样本区间扩充至2015年底。第二部分，分析海运运价对于样本起止时间选取的敏感性，采用滚动平稳性检验进行实证分析，结果发现，海运运价的平稳性对样本起止时间点的变动较为敏感。第三部分，采用改进的ZA模型对样本进行周期确定，并检验海运运价的周期内平稳性。实证分析结果表明，第一，当下的海运运价呈现平稳性波动，符合航运理论；第二，周期性特征导致海运运价的平稳性受到样本起止时间影响较大；第三，不同航运周期的周期内运价平稳性差异较大，值得关注的是在2008年金融危机之后，航运市场显著改变，海运运价表现出显著平稳。

本文的研究完善了关于海运运价波动的理论与实证探讨，为其中存在的矛盾提出产生原因和依据。研究结果表明，海运运价波动的研究应考虑周期性因素，对不同周期内的海运运价的波动特征及联系进行深入研究或许更具有应用价值，本文应用修改后的ZA模型，精确划分出航运周期，为后续的相关研究提供了基础，有助于业内人士了解运价波动特征，有效规避风险。

2 研究方法

2.1 传统平稳性检验方法

本文采用Augmented Dickey-Fuller（ADF）检验方法对海运运价进行基本的平稳性检验。ADF检验包括无趋势平稳以及趋势平稳，其检验式见式（1）和式（2）。

其中yt代表被检验的序列；Δ表示一阶差分；u为常数项；t为趋势项；et为白噪声；k为滞后阶数。该检验的零假设（H0）为α=0，备择假设（H1）为a＜0。拒绝H0代表时间数列yt非平稳，即存在单位根。式（1）表示yt围绕水平均值u波动，无趋势，而式（2）表示yt围绕趋势线u+bt波动。

首先选用包含趋势项的式（2）来估计各个参数，再检查趋势项的显著性，如不显著表明趋势不明显，则采用式（1）重新估计参数，得出平稳性分析结果。滞后阶数k选用施瓦茨信息准则（Schwarz Information Criterion，SIC）选取。

2.2 样本起止时间对平稳性结果的影响-滚动平稳检验

为检验样本起止时间点的选择对平稳性的影响，本文参考Banerjee等[17]的滚动检验方法。对于时间序列{y1,y2,…,yT}，首先，限定初始子样本长度为j，即初始样本为{y1,y2,…,yj}。随后，每次将样本起止时间点同时向后移动一位，直到子样本的终点为整体样本的终点为止，即{y2,y3,…,yj+1}…{yT-j+1,yT-j+2,…,yT}。再针对这一系列的子样本进行传统ADF检验，如图1所示。由于不同周期内的运价可能呈现上升、下降或水平几种可能趋势，因此，此处将选用式（2）对周期内样本做ADF检验。

图1 滚动平稳检验样本选取方法

2.3 海运运价周期区分方法

检验周期性是否影响海运运价的平稳性，需要首先对运价的波动周期进行划分，即寻找各个周期间的分割点。本文以ZA模型为基础，对其方法进行改进，使其适用于本文的研究。首先，ZA模型在式（2）的基础上考虑一个内生的结构突变点，该突变点存在三种类型—截距突变（模型A）、斜率突变（模型B）以及截距斜率均突变（模型C）。由于不同航运周期内，海运运价的改变既可能发生截距上也可能发生趋势上，因此本文选取包含这两种情况的模型C做后续检验。对于yt序列，模型C公式如下：

为适应海运运价周期特征，本文对模型C的应用进行改进，包括以下四点：

（1）在结构突变点Tλ的选择上，ZA模型根据â的t统计量（以下简称t(â)），通过选择最小值tmin(â)，对应的时间点得到Tλ。由于tmin(â)一定存在，也就意味着对于任意给定样本，Tλ一定存在。然而Tλ前后运价是否发生了显著性改变不能通过t(â)判断，而是需要进一步检验虚拟变量DUt与DTt的显著性。若其中任意一个变量显著（本文设定5%的显著性水平），则表明运价发生“结构性”改变，此时tmin(â)所对应的时间点才能认为是Tλ。若两变量均不显著，则表示结构性改变不明显，tmin(â)所对应的时间点不是Tλ。

（2）λ的通常取值范围为[0.15,0.85]。Stopford[13]指出，干散货船在1947-2007年间，航运周期较短，高峰期平均2.4年，低谷期平均3.2年。本文假定海运运价周期的最小长度为2年，并根据子样本的长度T设定λ值，即对于月度数据来说，λ的范围为，以保证周期分割点前后的样本量最少有24个月。

（3）λ的限定范围使得子样本量T需满足T＞48个月。由于要检验运价周期内的平稳性，要求一个周期的样本长度要满足单位根检验的要求。样本量很小时，得不到有意义的结果。因此本文适当放宽子样本的数据量，参照Stopford[13]给出的平均航运周期，设定Tmin=6年=72个月。

（4）应用上述方法仅能在样本中找到一个或零个Tλ，而运价的波动过程包含多个航运周期，存在多个Tλ。本文参考Kou和Luo[15]提出的divide-and-conquer策略进行多点寻找。

综上，运价周期区分的算法流程如图2所示。首先判断初始样本大小是否大于71个观测值，满足则采用模型C估计系数，根据tmin(â)找到对应的时间点，再根据时间点对应的虚拟变量DUt和DTt的显著性，判断这一时间点是否为周期分割点。如果至少有一个变量显著，则分割点确定，否则停止寻找。对于产生的每个子样本，运用相同的方法寻找Tλ。算法包含两个终止条件，虚拟变量的显著性以及子样本包含的观察期数量限制。

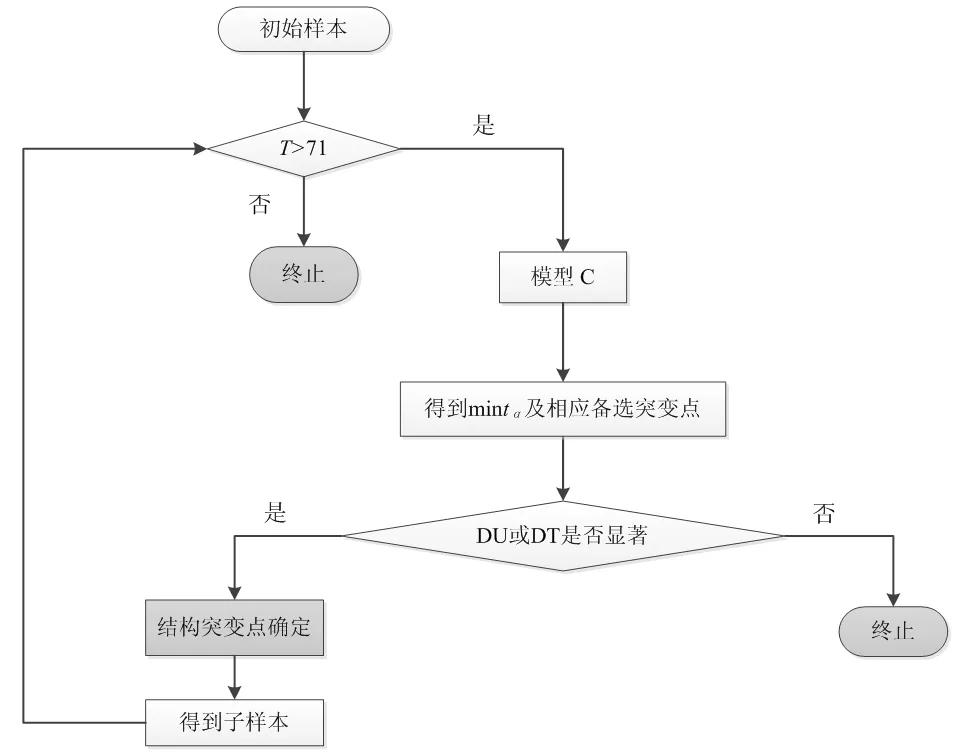
图2 基于结构突变理论的周期确定算法流程

3 实证分析

本部分对海运运价的平稳性进行实证分析。选取巴拿马型干散货船的运价作为分析对象，其中包括：运价指数(Baltic Panamax Index，BPI)，航次租金费率(Time Charter Equivalent，TCE)，1年期租船费率(1-year Time charter，TC1)的月度数据，数据均来自Clarkson Shipping Intelligence Network。以上三个变量所对应的样本起点分别为1998年5月、1993年1月、1976年1月，样本截止时间均为2015年12月。

3.1 传统平稳性检验

应用2.1节提到的方法对初始整体样本进行平稳性分析，检验结果见表1。结果表明，四种形式的海运运价与航运理论一致，都不含趋势项，即海运运价长期围绕水平均值波动。与过去实证分析结果不同的是，检验结果表明三种形式的海运运价均拒绝ADF零假设，表明海运运价不包含单位根（10%显著性水平），即符合航运理论所述的平稳性运动过程。

为对比与过去海运运价的实证研究，将子样本截止时间设定为2002年12月，ADF检验结果见表1右部分所示。可见，子样本所选用的ADF检验模型仍不含趋势项，但平稳性结果与过去实证分析结果大体一致，除TC1外，其他两种形式运价均包含单位根。由此可见，随着时间推移，海运运价的平稳性产生了变化。

表1 巴拿马船型海运运价整体与部分样本的ADF检验

3.2 滚动平稳性检验

应用2.2节提出的滚动检验方法，检验样本起止时间点的变化对运价平稳性的影响。本节选取数据较为完整的TC1作为代表进行后续分析。j设定为一个平均周期的长度（7年），滚动检验结果如图3所示。图中实线代表式（2）中t(â)，虚线代表t(â)对应的p(â)，横轴对应每个子样本的终点。可见，p(â)的波动较为剧烈，虽大部分时间位于5%的水平线之上，部分时间段里也会位于5%水平线下方。这一结果表明，TC1的平稳性受样本起止点影响较大，且在某些时间段呈现平稳波动的实证分析结果。

图3 滚动ADF检验t(â)和p(â)值

3.3 运价周期分割点的确定

运用2.3节的运价周期区分方法，最终确定11个周期分隔点，即TC1在1976年1月至2015年12月期间，有12个航运周期。表2为TC1周期分割点寻找步骤以及检验结果。

表2 运价周期分割点的确认步骤及结果

将表2结果标注到原始TC1序列中，如图4所示，首个分割点为1981年4月，对应由美国煤炭工人罢工运动引起的世界经济严重衰退，此前海运运价呈上升趋势，而之后迅速下降，直到第二个分割点1985年5月为止。第三个分割点为1987年8月，在这点前，运价波动较小，而后运价水平有较明显的提高。第四个分割点为1994年10月，这点之后直到第五个分割点前（1994年10月），运价波动较贴近航运理论围绕水平均值上下波动。第六个分割点为1997年11月，这一时间点对应于亚洲金融危机的全球性影响。第七个分割点为2001年4月，这一点后到下一分割点2003年11月前，中国经济快速增长，带动航运市场的繁荣和运价的上升。第九个分割点为2006年7月，航运市场进入到历史上最繁荣的时期，大量资本涌入，导致运价直线上涨，运价的疯狂上涨引发造船买船热潮，由于二手船能够较快进入航运市场，此段时期的二手船价格甚至高于新船价格。这样的市场情景维持到第十个分割点—2008年9月，也就是众所周知的美国次贷危机引发的世界性经济衰退，海运运价急速下跌，在这之后虽有一段小幅上涨，但由于之前造船过多，市场上船舶供给量过大，而中国经济放缓，运价再度下跌，2010年10月后，已逐渐恢复到历史水平。

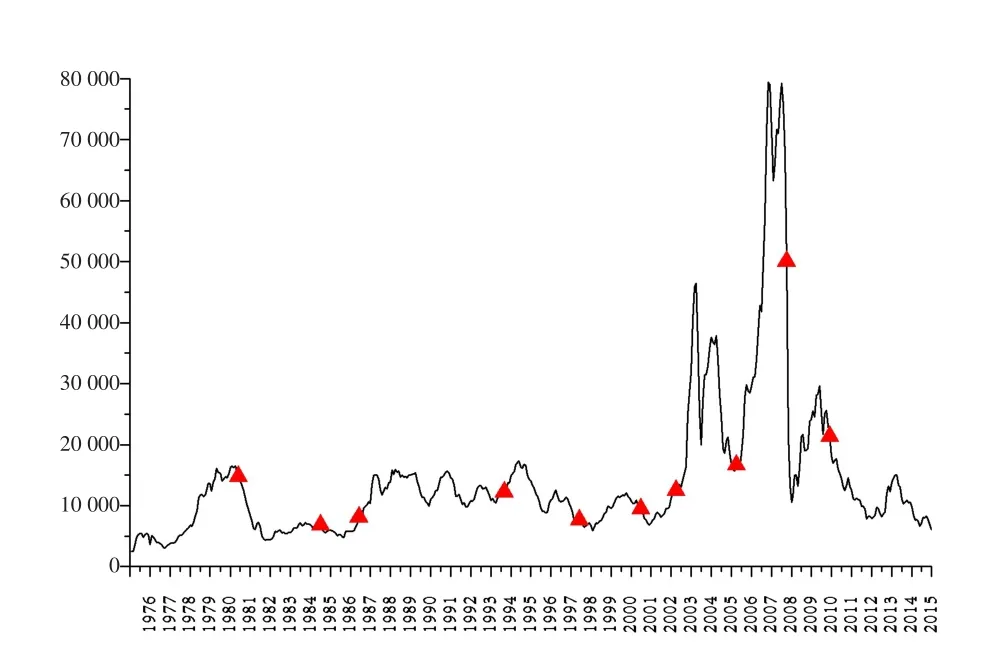
图4 巴拿马船型1年期租船运价周期

3.4 运价的周期平稳性检验

由于运价在周期内部表现出某一特定波动趋势，针对3.3节得到的12个航运周期进行周期内ADF检验，检验结果见表3。从表中结果可以看出，第2、4、5、9、11五个周期内的运价都表现为平稳（或趋势平稳），最后一个周期运价也趋向平稳。其中，第1、4、12周期相对较长，而其他周期较短，平稳性结果的不一致说明样本长度并非影响平稳性检验结果的关键因素，而运价周期起止点的选择对平稳性结果影响较大。

表3 航运周期内ADF检验结果

由于较短的周期内样本观测值较少，平稳性分析的结果可能由于数据量的限制而存在偏差。因此本文将两个相邻的航运周期合并为一段待检测样本，检验其平稳性。首先基于已有分割点，生成每段子样本的DUt与DTt序列，然后应用式（3）计算 â，判断零假设α=0是否被拒绝。值得注意的是，分割点此时为已知，t(â)临界值不同于ZA模型，因此将参考Perron[18]的外生结构突变点的临界值。

检验结果见表4。大多数结果显示，模型C的t(â)比ADF的t(â)有所增加，表明考虑结构突变时运价会更接近平稳性结果，尤其样本周期8&9显示出两种方法的显著差异，当应用ADF检验时，运价序列不平稳，而应用模型C时，序列平稳。不难看出，原本平稳的序列改变起止时间之后可能变为非平稳状态，如样本周期1&2和2&3。而当时间序列样本长度增加，序列也不一定变的平稳，例如样本周期6&7和7&8。

表4 相邻航运周期内运价的平稳性检验结果

由此可见，样本所选取的起止时间点对海运运价的平稳性影响较大，运价的周期平稳性特点较为明显。往后研究者分析海运运价的平稳性时，建议将其周期性特点加以考虑，尤其进行运价预测时，采用大量的历史数据进行全样本分析未必会得到理想结果，应用周期内数据分析运价运动过程也许更为准确。此外，所有实证分析结果都显示，在2008年美国次贷危机之后，海运运价的波动表现出非常显著的平稳性特点，2008年后，海运运价发生结构性改变，其周期特征与规律需要重新认识。

4 结语

本文从目前海运运价回落到历史水平的现实角度出发，重新审视与分析了海运运价的平稳性，并对过去检验结果与传统理论相矛盾的原因进行深入探讨。对更新后的样本进行传统单位根检验的结果显示，海运运价的运动过程与过去的实证分析结果矛盾，变为平稳运动过程。应用滚动平稳检验方法，对运价的平稳性检验结果做敏感性分析，发现运价的平稳性对样本起止时间点的变化较为敏感。为检验海运运价周期性对平稳性的影响，本文改进ZA模型，对巴拿马期租船费率进行周期划分，精确找出11个周期分割点，结合航运历史事件，本文结果与历史上相关事件基本吻合。随后应用传统ADF以及考虑结构突变点的平稳性检验对运价进行了周期内平稳性检验。结果证实，运价周期是影响单位根检验结果的重要因素，运价普遍存在周期内平稳的特点。此外，本文发现2008年后运价波动呈现与以往不同的运动特征，表现出非常显著的平稳性，意味着干散货运价发生结构性变化，应对其重新认识与研究。

本文从海运运价周期性特性及周期内平稳性角度入手，将航运市场的周期特性与运价影响有机结合起来，为研究国际航运市场周期性变化以及未来发展趋势提供了一个全新的视角。海运运价的波动过程复杂多变，在各个周期可能呈现出极为不同的运动趋势，单一的从整体角度总结其服从平稳性或非平稳性运动过程并不精确，尤其在以预测为目标时，选择过多的历史数据未必得到更准确的结果，选择周期内数据也许能够更好地把握市场走向。本文研究结论完善了航运市场周期波动理论，无论对于微观的船公司层面或是宏观的政策层面，均为其进一步掌握航运市场周期以及波动特性提供了新的量化参考标准以及实证检验方法，值得航运界参考。

[1]Alizadeh H A,Nomikos K N.Dynamics of the term structure and volatility of shipping freight rates[J].Journal of Transport Economics and Policy,2011,45(1):105-128.

[2]Tvedt J.Short-run freight rate formation in the VLCC market:A theoretical framework[J].Maritime Economics&Logistics,2011,13(4):442-455. [3]Kavussanos M G,Alizadeh-M A H.Seasonality patterns in dry bulk shipping spot and time charter freight rates[J].Transportation Research Part E:Logistics and Transportation Review,2001,37(6):443-467.

[4]Veenstra A W,FransesP H.A co-integration approach to forecasting freight rates in the dry bulk shipping ector[J].Transportation Research Part A,1997,31(6):447-458.

[5]余方平,匡海波.基于跳跃时间和幅度的BDI指数波动幂律分布特性研究[J].系统工程理论与实践,2017,37(3):607-619.

[6]Beenstock M.A theory of ship prices[J].Maritime Policy and Management,1985,12(3):215-225.

[7]Glen D R.The market for secondhand ships:further results on efficiency using cointegration analysis[J].Maritime Policy&Management,1997,24(3):245-260.

[8]Alizadeh H A,Talley K W.Microeconomic determinants of dry bulk shipping frieght rates and contract times[J].Transportation,2011,38(3):561-579.

[9]Xu J J,Yip T L,Liu L.A directional relationship between freight and newbuilding markets:A panel analysis[J].Maritime Economics&Logistics,2011,13(1):44-60.

[10]Kou Y,Liu L.Comparison between dry bulk and tanker shipping:empirical evidence from temporal relations between freight rate and ship prices[A].The 4th International Conference of Asian Shipping and Logistics[C].2011.

[11]TsolakisS D,Cridland C,Haralambides H E.Econometric Modelling of Second-hand Ship Prices[J].Maritime Economics&Logistics,2003,5(4):347-377.

[12]冯文文,匡海波,武华华,等.基于耦合的新船价格波动影响因素分析[J].系统工程理论与实践,2016,36(11):2 879-2 888.

[13]Stopford M.Maritime economics(3rd edition)[M].USA:Routledge,2009.

[14]Varnavides L,Karakitsos E.Maritime economics:amacroeconomic approach[M].UK:Palgrave Macmillan,2014.

[15]Kou Y,Luo M.Modelling the relationship between ship price and freight rate along with structural changes[J].Journal of Transport Economics and Policy,2015,49(2):276-294.

[16]Zivot E,Andrews K.Further evidence on the great crash,the oil price shock,and the unit root hypothesis[J].Journal of Business and Economic Statistics,1992,10(3):251-270.

[17]Banerjee A,Lumsdaine R L,Stock J H.Recursive and sequential tests of the unit root and trend-break hypotheses:theory and international evidence[J].Journal of Business and Economics Statistics,1992,10(3):271-287.

[18]Perron P.The great crash,the oil price shock,and the unit root hypothesis[J].Econometrica,1989,57(6):1 361-1 401.

Study on Cyclicity and Stability of Transport Price Fluctuation in Shipping System

Wang Jiaying,Kou Ying,Zhao Yifei
(Sino-US Logistics Research Institute,Shanghai Jiaotong University,Shanghai 200030,China)

In this paper,in view of the contradiction between the transport price theory and the findings from empirical industrial studies,we studied the cyclicity and stability of the transport price in the international shipping market.First,using the traditional ADF process,we found the overall sample for the period between the year 1976 and 2015 exhibited stability while the partial sample for the period between 1976 and 2002 showed instability.Then,through rolling stability test,we found the transport price was unstable and rather sensitive toward the change in the starting and ending year of the sample.Further,after improving the Zivot and Andrews model,we had a stability check of the transport price within the shipping cycle which revealed great difference between the price stability in different cycles,particularly after the 2008 financial crisis when the transport price underwent structural change and took on a more stable trend.

shipping system;marine shipping price;stability;cyclicity;fluctuation characteristics

F550.5

A

1005-152X(2017)09-0062-06

10.3969/j.issn.1005-152X.2017.09.014

2017-08-01

国家自然科学基金青年科学基金（71608164）

王佳莹（1992-），女，浙江舟山人，硕士研究生，研究方向：航运运价波动；寇莹（1982-），通讯作者，女，辽宁沈阳人，助理研究员，研究方向：航运运价波动、航运业碳减排、船舶投资；赵一飞（1962-），男，上海人，副教授，研究方向：航运与物流管理、多式联运。