基于六自由度动力学模型的火箭推力下降故障仿真

王志祥，李家文，李道奎

基于六自由度动力学模型的火箭推力下降故障仿真

王志祥，李家文，李道奎

（国防科学技术大学航天科学与工程学院，长沙410073）

发动机推力下降会导致运载火箭质心偏移、产生推力不平衡力矩、减弱控制力等后果，导致火箭姿态和飞行轨迹发生改变，影响火箭可靠性和发射成败。针对某型捆绑火箭助推段发动机推力下降故障问题，建立了故障下的火箭刚体六自由度动力学模型，基于Matlab／Simulink软件，采用分层模块化建模思想搭建了全数字仿真模型，最后以发动机正常状态和单台发动机推力下降为例给出了仿真算例。结果表明，该仿真模型能够正确地反映推力下降故障下捆绑火箭助推段的飞行特点。

运载火箭；六自由度模型；推力下降；故障仿真

Abstract： The thrust decline of the launch vehicle leads to the deviation of the mass center， the imbalance thrust torque and the weaker controlling force，thus results in the change of the flight altitude and the flight path.Even worse， the launch of the rocket may fail.As a result， the thrust decline of engine was studied in this paper.Based on the loss of thrust，a modularized simulation method was developed for launch vehicle by applying the Matlab／Simulink.Then the influences of the failure of booster engine and core engine were investigated by failure simulation.The simulation results demonstrated that the proposed model could correctly reflect the flying characteristics of the launch vehicle with thrust decline.

Key words：launch vehicle； six DOF model； thrust decline； failure simulation

1 引言

液体火箭发动机由于结构复杂、工作环境恶劣，发生故障的概率很高，最常见的故障就是推力下降甚至关机［1］。发动机推力下降会导致三个方面的严重后果：一是导致相应储箱推进剂消耗缓慢，致使箭体质量分布不对称，引起箭体质心偏移；二是产生推力不平衡干扰力矩，加大姿态控制难度；三是降低摆动发动机的控制力矩。由于发动机推力下降甚至关机导致的事故非常多，据统计，1984年长征三号发射试验通信卫星，由于液氧发动机不能再次点火，卫星未能进入预定轨道；1991年长征三号发射通信卫星，由于火箭发动机提前关机，卫星未能进入预定轨道［2］。2012年美国Space X公司的猎鹰9号运载火箭升空80 s后，1号发动机推力异常而被姿控系统提前关闭［3］。因此，开展发动机推力下降故障下运载火箭动力学建模和故障影响仿真分析，对运载火箭可靠性、安全性和发射成功率的提高都具有重要意义。

发动机故障不仅可能影响姿态，而且可能导致飞行轨迹偏离程序弹道，因此，完整的故障仿真应基于六自由度运动模型开展。近年来，许多学者对火箭六自由度动力学仿真开展了研究，但对推力下降故障下的运载火箭六自由度故障仿真研究较少。李新国等［4］基于Open Flight仿真平台搭建亚轨道飞行器三自由度飞行故障仿真系统并进行了故障仿真研究，分析了推力损失对亚轨道飞行器上升段飞行轨迹的影响。程龙等［5］基于Matlab／Simulink软件对发动机故障下火箭飞行进行了故障仿真。傅维贤等［6］对导弹的典型故障进行了仿真分析，并给出了一系列硬件故障的研究结果。以上均未对发动机推力下降对运载火箭动力学模型及飞行参数的影响进行详细的介绍。

本文将以某捆绑火箭为对象，基于Matlab／Simulink的仿真平台，针对助推飞行段发动机推力下降故障对捆绑火箭姿态和飞行轨迹的影响开展仿真研究。首先给出考虑发动机推力下降故障的火箭六自由度刚体动力学模型，然后搭建相应的全数字仿真模型，最后基于该模型进行发动机推力下降故障仿真，以验证模型有效性。

2 考虑推力下降故障的火箭刚体运动模型

以某型号火箭为研究对象，在火箭的助推飞行段，芯级有两台发动机，按“＼”型布局，作“+”字摆动；助推有四台发动机，按“+”型布局，作切向摆动，各发动机摆角按如图1所示方向为正。

图1 一级发动机布局及摆动示意图Fig.1 The layout and swing of the first stage engine

芯级发动机额定推力大小为Pxj，助推发动机额定推力大小为Pzt，芯级发动机和助推发动机推力作用点到芯级纵轴的距离分别为r0、r1。芯级和助推发动机摆角分别为δxji、δzti，i＝1，2，3，4，由于发动机摆角较小，因此可以认为sinδ≈δ，cosδ≈1。

本文主要考虑推力下降故障模式为发动机推力输出为恒值，即发动机推力迅速下降到某一固定值，输出为小于额定值的某一恒值，该型故障特征量主要有故障发生时间和发生故障后发动机输出推力大小。以芯级1号发动机为例，发动机推力迅速下降到某一固定值时推力曲线图如图2所示。

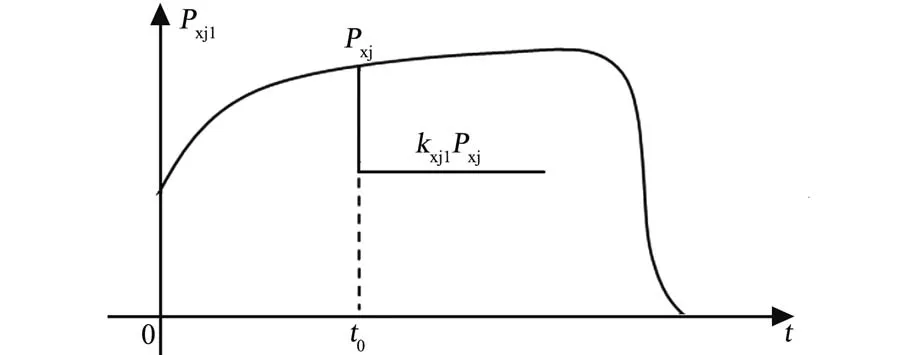
图2 推力曲线示意图Fig.2 Diagram of thrust curve

相应的数学模型如式（1）：

其中，kxj1、kxj2、kzt1、kzt2、kzt3、kzt4分别为各个发动机发生推力下降故障后发动机输出推力大小与额定推力的比例系数；Pxj1、Pxj2、Pzt1、Pzt2、Pzt3、Pzt4分别为各个发动机发生推力下降故障后输出的推力值。

2.1 考虑推力下降故障的火箭六自由度刚体动力学模型

相比于火箭正常飞行时的动力学模型，推力下降时火箭的动力学模型需考虑引言所述三种故障后果的情况。考虑到火箭助推飞行段时间较短，忽略地球自转的影响。 参考文献［7～9］，可建立考虑发动机推力下降故障的火箭六自由度刚体动力学模型如式（2）、（3）：

其中：m为箭体质量，V为箭体相对地球的速度，θ为速度倾角，σ为航迹偏航角；、分别为发射坐标系、速度坐标系和箭体坐标系到半速度坐标系的方向余弦阵；Fcm为箭体质心偏移产生的偏心干扰力；P为发动机推力；Fc为控制力；FI为发动机摆动惯性力；FB为风干扰及结构干扰力；G为重力；R为气动力；Mcm为箭体质心偏移产生的偏心干扰力矩；MP为推力不平衡力矩；Mc为发动机控制力矩；MR为气动力矩；MI为发动机摆动惯性力矩；MB为风干扰力矩和结构干扰力矩；ω为箭体相对地球转动角速度在箭体几何坐标系中的矢量；J为箭体相对箭体几何系的惯量张量，当发动机未发生推力下降故障时，箭体质量分布对称，所以Jx1y1＝Jx1z1＝Jy1z1＝0，当发动机发生推力下降故障时，由于质量分布不对称，则 Jx1y1、Jx1z1、Jy1z1均不为零，推力下降故障下惯量张量J表达式为式（4）：

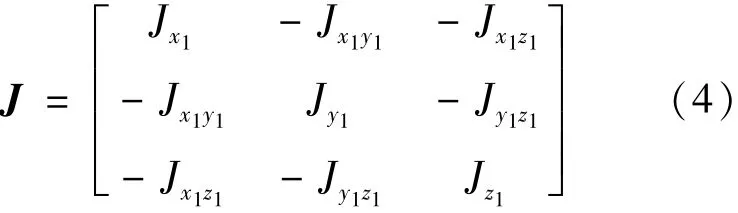
1）偏心干扰力Fcm和干扰力矩Mcm

如前所述，发动机推力下降将导致相应储箱推进剂消耗缓慢，致使箭体质量分布不对称，引起箭体质心偏离箭体纵轴。质心偏移产生的干扰力在箭体系中的分量为式（5）：

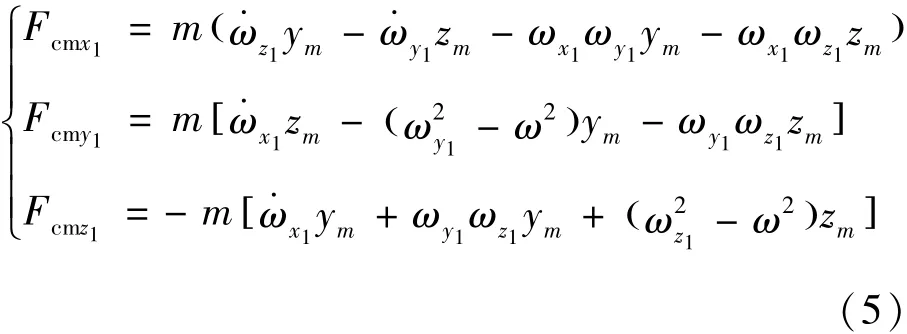
干扰力对箭体坐标系原点的力矩为式（6）：

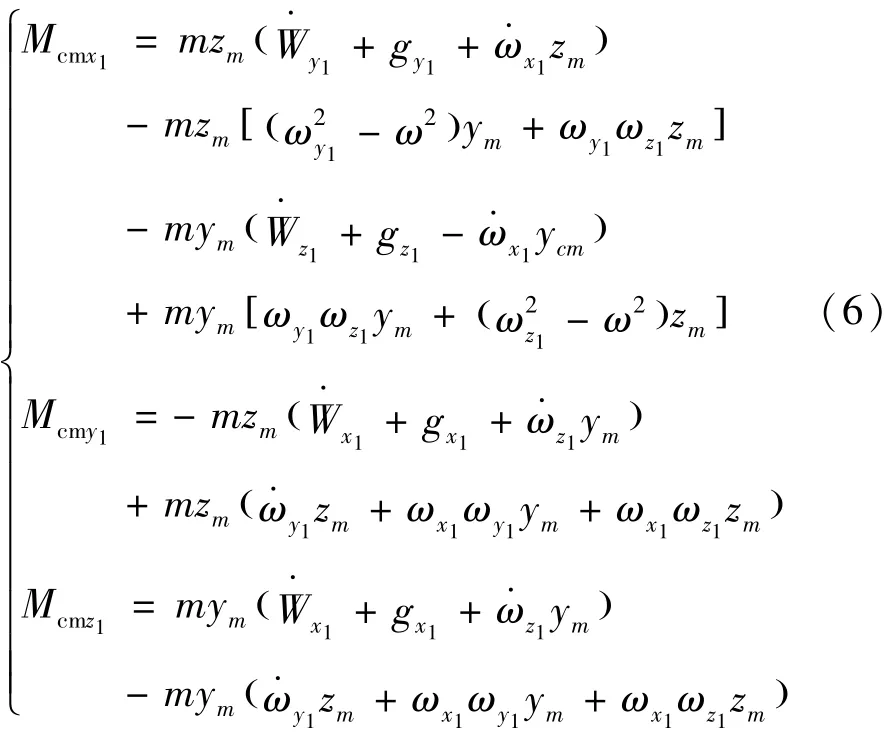
其中： ωx1、ωy1、ωz1为箭体相对地球转动角速度在箭体几何系中的分量，ω为箭体转动角体视加速度和重力加速度在箭体系中的分量；ym、zm为箭体瞬时质心在箭体几何坐标系中的坐标。

2）发动机推力P及力矩MP

如果发动机摆角为小角度，推力在箭体系中的分量为式（7）：

正常情况下，捆绑火箭发动机均为轴对称布置，各发动机推力对箭体质心的合力矩为零，不应产生不平衡力矩。但某个发动机推力下降后，与其对称布置的另一台发动机由于推力较大，就会产生不平衡力矩。例如当助推1号发动机推力下降时，助推1、3号发动机推力不再相等，助推3号发动机在俯仰轴方向产生的控制力矩无法由助推1号发动机来抵消，因此会出现一个附加的干扰力矩。滚动方向将不会产生推力不平衡力矩。因此考虑推力下降故障时，发动机推力对箭体系原点的力矩为式（8）：

3）控制力Fc及控制力矩Mc

发动机摆动会使推力产生侧向分量，该分量即为控制力Fc。控制力在箭体系中的分量形式为式（9）：

控制力对箭体系原点的力矩即为控制力矩，其在箭体系中的分量形式为式（10）～（12）：

其中，mRxj、mRzt分别为芯级和助推发动机质量；为箭体视加速度在箭体轴ox1上的投影；lRxj、lRzt分别为芯级和助推发动机质心到相应铰链轴的距离；xRxj、xRzt分别芯级和助推发动机铰链轴在纵轴上的投影点到箭体理论尖端点的距离；xT为箭体质心在纵轴上的投影点到箭体理论尖端点的距离。

4）重力G

重力在发射坐标系中三个分量为式（13）：

其中g为重力加速度；R0为地球半径；x，y，z为箭体质心在发射坐标系位置坐标。

5）气动力R和气动力矩MR

8，速度坐标系中气动力的三个分量为式（14）：

箭体系中气动力矩MR的分量形式为式（15）：

其中：α、β分别为攻角和侧滑角；αw、βw分别为由风干扰引起附加攻角和侧滑角；Cx为阻力系数，为升力系数对攻角α的导数，为侧力系数对侧滑角β 的导数；分别为箭体法向力系数对攻角和侧滑角的导数；SM为箭体特征截面积；q为速度头，当火箭高速飞行时，风速与火箭相对地球的速度相比通常很小，可近似认为火箭相对气流的速度和相对地球的速度近似相等，即V为箭体相对地球速度；xd为箭体压心在芯级纵轴上的投影点到理论尖端点的距离；ωx1、ωy1、ωz1分别为箭体转动角速度在箭体系三轴上的投影；l为箭体长度；mdx、mdy、mdz分别为相应的力矩系数。

6）发动机摆动惯性力FI和力矩MI

火箭发动机摆动时产生的侧向惯性力FI在箭体系中的分量形式为式（16）：

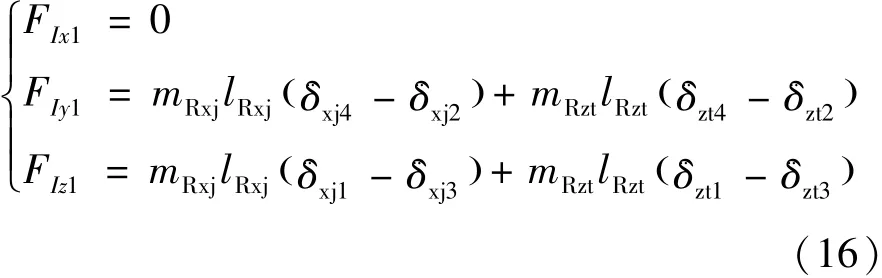
摆动惯性力矩MI在箭体系中的分量为式（17）：

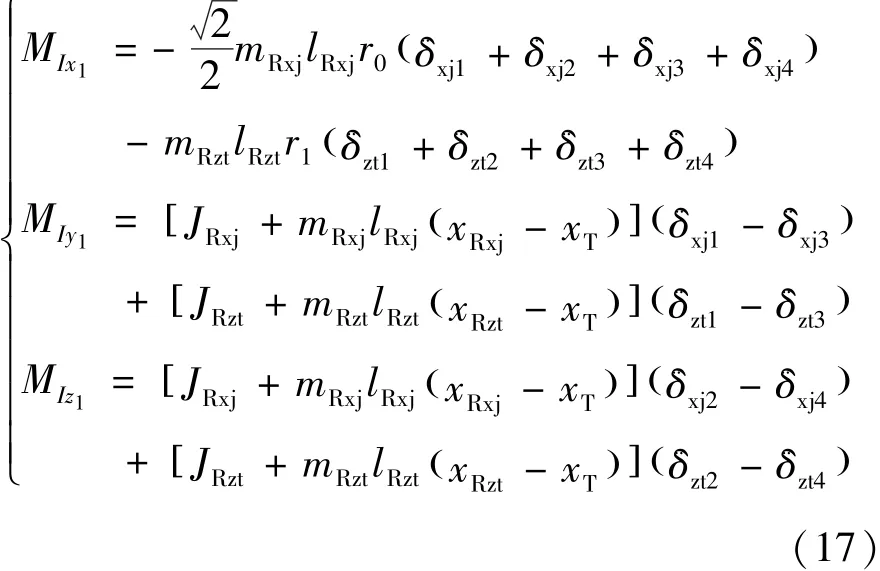
其中，JRxj、JRzt分别为芯级和助推发动机绕各自摆动中心的转动惯量。

2.2 火箭运动学方程

箭体飞行时箭体质心在发射坐标系中的坐标为（x，y，z），箭体质心相对地面的速度在发射坐标系中的投影分量记为VX、VY、VZ，则存在式（18）、（19）所示关系：

箭体绕地球转动角速度在箭体几何系中的分量为式（20）：

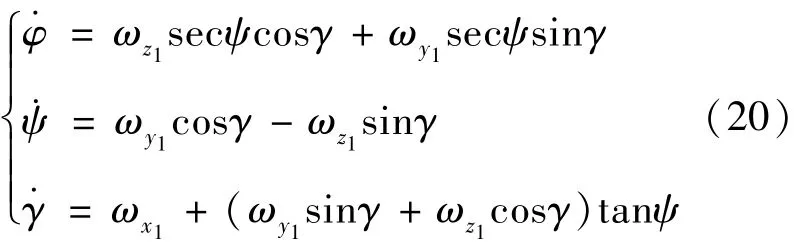
其中，φ、ψ、γ分别为箭体俯仰角、偏航角和滚动角。

2.3 欧拉角关系方程

欧拉角关系联系方程为式（21）［8］：

其中，ν为倾侧角。

3 故障仿真模型

由于推力下降可能导致箭体姿态和飞行轨迹均发生改变且引起三通道之间交联耦合，因此要分析推力下降的影响，必须基于六自由度动力学模型，综合考虑导航、制导与姿态控制，开展三通道耦合的故障仿真［10-14］。

本文基于Matlab／Simulink仿真软件，采用分层建模思想提出一种故障仿真模型，总体结构图如图3所示。系统通过惯性测量装置和角速度测量装置、导航装置完成运动参数测量和计算；根据当前速度和位置信息及预置的程序弹道产生制导信号，控制火箭质心运动，达到期望最佳终端条件时关闭助推发动机，结束助推段飞行。在飞行过程中，根据姿态角和姿态角速度产生姿控信号，进行姿态控制。

图3 故障仿真结构图Fig.3 Structure of the fault simulation system

图3 中故障火箭模块结构如图4所示，由箭体六自由度动力学模块、箭体运动学模块、发动机故障模块、偏心干扰力模块、发动机推力模块、地球重力模块、气动力模块、发动机摆动惯性力模块及总体参数模块等组成，各模块的功能如下：

1）箭体六自由度动力学模块：根据火箭所受合外力和力矩，计算箭体质心速度，视加速度和转动角速度。

2）箭体六自由度运动学模块：根据箭体质心速度和转动角速度，计算箭体质心在惯性系中的位置和相关欧拉角。

3）发动机故障模块：设置发动机故障模式并输出发动机发生故障后的推力值。

4）力与力矩模块：由重力计算模块、发动机力与力矩计算模块、气动力与力矩计算模块和干扰力与力矩计算模块组成，计算箭体所受合外力和力矩。其中，重力计算模块解算箭体所受地球重力；发动机力与力矩计算模块解算发动机推力矢量、控制力、发动机摆动惯性力及其力矩；气动力与力矩计算模块解算火箭所在空域受到的气动力及其力矩；干扰力与力矩计算模块解算结构干扰力、风干扰力及由于发动机故障导致箭体质心偏移产生的干扰力。

5）总体参数计算模块：根据燃料的消耗量实时计算发动机故障情况下运载火箭质量、惯量张量、瞬时质心相对箭体位置以及箭体飞行高度。

图4 故障火箭运动模型Fig.4 Motion model of Launch Vehicle

在Simulink中搭建的推力下降故障模块如图5所示。

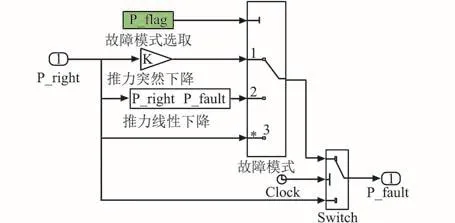
图5 故障推力模块结构图Fig.5 Thrust fault structure

4 算例验证

为验证建立仿真模型的有效性，在发动机推力正常情况下，对火箭助推飞行段进行仿真，仿真弹道数据与实际弹道数据之差如图6所示，可知仿真弹道与真实飞行弹道的姿态角偏差、速度偏差和飞行高度误差均较小，最大误差小于1.5%，因此可以认为该仿真系统可以较为真实地模拟真实飞行过程。

考虑到推力突然下降故障对运载火箭影响较大，因此本文利用建立的仿真模型，通过以下两组算例，对该故障展开讨论。

1）设定系统在运行到20 s时发生发动机推力突然下降故障。将助推1号和助推2号发动机发生关机故障两种情况对运载火箭助推段飞行的影响与正常情况进行对比，结果如图7所示。

图6 真实飞行弹道与仿真飞行弹道Fig.6 Actual flight trajectory and simulated flight trajectory

仿真运行20 s之前，发动机推力没有下降，其各项指标都没有变化。20 s之后，由图7（a）、（b）可以看出，助推1号和2号发动机发生关机故障时，运载火箭飞行高度相比正常情况降低了约60%。由（c）～（e）可以看出，助推1号和2号发动机对俯仰角的影响较小，但是助推2号发动机对偏航角影响较大，最大值达到4.5°，由于助推2号发动机推力为零，与之对称位置的助推4号发动机在偏航通道产生不平衡推力矩，箭体产生大的偏航运动，仿真结果合理。助推1号和2号发动机均使箭体产生较大的滚动角，但方向相反。

图7 推力正常与助推发动机故障下飞行参数比较Fig.7 Flight parameters in the case of booster engine failure

2）将芯级1发动机和芯级2号发动机发生关机故障两种情况对运载火箭助推段飞行的影响与正常情况进行对比，结果如图8所示。

当芯级1号和2号发动机均发生关机故障时，由图8（a）、（b）可以看出，火箭飞行高度下降了50%，沿发射坐标系X轴方向飞行距离缩短33%。由（c）～（e）可以看出，芯级1号和2号发动机推力下降对俯仰角产生影响较小，但使偏航角变大，最大偏航角达到1.7°。

5 结论

1）本文建立的发动机推力下降故障下火箭六自由度刚体动力学模型能够近似仿真模拟火箭真实飞行状态，并且利用该仿真模型，可以研究分析发动机推力下降下火箭的飞行状态；

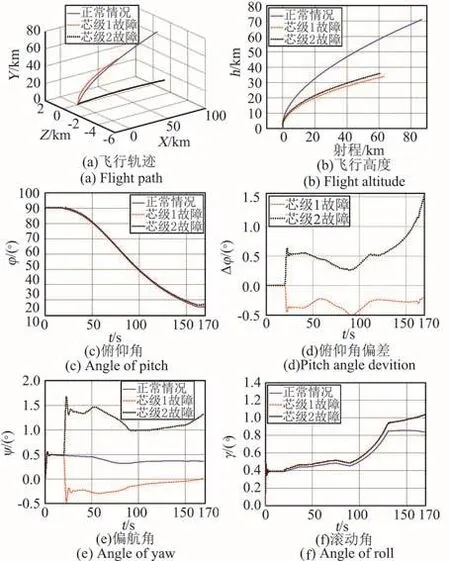
图8 芯级发动机故障与助推发动机故障下飞行参数比较Fig.8 Comparisons of flight parameters between core engine failure and booster engine failure

2）在同一特征秒时刻，不同发动机发生关机故障对运载火箭的飞行轨迹和飞行姿态影响不同。芯级发动机相对助推发动机，发生发动机关机故障时，其对运载火箭飞行轨迹和飞行姿态的影响相对较小；

3）芯级发动机和助推2号发动机发生关机故障，其飞行轨迹和飞行姿态角偏离标准弹道的程度较小；当助推1号发动机发生关机故障时，其飞行轨迹和飞行姿态角偏离标准弹道的程度较大。

参考文献（References）

［1］ 胡峰，温熙森.运载火箭动力系统突发性故障检测与辨识［J］. 航天控制，2001，19（4）：59-64.Hu Fen，Wen Xisen.Detection and recognition of burst fault in dynamical system of launch vehicle［J］.Aerospace Control，2001，19（4）：59-64.（in Chinese）

［2］ 胡珊.载人运载火箭主动段故障检测技术研究［D］.西安：西北工业大学，2005.Hu Shan.Research on Fault Detection of Launch Vehicle Boost-Phase［D］.Xian： Northwestern Poly technical University， 2005.（in Chinese）

［3］ 黄盘兴.重型运载火箭可重构控制系统设计研究［D］.哈尔滨：哈尔滨工业大学，2015.Huang Panxing.Research on Reconfigurable Control System Design of Heavy Launch Vehicle［D］.Harbin： Harbin Institute of Technology， 2005.（in Chinese）

［4］ 李新国，王文虎，王晨曦.亚轨道飞行器上升段故障模式分析与仿真［J］.飞行力学，2014，32（3）： 235-238.Li Xinguo， Wang Wenhu， Wang Chenxi.Failure mode analysis and simulation of ascent trajectory for suborbital reusable launch vehicle［J］.Flight Dynamics， 2014， 32（2）： 235-238.（in Chinese）

［5］ 程龙，蔡远文，穆利军，等.基于Matlab／Simulink的火箭飞行故障仿真［J］. 武器装备自动化，2008，27（9）：8-11.Cheng Long， Cai Yuanwen， Mu Lijun， et al.Fault simulation of launch vehicle flight based on Matlab／Simulink［J］.Armament Automation， 2008， 27（9）： 8-11.（in Chinese）

［6］ 傅维贤，张婕，卢凤翎.导弹姿态控制系统故障的数学仿真［J］.战术导弹技术， 2001（2）： 58-61.Fu Wenxian， Zhang Jie， Lu Fengling.Failure simulation of missile attitude control system［J］.Tactical Missile Technology， 2001（2）： 58-61.（in Chinese）

［7］ 李辉，敬晓刚，徐利梅.基于Matlab／Simulink的运载火箭6自由度运动仿真［J］.宇航学报，2005，26（5）：616-619.Li Hui， Jing Xiaogang， Xu Limei.Six-DOF motion simulation for launch vehicle based on Matlab／Simulink［J］.Journal of Astronautics， 2005， 26（5）： 616-619.（in Chinese）

［8］ 徐延万.液体弹道导弹与运载火箭系列——控制系统（上册）［M］.北京：宇航出版社，1989：128-129.Xu Yanwan.Liquid Ballistic Missile and Launch Vehicle—Control System（Volume One） ［M］.Beijing： Aerospace Press.1989： 128-129.（in Chinese）

［9］ 李家文.大型捆绑火箭姿态控制系统的建模、设计与分析［D］.长沙：国防科学技术大学，2011.Li Jiawen.Modeling，Design and Analysis of Large Strap-on Launch Vehicle’s Attitude Control System［D］.Changsha：National University of Defense Technology， 2011.（in Chinese）

［10］ 刘立军，徐庚保.运载火箭控制系统六自由度数字仿真研究［J］.航天控制，1998（3）：46-47.Liu Lijun，Xu Gengbao.Research on six degree of freedom digital simulation of launch vehicle control system［J］.Aerospace Control， 1998（3）： 46-47.（in Chinese）

［11］ Walker M W， Wee L B.Adaptive control of space-based robot manipulators［J］.IEEE Transactions on Robotics and Automation， 1991， 7（6）： 828-835.

［12］ Papadopoulos E G， Dubowsky S.On the nature control algorithms for free-floating space manipulators［J］.Transactions on Robotics and Automation， 1991， 7（6）：750-758.

［13］ Vava Z， Dubowsky S.On the dynamics of space manipulators using the virtual manipulator with application to path planning［J］.Journal of the Astronautical Science， 1990， 38（4）：441-472.

［14］ 阎斌，邓方林，王仕成.大型飞行器六自由度仿真建模研究［J］. 系统仿真学报，1998，10（3）：22-29.Yan Bin， Deng Fanglin， Wang Shicheng.The modeling research of six-degree-of-freedom simulation of large scale space vehicle［J］.Journal of System Simulation， 1998，10（3）： 22-29.（in Chinese）

（责任编辑：龙晋伟）

Failure Simulation of Thrust Decline of Launch Vehicle Based on Six DOF Model

WANG Zhixiang， LI Jiawen， LI Daokui
（National University of Defense Technology， College of Aerospace Science and Engineering， Changsha 410073， China）

V475

A

1674-5825（2017）05-0650-08

2016-08-15；

2017-07-31

武器装备预研项目（51320120111）

王志祥，男，硕士研究生，研究方向为运载火箭动力学建模与控制。E-mail：wangzhixiangaadt＠163.com