基于可靠性的北斗系统BCH码擦除译码算法

张超逸，刘海洋，李金海，孙金海，阎跃鹏

(1.中国科学院 微电子研究所，北京 100029; 2.中国科学院大学，北京 100049)

基于可靠性的北斗系统BCH码擦除译码算法

张超逸1,2，刘海洋1，李金海1，孙金海1，阎跃鹏1

(1.中国科学院 微电子研究所，北京 100029; 2.中国科学院大学，北京 100049)

针对北斗卫星导航系统中的BCH码译码算法性能低下问题，本文提出了一种擦除译码算法。该算法根据硬判决矢量中各个位置的可靠性，构造了一组各包含两个擦除位置的矢量。采用擦除译码算法对这些矢量进行译码，并根据一定准则选择译码结果中的一个码字作为译码输出。为了提高算法效率，设计了一种可以减少译码矢量数目的终止机制。仿真结果表明，本文设计的终止机制可以在几乎不损失性能的条件下，有效降低算法的复杂度。同传统硬判决译码算法相比，提出的算法在增加少量额外复杂度的条件下，译码性能得到改善，从而实现了在译码性能和复杂度之间的良好折中，是实际接收机的良好选择。

北斗系统； BCH码； 硬判决； 软判决； 可靠性； 擦除译码

Abstract：An efficient decoding erasure algorithm for the improvement of the decoding performance of the BCH code in the BeiDou satellite navigation system is proposed in this paper. The algorithm is used to construct a group of vectors on the basis of the reliability of each position in the hard- decision vector. Each group of vectors contains two erasure locations, and each vector is decoded by the decoding erasure algorithm. One obtained code word is selected as the output of the proposed algorithm in accordance with certain rules. To improve the efficiency of the algorithm, a termination mechanism is developed to decrease the number of decoded vectors. Simulation results show that the designed termination mechanism can effectively reduce the complexity of the proposed algorithm with little performance degradation. The proposed algorithm outperforms the traditional hard- decision decoding algorithm with a negligible increase in complexity. Therefore, the proposed algorithm achieves good tradeoff between decoding performance and complexity and is thus a good choice for practical navigation receivers.

Keywords：BeiDou system; BCH code; hard decision; soft decision; reliability; decoding erasure

目前，北斗卫星导航系统可向中国及其周边区域提供全天候的定位、导航及授时服务，北斗卫星导航接收机的设计与开发也引起了学术界和工业界的广泛兴趣[1-2]。对于卫星导航接收机而言，导航电文至关重要，其含有的卫星基本导航信息、历书信息以及与其他系统时间同步信息的准确性直接决定了接收机的定位精度。为了增强导航电文的准确性，北斗系统采用了一组循环BCH码作为导航电文的前向纠错码[3]。因此，设计该BCH码的高效译码方案具有非常重要的意义。当前北斗系统中的BCH译码算法主要分为两类：硬判决译码算法[4-5]和软判决译码算法[6-8]。硬判决译码算法具有简单、易于实现的优点，也是北斗系统接口控制文件中推荐的译码算法，但是其译码性能相对较差。针对这一问题，多种软判决译码算法被设计出来。同硬判决译码算法相比，这些算法的性能得到了改善，但由于复杂度的增加，在实现过程中往往会遇到许多困难。

除了这两类算法，擦除译码也是线性分组码(尤其是循环码)的一种重要译码算法[9-13]。可以验证，北斗系统中的BCH码最小汉明距离为3。由线性分组码的性质可知，擦除译码可以纠正包含有不超过2个擦除位置且其余位置没有错误的任意接收矢量[14]。基于上述性质，本文提出了一种北斗系统BCH码的高效译码算法。该算法将接收矢量每个位置的可靠性同硬判决矢量相结合，通过用擦除位替换掉硬判决矢量中的两个位置，构造出一组矢量。此后，对每个构造出来的矢量分别采用擦除译码算法进行译码，并根据一定准则选择译码结果中的一个码字作为译码输出。此外，为了提高算法的效率，提出了一种可以减少译码矢量数目的机制。

1 北斗系统BCH码

北斗系统中的前向纠错码采用循环BCH码，码长和信息长度分别为15和11，记为BCH(15,11)码[4]，其生成多项式为

g(x)=x4+x+1

(1)

由于该码是循环码，其编码可以通过线性移位寄存器电路有效实现[15-16]。具体编码步骤如下：

1)将待编码的信息多项式m(x)乘以xr，其中r=deg(g(x))=4。

2)用xrm(x)除以生成多项式g(x)，得到余式b(x)。

3)构造码字c(x)=b(x)+xrm(x)。

BCH(15,11)码的最小汉明距离为3，采用硬判决算法可以纠正出现在接收矢量中任意位置的单个错误。硬判决译码算法可以通过基于校正子的查找表实现，主要包括如下步骤[4]：

1)将接收矢量v除以生成多项式g,得到余式r，余式即该接收矢量对应的校正子。

2)根据校正子r查表得到相对应的错误图样e。

可以验证，BCH(15,11)码是完备码(perfect code)[14]。也就是说，对于长度为15的任意硬判决接收矢量v，在BCH(15,11)码中存在唯一的一个码字c，使得v和c之间的汉明距离不超过1。这时，用硬判决译码算法对接收矢量v进行译码得到的结果即是码字c。这种译码方式的一个缺点是当接收矢量错误数大于1时会出现译码失败。

为了解释上述现象，考虑下面的例子。假定通过信道发送码字[1 1 1 0 0 0 1 0 0 1 0 1 0 0 0]，在接收端的硬判决矢量为[1 1 1 0 1 0 1 1 0 1 0 1 0 0 0]。可以看出，接收矢量在第5和第8两个位置上出现了错误。这时通过硬判决译码算法得到的码字为[1 1 1 0 1 0 1 1 1 1 0 1 0 0 0]。同发送码字相比，译码结果出现了3个错误，比接收矢量还多出一个错误。因此，硬判决译码算法仅在信道噪声相对较低时有效，其编码增益也相对有限。

2 基于可靠性的擦除译码算法

本节提出BCH(15,11)码的一种基于可靠性的擦除译码算法，并设计了一种能提高译码算法效率的机制。

2.1 BCH(15,11)码错误概率分析

由第1节可知，任意包含有超过1个错误的接收矢量无法通过硬判决译码算法正确纠错。下面分析接收矢量中出现不同错误个数的概率。假定一个BCH(15,11)码字经过二进制相移键控(BPSK)调制后通过加性高斯白噪声(AWGN)信道传输。由文献[17]可知每个位置的错误概率为

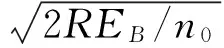
(2)

其中

(3)

式中：R=11/15为码率，Eb/N0为信噪比(SNR)。

由概率论可知[17]：

(4)

表1不同信噪比下接收矢量错误概率

Table1TheerrorprobabilitiesofareceivedvectoratdifferentSNRs

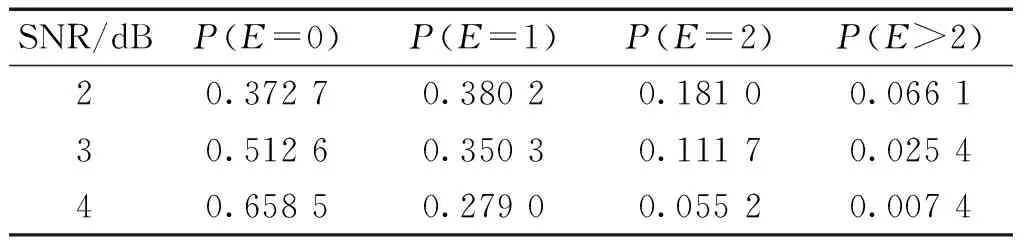
SNR/dBP(E=0)P(E=1)P(E=2)P(E>2)20.37270.38020.18100.066130.51260.35030.11170.025440.65850.27900.05520.0074

2.2 算法设计

对于最小汉明距离为dmin的BCH码，擦除译码算法可以纠正含有e个擦除位置且其余位置没有错误的所有组合，需要满足如下关系[14]：

e+1≤dmin

(5)

由于BCH(15,11)码的最小汉明距离为3，擦除译码算法可以纠正包含有2个擦除位置且其余位置没有错误的接收矢量。这说明任意包含有两个错误的硬判决矢量在准确得到其错误位置的情况下，可以通过擦除译码算法得到纠正。文献[14]中给出了擦除译码算法的主要步骤:1)通过在一个矢量的两个位置上用擦除位替换掉原先的值构造一个新的矢量；2)分别设置擦除位的值为00和11后各自采用硬判决译码算法进行两次译码，得到两个码字；3)统计这两个码字在非擦除位置上的值与之前构造出的矢量对应位置上的值相同的个数，选取相同个数多的码字作为译码结果输出。

在实际中，由于错误位置无法提前获得，从而限制了上述译码方法的应用。但是，北斗系统可以提供不同位置的可靠性信息，该信息由导航接收机中的跟踪通道实时获得。接收机完成某颗卫星的捕获后，转入跟踪状态，相应卫星的跟踪通道经过解旋、解扩、积分累加等数字信号处理算法后得到当前卫星信号上调制的数据比特观测值。这一观测值通常不是仅有两个电平0或1的硬判决量，而是可量化为具有一定位宽的多个电平值。对每个数据比特，其观测值取符号位即得到硬判决结果，而每个观测值的绝对值大小则反映了该判决的可靠性。观测值越大，表明该比特的判决结果越可靠；反之，表明判决结果越不可靠。因此，可以将可靠性信息与擦除译码相结合，设计出一种高效的译码算法。

该算法首先选择接收矢量中的L(L≥2)个不可靠位置。然后，每次选取这L个位置中的任意两个位置当作擦除位置来构造一个新的矢量。最后，对每个构造出的矢量采用上述的擦除译码算法进行译码。不难看出，构造的矢量和需要译码的矢量数目分别为N和2N，其中

(6)

为便于实现，假定N个位置按照其可靠性进行字典排序[18]。

记某个译码矢量为vk(l)，其中l=0表明擦除位被设置为00，l=1表明擦除位被设置为11，k=1,2,…,N。这2N个译码矢量依次为v1(0)、v1(1)、v2(0)、v2(1)、…、vN(0)、vN(1)，进行硬判决译码后得到2N个码字，分别为c1(0)、c1(1)、c2(0)、c2(1)、…、cN(0)、cN(1)。记符号A(ck(l),vk(l))表示在非擦除位置上ck(l)与vk(l)值相同的个数，其中k=1,2,…,N，l=0,1。算法选取A(ck(l),vk(l))具有最大值的ck(l)作为输出码字。

可以看出，译码矢量的总数2N与L的呈平方关系增加，为了减少译码矢量的个数，本文进一步设计了一种终止机制(termination mechanism, TM)。在擦除译码过程中，若错误位置正好与擦除位置一致时，那么在非擦除位置的译码结果与接收矢量应是完全相同的[14]。

四是加强监督队伍建设。“打铁还需自身硬”，推进监管体制机制的创新，需要运用信息化手段，提升监督人员业务和技术水平，使监管执法标准化、规范化，促使工程质量持续健康发展。同时应鼓励采取政府购买服务的方式，让社会力量参与监督检查活动，解决因编制受限造成监管力量不足的问题。

假定对所有2N个构造出的矢量进行顺序译码。对某一个构造出的矢量vk(l)，如果译码得到的码字ck(l)与vk(l)在所有13个非擦除位置上的值完全一致，即A(ck(l),vk(l))=13，这时认为译码输出码字为ck(l)，同时终止译码过程。这种终止机制的有效性将在下一节中通过仿真进行验证。

综上所述，基于可靠性的北斗系统BCH(15,11)码的擦除译码步骤描述如下：

输入：硬判决矢量v；每个位置的可靠性信息R；参数L。

1)根据硬判决矢量v中每个位置的可靠性信息R选择L个不可靠位置。

2)构造一组矢量vk(l)(k=1,2,…,N;l=0,1)。

3)对这些构造出来的矢量顺序地进行硬判决译码，得到译码码字ck(l)。

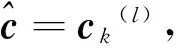
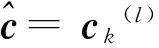
2.3 复杂度分析

基于可靠性的北斗系统BCH(15，11)码的擦除译码算法的复杂度主要集中在步骤1)到步骤3)。在步骤1)中，找到L个不可靠位置需要进行15L次比较。在步骤3)中，复杂度正比于译码矢量的平均数目。通常情况下译码矢量数目为L(L-1)，但应用设计的终止机制后，能有效减少译码矢量的数目。在下一节可以看到，在合适的信噪比范围内，采用终止机制后的平均译码矢量的数目很少。例如，当L=4时，算法中的译码矢量数目不会超过2个，同传统的硬判决译码算法相比较，本文提出的算法仅多增加60次比较操作和1次硬判决译码操作，因此该算法具有低复杂度的优点。

3 仿真结果及分析

通过仿真确定参数L的取值，并评估设计的终止机制。仿真中每个位置上的可靠性信息采取6 bit均匀量化[17]。为了进行比较，本文同时仿真了北斗系统接口控制文件中推荐的硬判决译码算法和文献[8]中的最大似然软判决译码算法的译码性能。

图1给出了参数L取不同值时，提出的基于可靠性的擦除译码算法的性能。从图1中可以看出，提出的译码算法的性能随着L取值的增加而获得改善。特别地，当L=4时算法的性能相对于L=2和L=3时的性能有较大改善，而当L=5时算法的性能相对于L=4时的性能改善相对较小。因此，在实际中建议参数L取值为4。

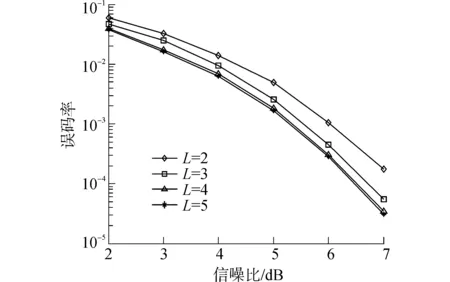
图1 提出的译码算法在L=2,3,4,5时的性能比较Fig.1 Performance comparisons of the proposed algorithm if L=2,3,4,5

图2对比了BCH(15,11)码采用不同译码算法的性能。

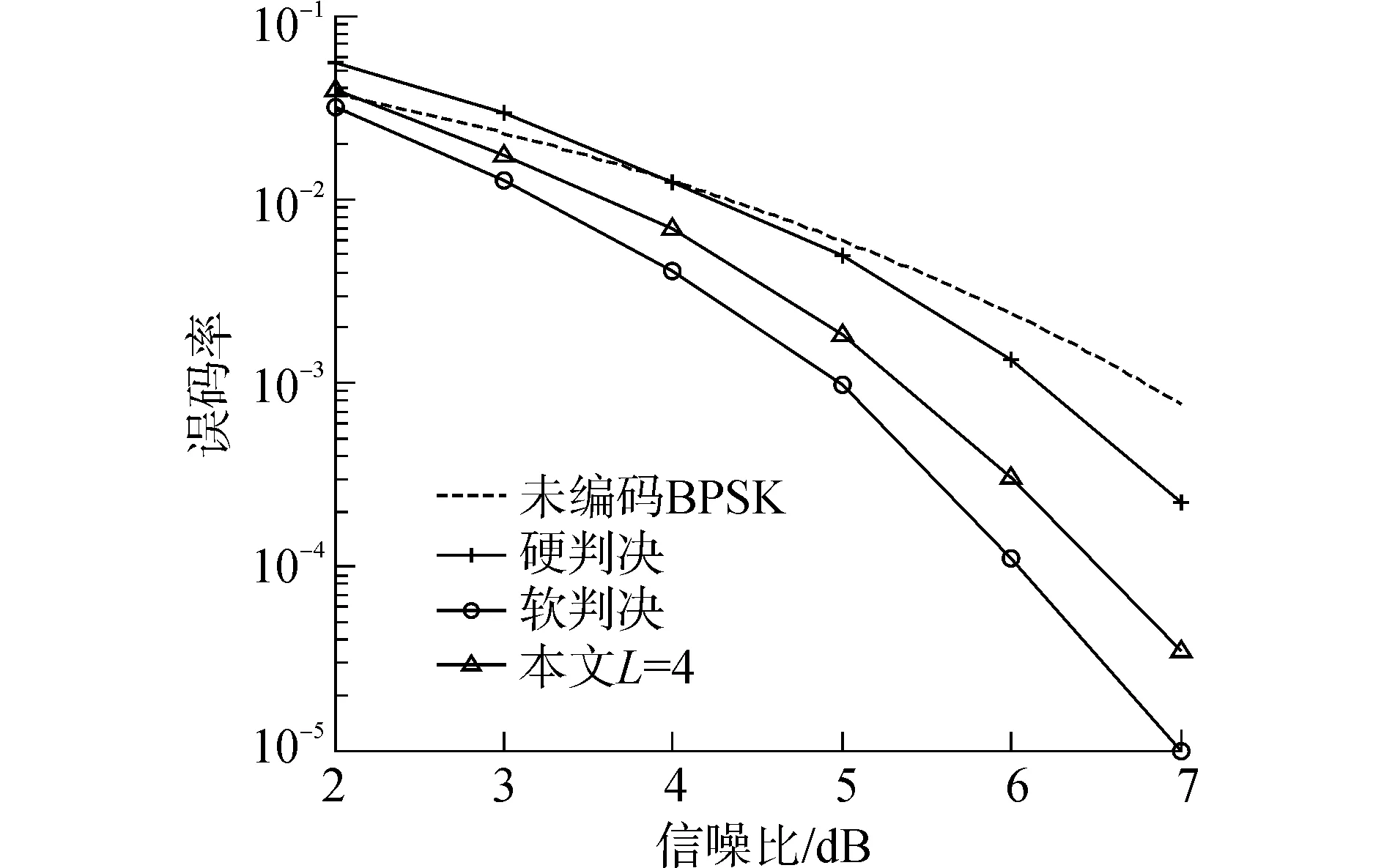
图2 BCH(15,11)码采用不同译码算法的性能Fig.2 Performances of BCH(15,11) code under different decoding algorithms

可以看出，本文提出的算法译码性能明显优于传统的硬判决译码算法。例如，对任意的译码算法，总会存在一个编码阈值，当低于这个阈值时，编码无效。对于实际系统，应当设计译码算法，使得编码阈值尽量地低[18-19]。由图2中可以看出，本文提出的算法相对于传统硬判决译码算法的编码阈值性能得到了改善。如传统的硬判决译码算法的编码阈值约为4 dB，而当选取L=4时本文提出的算法的编码阈值约为2.2 dB。

为了提供首次定位服务，要求导航电文的误比特率必须小于10-3[20]。从图2中可以看出，在满足误比特率小于10-3条件下，当选取L=4时，提出的算法同传统的硬判决译码算法和未编码BPSK相比，性能分别提升0.8 dB和1.8 dB左右。

另外，本文提出的算法在性能上接近最大似然软判决译码算法(即在BCH(15,11)码中选择码字c，使得内积的值最大，其中r为接收软判决向量)。从图2中可以看出，当L=4时，误比特率为10-3，本文的算法同最大似然软判决算法之间性能差距小于0.5 dB。但是，最大似然软判决译码算法非常复杂。由于BCH(15,11)码包含2 048个码字，因此若采用直接实现，需要约2 048×(15-1)=28 672次加法操作和2 047次比较操作。文献[8]中的给出了BCH(15,11)码最大似然软判决译码的一种有效实现方案。若采用该方案，也至少需要额外的240次加法操作和135次比较操作。与此相比，本文提出的译码算法基于硬判决译码实现，仅需要增加少量的逻辑运算。

图3对比了采用终止机制和不采用终止机制时提出的译码算法的性能。从图中可以看出，采用了终止机制后，算法的性能几乎没有任何损失。表2给出了在不同信噪比下的译码矢量的平均数目。可以看出，提出的算法的译码矢量的平均数目不多，并且随着信噪比的提高，译码矢量的平均数目减少。这说明了采用终止机制后算法的平均复杂度会很低，从而验证了终止机制的有效性。

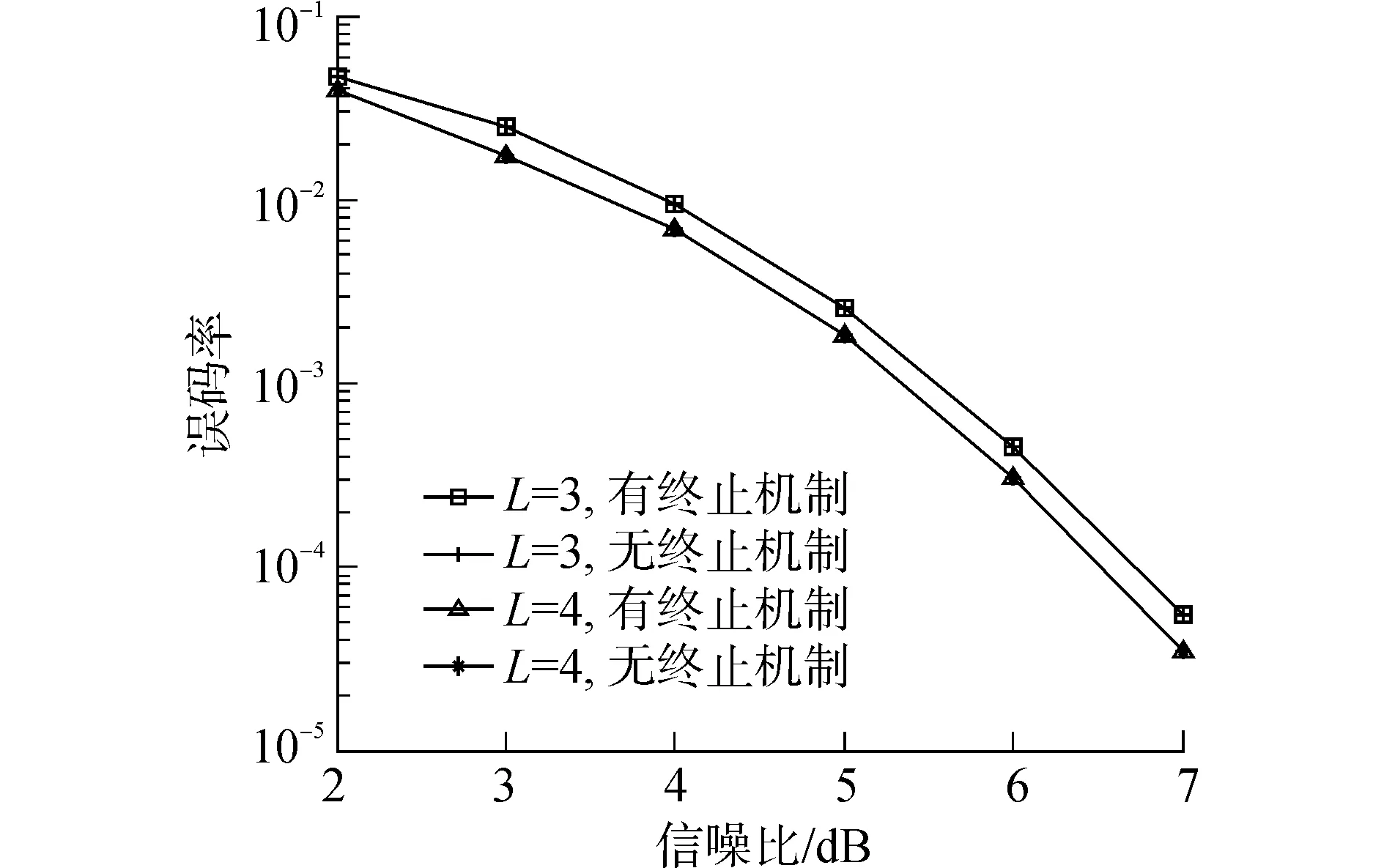
图3 提出的终止机制的性能评估Fig.3 Performance evaluation for the proposed TM

综上所述，本文提出的基于可靠性的擦除译码算法是实际导航接收机的良好选择。

表2不同信噪比下译码矢量平均数目

Table2TheaveragenumberofdecodedvectorsunderdifferentSNRs

LSNR/dB23456732.2701.8271.4711.2991.2391.22842.8662.1191.5821.3271.2431.229

4 结论

1)基于可靠性的高效擦除译码算法在增加少量复杂度的基础上能明显改善译码性能，避免了传统硬判决译码算法性能相对较差以及软判决译码算法复杂度高的缺点。

2)对算法的参数L进行了仿真，结果表明L取4时能最大程度平衡性能提升与复杂度增加之间的矛盾，是一个合理的选择。

3)本文提出的译码算法在性能上同传统的硬判决译码算法和未编码BPSK相比有明显提升，同最大似然软判决译码算法相比性能接近。

4)提出了一种译码算法终止机制，使得在算法性能几乎没有任何损失的条件下有效减少译码矢量数目。

5)复杂度分析表明，本文提出的算法操作简单，易于通过软硬件加以实现，非常适合在北斗系统导航接收机(特别是低成本接收机)中应用。

[1] 中国卫星导航系统管理办公室. 北斗卫星导航系统发展报告[J]. 国际太空, 2012(4): 6-11. China satellite navigation office. Report on the development of BeiDou navigation satellite system[J]. Space international, 2012(4): 6-11.

[2] 吴海玲, 高丽峰, 汪陶胜, 等. 北斗卫星导航系统发展与应用[J]. 导航定位学报, 2015, 3(2): 1-6. WU Hailing, GAO Lifeng, WANG Taosheng, et al. Development and application of Beidou navigation satellite system[J]. Journal of navigation and positioning, 2015, 3(2): 1-6.

[3] 王迪, 郝士琦, 朱斌. “北斗”2代B1I信号导航电文分析[J]. 航天电子对抗, 2013, 29(6): 30-32. WANG Di, HAO Shiqi, ZHU Bin. Analysis for navigation message of BeiDouII B1I signal[J]. Aerospace electronic warfare, 2013, 29(6): 30-32.

[4] 中国卫星导航系统管理办公室． 北斗卫星导航系统空间信号接口控制文件公开服务信号B1I[EB/OL]. [2013-12-27]. http://www.beidou.gov.cn. China satellite navigation office. BeiDou navigation satellite system signal in space interface control document[EB/OL]. [2013-12-27]. http://www.beidou.gov.cn.

[5] MEGGITT J E. Error correction codes and their implementation for data transmission systems[J]. IEEE transactions on information theory, 1961, 7(4): 232-244.

[6] VARDY A, BEERY Y. Maximum- likelihood soft decision decoding of BCH codes[J]. IEEE transactions on information theory, 1994, 40(2): 546-554.

[7] MULLER B, HOLTERS M, ZOLZER U. Low complexity soft- input soft- output hamming decoder[C]//FITCE congress, Italy, 2011: 1-5.

[8] SUN J, LI J, LIU H, et al. Efficient soft- decision maximum- likelihood decoding of BCH code in the GNSS[J]. Journal of Harbin Institute of Technology (New Series), 2015, 22(1): 54-58.

[9] STEVENS P. Error- erasure decoding of binary cyclic codes, up to a particular instance of the Hartmann- Tzeng bound[J]. IEEE transactions on information theory, 1990, 36(5): 1144-1149.

[10] SHAHRI H, TZENG K K. On error- and- erasure decoding of cyclic codes[J]. IEEE transactions on information theory, 1992, 38(2): 489-496.

[11] LIVA G, PAOLINI E, MATUZ B, et al. A decoding algorithm for LDPC codes over erasure channels with sporadic errors[C]//2010 48th Annual Allerton conference on communication, control, and computing, Allerton, 2010: 458-465.

[12] SONG S, LIN S, ABDEL K, et al. Burst decoding of cyclic codes based on circulant parity- check matrices[J]. IEEE transactions on information theory, 2010, 56(3): 1038-1047.

[13] PAOLINI E, LIVA G, MATUZ B, et al. Maximum likelihood erasure decoding of LDPC codes: pivoting algorithms and code design[J]. IEEE transactions on communications, 2012, 60(11): 3209-3220.

[14] MACWILLIAMS F J, SLOANE N J A. The theory of error correcting codes[M]. Amsterdam: North- Hooland publishing company, 1977: 185-186.

[15] 张彦, 李署坚, 崔金. 一种BCH码编译码器的设计与实现[J]. 通信技术, 2010, 43(12): 24-25+186. ZHANG Yan, LI Shujian, CUI Jin. Design and implementation of BCH encoder/decoder[J]. Communications technology, 2010, 43(12): 24-25+186.

[16] PETERSON W W. Encoding and error- correction procedures for the Bose- Chaudhuri codes[J]. IEEE transactions on information theory, 1960, 6(4): 459-470.

[17] PROAKIS J G. Digital communications[M]. 5th. New York: mcgraw- hill, 2007.

[18] LEISERSON C C E, RIVEST R R L, STEIN C, et al. Introduction to algorithms[M]. 3rd Ed. Massachuseus: MIT press and mcgraw- hill, 2009: 118-118.

[19] LIN S, COSTELLO D J. Error control coding: fundamentals and applications[M]. 2nd ed. Englewood Cliffs, NJ, USA: Prentice- Hall, 2004.

[20] KAPLAN E D, HEGARTY C J. Understanding GPS: principles and applications[M]. 2nd ed. Norwood, MA: Artech House, Inc, 2006.

Reliability-baseddecodingerasurealgorithmforBCHcodeintheBeiDousystem

ZHANG Chaoyi1,2, LIU Haiyang1, LI Jinhai1, SUN Jinhai1, YAN Yuepeng1

(1.Institute of Microelectronics, Chinese Academy of Sciences, Beijing 100029, China; 2.University of Chinese Academy of Sciences, Beijing 100049, China)

10.11990/jheu.201605010

http://www.cnki.net/kcms/detail/23.1390.u.20170427.1510.064.html

TN911.22

A

1006- 7043(2017)09- 1426- 05

2016-05-05. < class="emphasis_bold">网络出版日期

日期：2017-04-27.

国家自然科学基金项目(61271423).

张超逸(1990-), 男,博士研究生; 阎跃鹏(1964-), 男,研究员,博士生导师.

张超逸，E- mail: zhangchaoyi@ime.ac.cn.

本文引用格式：张超逸，刘海洋，李金海，等. 基于可靠性的北斗系统BCH码擦除译码算法[J]. 哈尔滨工程大学学报， 2017， 38(9): 1426-1430.

ZHANG Chaoyi, LIU Haiyang, LI Jinhai, et al. Reliability- based decoding erasure algorithm for BCH code in the BeiDou system[J]. Journal of Harbin Engineering University， 2017， 38(9): 1426-1430.