塑壳断路器操作机构结构与受力分析

熊劲华++王兴利++葛世伟

摘 要：为了确定操作机构具有确定运动的条件，绘制出了运动简图，并计算在不同状态时的自由度；为了直观了解操作机构在某些特定位置的受力状况，采用图解法对操作机构进行受力分析。

关键词：塑壳断路器；操作机构；运动简图；图解法；受力分析

中图分类号：TM561 文献标志码：A 文章编号：2095-2945（2017）29-0064-03

Abstract： In order todetermine the condition that aoperating mechanism has definite motion， this paper plotted the motion diagram of operating mechanism， and calculated the freedom of in different states.In order to visually understand the force of operating mechanism in certain position， this paper carried out force analysisof operating mechanism using graphic method.

Keywords： MCCB； operating mechanism； motion diagram； graphic method； Force analysis

引言

操作机构连接触头系统，通过运动实现塑壳断路器对电路的闭合和开断操作[1]。近年来，国内外优秀企业不断推出功能齐全、性能稳定的新产品，这就需要对操作机构作进一步的研究与分析。文献[2]通过仿真分析了塑壳断路器操作机构主拉簧刚度、关键轴位置、各杆件质量及连杆位置转换对机构运动速度的影响；文献[3]利用多体动力学仿真软件ADMAS建立了机构的分析模型，对塑壳断路器的分闸、合闸过程进行了仿真分析。本文通过对操作机构运动简图的绘制，计算出塑壳断路器在不同状态时的自由度，确定连杆机构具有确定运动的条件；运用图解法对操作机构进行受力分析，并对分析结果进行验证。

1 塑壳断路器操作机构的结构分析

1.1 操作机构的运动简图

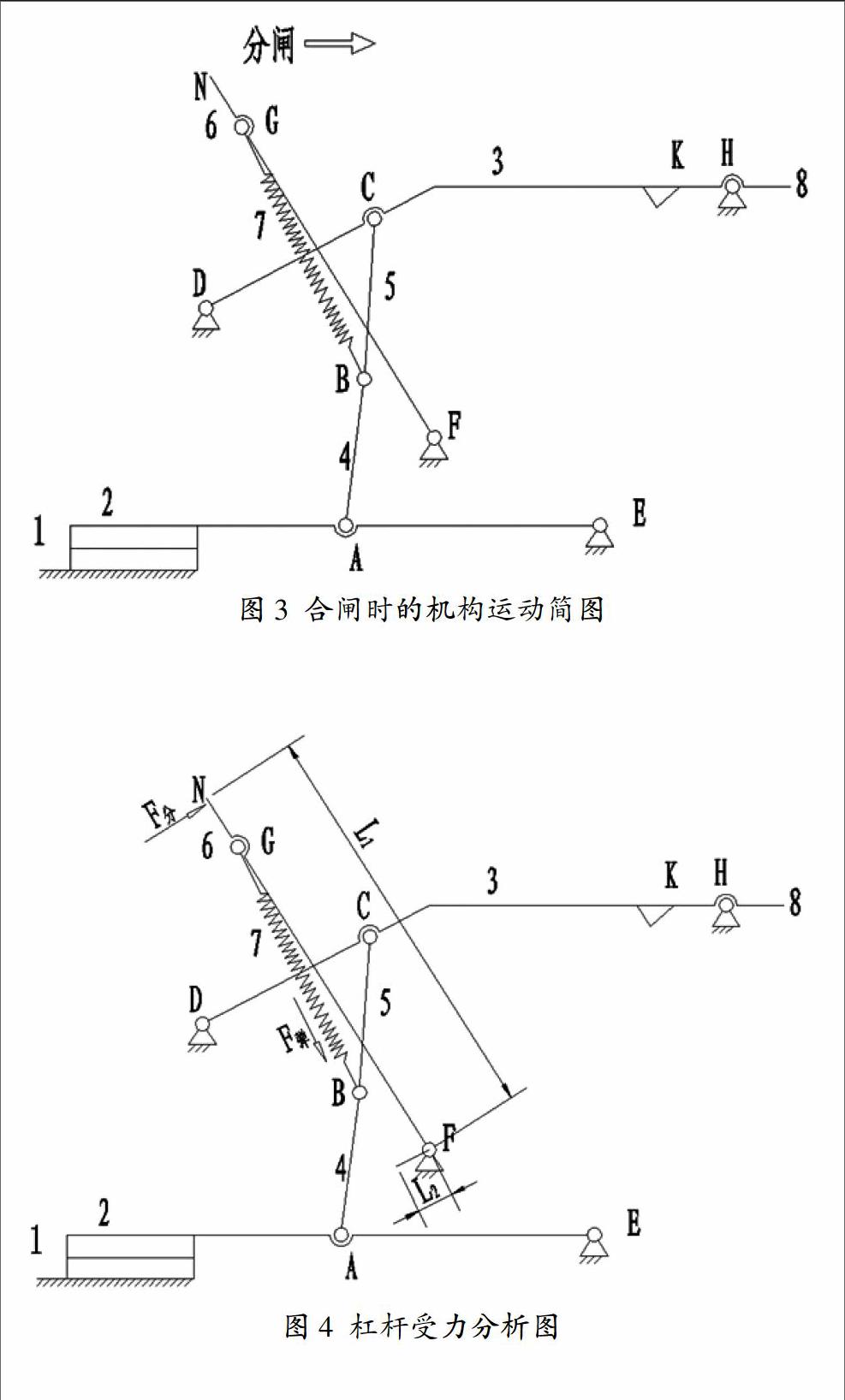
塑壳断路器的闭合与断开都是由操作机构来实现，而操作机构实质上是一种连杆机构。无论对现有塑壳断路器进行分析或设计新的操作机构，都需要绘制出机构运动简图[4]。塑壳断路器处于自由脱扣状态时的机构运动简图如图1所示，处于分闸再扣状态时的机构运动简图如图2所示，处于完全合闸状态时的机构运动简图如图3所示。

在三个机构运动简图中，构件1表示静触头，构件2表示动触头，构件3表示跳扣，构件4表示下连杆，构件5表示上连杆，构件6表示杠杆，构件7表示主拉簧，构件8表示锁扣。点A为铰接点，形成转动副A；点B为铰接点，形成转动副B；点C为铰接点，形成转动副C；点D为支撑固定铰接点，形成转动副D；点E为支撑固定铰接点，形成转动副E；点F为支撑固定铰接点，形成转动副F；点H为支撑固定铰接点，形成转动副H；点K为接触点，形成平面高副K；点N为外力施加在构件6上的作用点。

如图1所示，由构件2、构件4、构件5、构件3、铰接点E及铰接点D构成一个平面五连杆机构；如图2、图3所示，因构件3被构件8锁死，故两构件可视为固定不动件。由构件2、构件4、构件5、铰接点E及铰接点C构成一个平面四连杆机构。

1.2 塑壳断路器操作机构自由度的计算

1.2.1 平面五连杆机构自由度的计算

如图1所示，塑壳断路器在自由脱扣状态时形成的平面五连杆机构的活动构件为构件2、构件3、构件4、构件5、构件6、构件7，活动构件数量n=6。转动副A、转动副C、转动副D、转动副E、转动副F、转动G都为简单铰链，而转动副B为复合铰链，因此低副的数量pl=8。因为该平面五连杆机构都是铰链连接，故没有高副（高副数量ph=0）。

机构的自由度F满足以下关系式：

F=3n-（2pl+ph）=3×6-（2×8+0）=2

因为该平面五连杆机构的自由度F=2，故操作机构只能实现围绕固定点D向前、向后两个动作。

1.2.2 平面四连杆机构自由度的计算

如图2、图3所示，自由脱扣后再扣和合闸状态时形成的平面四连杆机构的活动构件为构件2、构件4、构件5、构件6、构件7，活动构件数量n=5，转动副A、转动副E、转动副F、转动副C、转动副G为简单铰链，而转动副B为复合铰链，因此低副的数量pl=7。因为该平面四连杆机构都是铰链连接，故没有高副（高副数量ph=0）。

机构的自由度F满足以下关系式：

F=3n-（2pl+ph）=3×5-（2×7-0）=1

因为平面四连杆机构的自由度F=1，故操作机构只能实现一种动作，即合闸（图2所示）、分闸（图3所示）。

2 塑壳断路器操作机构受力分析

2.1 操作机构杠杆受力分析

塑壳断路器完全合闸后，即将分闸操作时，以杠杆为研究对象，以点F为力偶作用点，受力分析如图4所示。

图4 杠杆受力分析图

图4中，F分为杠杆在N点受到的外力，F弹为拉簧在G点作用在杠杆上的拉力，L1为力F分到点F的距离，L2为力F弹到点F的距离。因为两力在点F形成力偶平衡，所以得到以下关系式：

F分×L1=F弹×L2（1）

2.2 操作机构动触头受力分析

塑壳断路器处于完全合闸状态时，以动触头为研究对象，以点E为力偶作用点，受力分析如图5所示。

图5 动触头受力分析图

图5中，F终为静触头施加给动触头的作用力，FBA为下连杆施加给动触头的作用力，L3为F终至点E的距离，L4为FBA至点E的距离。两力在点E形成力偶平衡，得到如下关系式：

3×F终×L3=FBA×L4（三極断路器）（2）

2.3 操作机构上连杆受力分析

塑壳断路器处于完全合闸状态时，以上连杆为研究对象，以点B为力的作用点，受力分析如图6所示。

图6 上连杆受力分析图

图6中，F弹为拉簧对上连杆的拉力，FAB为下连杆施加给上连杆的作用力，FCB为跳扣对上连杆的作用力，a为合闸角。三力汇交于点B，且塑壳断路器处于完全合闸状态时，上连杆与下连杆几乎成一条直线。

由图6知，上连杆的受力关系如下：

FCB=FAB+F弹×cosa（3）

2.4 操作机构跳扣受力分析

塑壳断路器处于完全合闸状态时，以跳扣为研究对象，以点D为力的作用点，受力分析如图7所示。

图7中，FBC为上连杆对跳扣的作用力，FK为锁扣在接触点K对跳扣的作用力，L5为FK到D点的距离，L6为FBC到D点的距离。跳扣在D点处于力偶平衡状态得到：

FBC×L6=FK×L5（4）

综合（1）、（2）、（3）、（4）得到：

FK=3×F终×■+F分×cosa×■（5）

3 结束语

本文从机械原理的角度，根据操作机构再扣、合闸、分闸的状态，解释了其具有确定运动的原因，分析了关键部件的受力状况，为现有操作机构的优化和新机构的设计提供了理论参考与经验借鉴。

参考文献：

[1]孙吉升，施政，顾惠民.塑壳断路器操作机构动作分析与设计要点[J].低压电器，2013（21）：13-15.

[2]蒋顾平，顾惠民.提高塑壳断路器操作机构动作速度的研究[J].电器与能效管理技术，2015（1）：21-23.

[3]张波，陈德桂.旋转双断点塑料外壳式断路器机构的动态仿真及优化[J].低压电器，2007（13）：5-7.

[4]孙恒，陈作模，葛文杰.机械原理[M].北京：高等教育出版社，2006.endprint