基于变分理论的局部自适应高保真图像去噪算法

钱 伟，刘 谦，陈兰英

(中国民用航空飞行学院 飞机修理厂，四川 广汉 618307)

基于变分理论的局部自适应高保真图像去噪算法

钱 伟，刘 谦，陈兰英

(中国民用航空飞行学院 飞机修理厂，四川 广汉 618307)

针对现有的图像去噪模型不能很好保留图像边缘及纹理的缺点，在变分理论的基础上提出了改进的局部自适应图像去噪算法，该算法基于图像局部特性计算保真参数，利用小波变换进行噪声方差估计，采用小的自适应窗确定保真参数，并利用该高保真去噪算法对叠加高斯噪声的图像进行了降噪处理，结果显示比全局变分采用最速下降自动选择保真参数的去噪效果要好，峰值信噪比(PSNR)在不同高斯噪声背景下都有0.2-0.5dB的提升。

图像去噪；变分理论；小波变换；局部自适应

0 引言

去噪是图像还原中的必要过程，但图像在降噪的过程中，其边缘、细节、纹理和轮廓等重要信息不可避免会受到平滑，因而不同程度地导致图像模糊。普通的线性方法和非线性方法不能解决去噪与保留图像细节和纹理之间的矛盾，而基于偏微分方程的变分模型因为良好的性能，为解决这对矛盾提供了可能[1-2]。目前基于偏微分方程理论的去噪方法已被成功地应用于图像处理中，一类经典的去噪模型就是总变分模型，该方法能够保留图像边缘，因此受到广大学者青睐，普通的传统全变分TV去噪方法虽然能够很好地去除噪声，但对图像中一些重要的信息，如细节和纹理信息不能很好地保留，特别是在处理纹理丰富或较丰富的图像时，易丢失重要信息[3]。对此，Guy Gilboa等人提出了一种基于总变分的高效保留图像纹理和细节的方法[4]，根据残差得到其局部能量，并认为这是噪声方差的近似，然而图像中边缘和细节总是具有突变性，因此这种保真方法在去噪的同时势必造成图像的模糊，影响图像的质量。本文提出了一种改进的能保留图像细节和纹理的高保真去噪算法，通过基于图像局部特性计算保真参数，采用小的自适应窗，在小的自适应窗下确定保真参数，从而实现局部图像信息的自适应保真参数选择，使图像在降噪的同时，保留图像的细节和纹理。不仅能改善去噪后图像的视觉效果，而且有利于对图像的后续处理。

1 基于变分法的去噪模型

变分法的基本思想是将去噪问题归结为一个泛函最小化问题，然后求出相应的偏微分方程，再数值求解。在基于偏微分方程的模型中，Rudin、Osher和Fatemi[5]在1992年提出的变分极小化模型，TV是经典的去噪模型之一，该算法是在图像的能量泛函中找平衡态，即求最小化能量ETV：

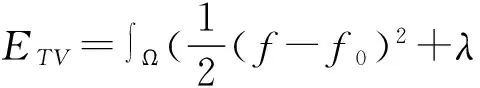
(1)

式中，f表示去噪后的图像，Ω表示图像区域；f0为带噪的观测图像；f=(fx,fy)T，表示在坐标(x,y)处的梯度，|f|表示梯度的模，λ为大于0的正则化参数。 等式中的第一项为保真项又称为逼近项，控制着图像f和观测图像f0间的差异；等式右端第二项称为正则项，为图像f的总变分TV范数，它依赖于图像的边缘，正则项在TV模型中起到很重要的作用，它使得图像中可以有不连续的部分，但不允许振荡存在，λ在正则项和保真项中起平衡作用。因此基于总变分模型的方法能够有效地去除噪声并保留图像细节和纹理。

利用变分理论，最小化ETV问题转化为求解带有Neumann边界条件的Euler-Lagrang方程：

(2)

式中，∂Ω为图像的边界，n为边界∂Ω处的单位外法向量，div(·)表示散度，其它符号的意义同上。函数φ(|f|)的选择对图像处理的影响很大，要求函数φ(t)在图像连续区域，即|f|较少的区域，应该有大的平滑；在棱边附近，|f|很大。为了保存棱边，要求平滑系数在梯度方向η方向上减少到0，比梯度正交的方向ξ方向上减少要快。即要求φ(t)满足：

(3)

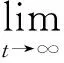
(4)

2 高保真参数估计

2.1 噪声估计

本文选用高斯白噪声模型来逼近实际中的噪声模型，根据Euler-Lagrang方程求解λ，此时参数λ可以表示为：

(5)

式中，σ2表示噪声方差，|Ω|表示图像的面积。即参数λ的选择和噪声方差σ2有关，但实际中图像的噪声方差往往是未知的，因此要实现自动保真参数选择，必须有一种鲁棒的自适应强的噪声方差估计方法，否则不能保证参数λ的合理选择。目前学者们针对噪声方差的估计提出了诸多方法[6-8]，这些方法一般可分为两类，一类是基于概率统计的方法，这类方法具有一定的适用性，但对细节和纹理较丰富的图像来说，方法误差大，因此不具有普适性；另一类是基于小波理论的噪声估计方法，该方法根据图像的噪声主要存在于高频部分这一特点，对高频部分HH的小波系数yi取模，并取其中位数做为图像噪声方差的估计。本文选用基于小波理论的噪声估计方法，并改进计算公式估计方差：

(6)

因高频部分HH的个数为偶数，所以其中值取中间两个数的平均值。median(·)是一个求平均值的函数，abs(·)是一个取绝对值的函数。

2.2 自适应高保真的参数选择机理

变分法处理后的图像与原图相比都存在不同程度的模糊，图像清晰度降低，其原因在于保真项中的参数是基于全局的。要使图像在降噪的同时，保留图像的细节和纹理，就要求对图像细节和边缘部分有小的平滑，这就要求其保真项中的保真参数必须基于图像局部特性。为了实现局部图像信息的自适应保真参数选择，一个简单的基本想法是采用小的自适应窗，在这个小的自适应窗下根据式(5)确定保真参数。

设选择的自适应窗口大小为Ω1，窗口的中心位置在(x,y)处，则式(5)可以表述为：

(7)

其中，f-f0得到的图像的残差Ir，而图像的残差主要由图像的纹理、细节、边缘、噪声构成。为了降低噪声对保真系数的影响，可以将普通窗换成高斯窗，因为高斯函数有好的光滑性，从而可以减少噪声对参数的影响。设窗口的大小为Ω，即整个图像，Ω1以外的区域值为0。

设wx,y(x1,y1)=w(|x-x1|,|y-y1|)是一个以(x,y)为中心的标准的高斯分布函数。则式(7)可以表示为：

(8)

设残差

Ir=f-f0,

(9)

定义残差的局部能量P，

(10)

则式(8)可以写为

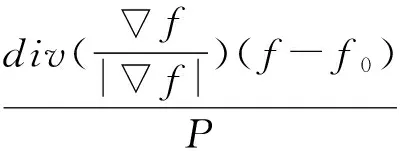
(11)

3 算法实现及验证

3.1 自适应高保真去噪算法

输入参数：噪声图像

输出图像：去噪图像

步骤1：估计噪声方差：对含噪图像进行小波分解，估计其噪声标准差，本文采用Harr小波；

步骤2：求解残差的局部能量

1)初始化λ=0、f=f0、步长dt、迭代次数iter、容差tol，本文取dt=0.2，iter=10，tol= 0.01;

2)对含噪图像利用最速下降法求解最优的原始图像的估计：

while(mean(mean(‖f-f0‖))≤tol)；

利用最速下降法实现图像降噪；

调用降噪后图像完成保真参数的自动选择；

End while.

3)计算残差Ir；

4)计算残差的局部能量P。

步骤3：实现高保真的自适应去噪

1)初始化矩阵λ为0矩阵、f=f0、步长dt、迭代次数iter、容差tol，本文取dt=0.2，iter=10，tol= 0.001;

2)利用最速下降法求解最优的原始图像的估计：

while(mean(mean(‖f-f0‖))≤tol);

利用最速下降法实现图像降噪;

利用式(8)计算保真参数矩阵λ；

End while.

步骤4：结束。

3.2 实验仿真验证

基于上述高保真去噪算法对加了高斯噪声的图像进行了降噪处理，结果发现本文提出的方法比全局采用最速下降保真参数自动选择的去噪效果要好，不易使图像模糊，细节和纹理特征能够得到更好地保留。

图1 原始灰度图像

图1是用于加噪的原始灰度图像，给该原始图像分别加上标准方差分别为5、10、15、20的高斯白噪声，图像的峰值信噪比(PSNR)分别为33.192dB、27.256dB、23.686dB、21.897dB，其相应的加噪图像及处理图像见表1。从表1中可以看出，全局保真参数的去噪方法在保护图像细节和纹理方面较差，致使图像清晰度大大降低；本文的方法在保留细节和纹理方面有所提高。为了定量地描述图像质量的改善，采用峰值信噪比对三种方法进行了比较，其结果见表2。从表2可以看出本文的方法改善信噪比最多，这也表明本文方法性能优于全局保真降噪算法。

4 结语

本文针对高斯噪声模型，首先分析了变分去噪模型的去噪机理，然后介绍了全局保真参数选择的机理和相应的去噪方法，针对确定全局保真参数要求准确知道噪声方差这一特点，提出了一种改进的基于小波变换的噪声方差估计方法，通过对高保真的参数选择机理进行推理和分析，提出一种基于局部保真的去噪算法，最后的仿真实验结果证明本文所提的高保真方法在去噪的同时，能很好地保护图像细节和纹理。在不同的噪声背景下，计算得到的峰值信噪比均比全局保真算法高出0.2-0.5dB。

表1 本文方法和全局保真参数去噪效果比较

续表1

加噪图像本文方法全局保真参数去噪噪声标准方差15噪声标准方差20

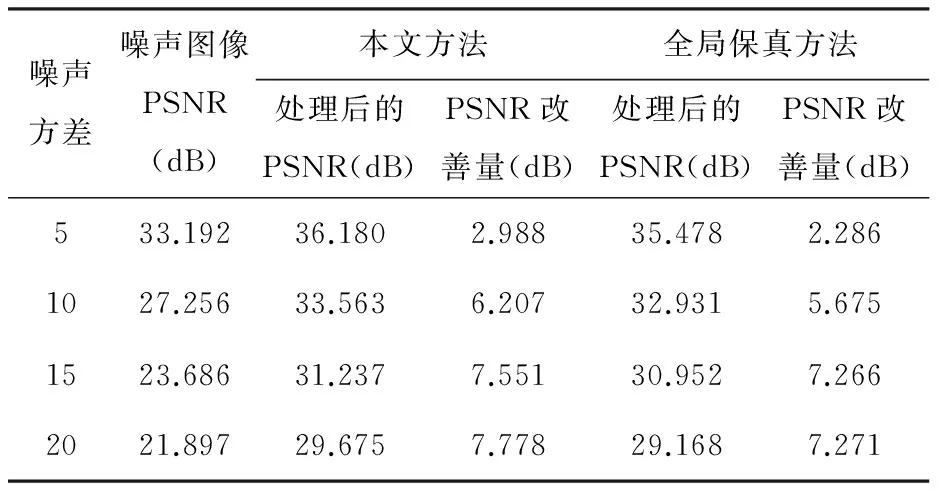
表2 本文方法与全局保真方法比对

[1] 马瑜,赵九龙,李振兴,等.三维图像分数阶微积分去噪增强算法[J].计算机工程与设计,2015,36(6):1586-1591.

[2] 于欣妍,王亮,罗四维.基于微分流形的图像复原方法[J].北京交通大学学报,2015,39(5):1-8.

[3] 杨燕,金正猛,蒋晓连,等.保持泊松噪声图像细节的快速变分去噪算法[J].计算机工程与应用,2016,52(20):172-176.

[4] GILBOA G,ZEEVI Y Y,SOCHEN N.Texture Preserving Variational Denoising Using an Adaptive Fidelity Term [J].Proceedings of the Workshop on Variational and Level Set Methods(VLSM),2003(3):8.DOI:10.1.1.116.3593.

[5] RUDIN L I,OSHER S,FATEMI E.Nonlinear Total Variation based Noise Removal Algorithms [J].Physica D:Nonlinear Phenomena,1992,60(1-4):259-268.

[6] 张旭升,周桃庚,沙定国.数字图像噪声估计的方法及数学模型[J].光学技术,2005,31(5):719-722.

[7] 杨涛,方帅,程文娟.基于熵的图像噪声方差估计[J].中国科学技术大学学报,2015,45(4):337-344.

[8] 方帅,夏秀山,曹洋,等.基于噪声水平估计的图像盲去噪[J].模式识别与人工智能,2015,28(1):50-58.

[责任编辑、校对：郝杰]

Abstract：To solve the problem that the existing image denoising model can not preserve the image edge and image texture,an improved local adaptive image denoising algorithm based on the traditional variable theory was proposed.The algorithm calculates high-fidelity(Hi-Fi)parameters on the basis of local image features,estimates noise variance via wavelet transform,and determines high-fidelity (Hi-Fi) parameters with a smaller adaptive window.A image with Gauss noise was processed through this high-fidelity denoising algorithm,and the results show that the method proposed in this paper is able to produce better image denoising effect in comparison with the global variable using the steepest descent to automatically select the high-fidelity parameters,and the peak signal-to-noise ratio(PSNR)of the proposed method is improved by 0.2～0.5dB under different Gauss noise backgrounds.

Keywords：image denoising;variational theory;wavelet transform;local adaptation

ResearchonAnHigh-fidelityLocalAdaptiveImageDnoisingMethodBasedontheVariationalTheory

QIANWei,LIUQian,CHENLan-ying

(Aircraft Repair Depot,Civil Aviation Flight University of China,Guanghan 618307,China)

TP391.41

A

1008-9233(2017)05-0081-04

2017-08-20

中国民航飞行学院面上基金项目(J2015-09)

钱伟(1986-)，男，四川峨边人，工程师，主要从事检测自动化、图像处理研究。