拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题

喻 昕 许治健 陈昭蓉 徐辰华



拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题

喻 昕①许治健*①陈昭蓉①徐辰华②

①(广西大学计算机与电子信息学院 南宁 530004)②(广西大学电气工程学院 南宁 530004)

非凸非光滑优化问题涉及科学与工程应用的诸多领域，是目前国际上的研究热点。该文针对已有基于早期罚函数神经网络解决非光滑优化问题的不足，借鉴Lagrange乘子罚函数的思想提出一种有效解决带等式和不等式约束的非凸非光滑优化问题的递归神经网络模型。由于该网络模型的罚因子是变量，无需计算罚因子的初始值仍能保证神经网络收敛到优化问题的最优解，因此更加便于网络计算。此外，与传统Lagrange方法不同，该网络模型增加了一个等式约束惩罚项，可以提高网络的收敛能力。通过详细的分析证明了该网络模型的轨迹在有限时间内必进入可行域，且最终收敛于关键点集。最后通过数值实验验证了所提出理论的有效性。

拉格朗日神经网络；收敛；非凸非光滑优化

1 引言

作为解决优化问题的并行计算模型，递归神经网络在过去的几十年里受到了极大的关注，不少神经网络模型被提出。然而这些网络都是为解决光滑优化问题而设计的，它们却无法解决非光滑优化问题。为此，Forti等人[4]提出了通用非线性规划神经网络模型(G-NPC)，用于解决不等式限制的非光滑优化问题。G-NPC是利用Clark次梯度和惩罚项构造的微分包含梯度系统，其动态行为和最优化能力适用于解决凸的和非凸的问题。Bian等人在文献[5]和文献[6]分别提出了利用Clark次梯度神经网络来解决非光滑凸和非光滑非凸最优化问题，通过使用Clark次梯度和惩罚项建立微分包含递归神经网络模型。在此模型下给定一个足够大的罚因子参数，神经元状态轨迹将收敛到平衡点集。此外，Liu等人[7]利用投影方法提出了解决线性等式和R上闭凸子集共同约束的非光滑非凸优化问题的递归神经网络模型。Bian等人[8]利用光滑逼近技术构造光滑神经网络模型解决非光滑非凸的优化问题，在此模型下神经网络的平衡点就是原始问题的最优解。Qin等人[9]提出了一种单层神经网络模型以解决目标函数为伪凸非光滑的优化问题。

目前提出的解决非光滑优化问题的递归神经网络模型大多基于早期罚函数的思想，需要罚因子足够大才能保证网络收敛到优化问题的最优解，因此必须在网络执行计算前计算出罚因子。而这个参数在某些目标函数下是难以计算的，这为网络执行计算带来困难。为此本文拟借鉴Lagarange乘子罚函数的思想提出一种解决非光滑非凸优化问题的递归神经网络模型，该网络模型的罚因子是变量，且无需事先计算罚因子的初始值仍能保证神经网络收敛到优化问题的最优解。此外，与传统Lagrange方法不同，该网络模型增加了一个等式约束惩罚项，可以提高网络的收敛能力。

本论文组织结构如下：第2节，介绍了本文需要解决的优化问题；第3节，介绍了增广拉格朗日神经网络模型；第4节，对该神经网络模型进行相关的理论分析；第5节，给出两个仿真实例验证理论的正确性和有效性。

2 优化问题

本文考虑如下的优化问题：

3 神经网络模型

基于增广拉格朗日函数，我们提出以下神经网络模型以解决优化问题：

上述神经网络模型中参数的作用：(1)凸化目标函数，当参数足够大时，可以使优化问题满足局部凸性；(2)加快网络轨迹的收敛速度。

式(2)给出了神经网络的状态方程，即网络模型的学习方法，这里给出该模型对应的硬件实现及其工作过程(见图1)。当对此硬件电路输入初始电压后，电流会在电路中震荡最终趋于稳定，若电路设计合理，那么电压的稳定值则是原始问题的最优解。

4 主要定理及证明

引理1[6]，当时，有，其中。

图1 神经网络模型的硬件实现

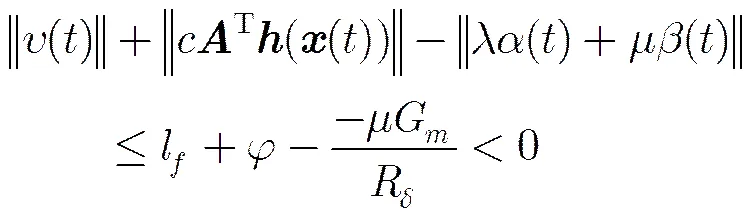
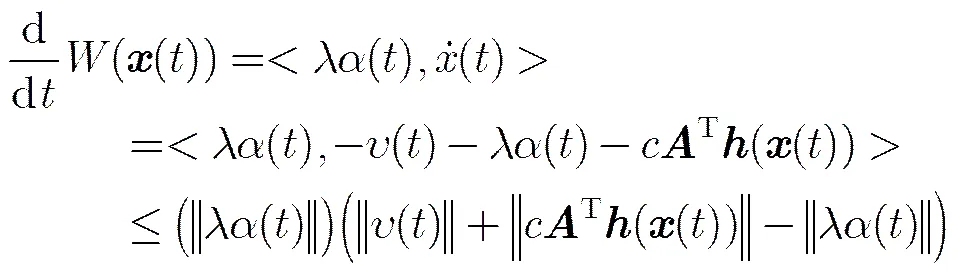
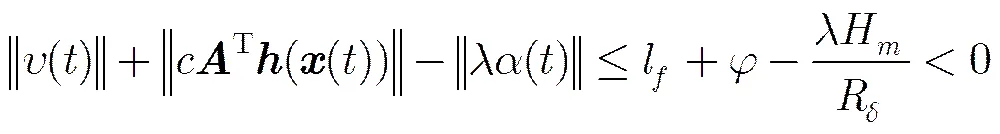
证毕

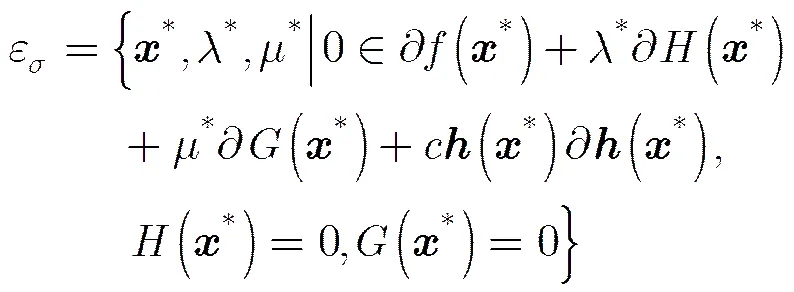
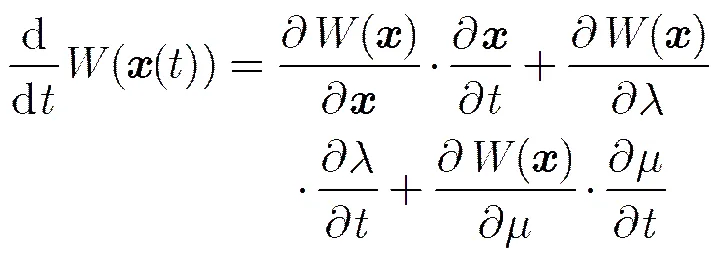
(10)

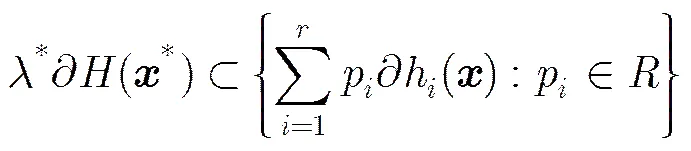
同理，当

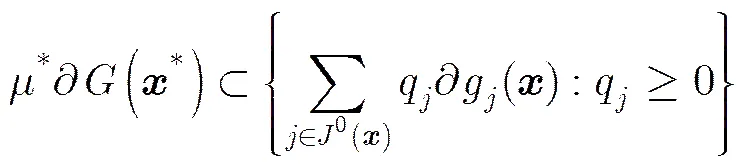
证毕

5 数值仿真及结果分析

仿真实验在MatlabR2012平台下进行，实验包括两个实例：

例1 目标函数为非凸非光滑，限制条件为光滑凸函数

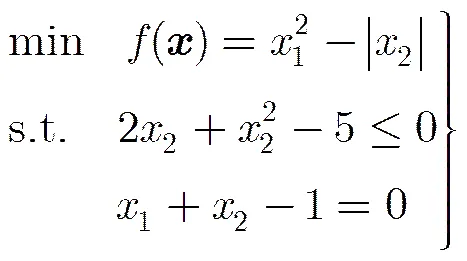
例2 目标函数为非光滑非凸，限制条件包含非光滑凸约束函数

此外，为了比较本文所提出的增广拉格朗日网络模型和传统拉格朗日网络模型，设定初始点，参数分别取，其他参数不变。事实上当增广拉格朗日网络模型就退化为传统拉格朗日网络模型。状态向量的轨迹如图6和图7所示。从图中可以发现，网络随着参数的增加，收敛速度也相应增加，而当时，即在传统拉格朗日网络模型下，网络状态甚至不收敛。

6 结束语

本文旨在解决工程应用中经常出现的含有约束的非光滑非凸优化问题，提出了一种基于拉格朗日思想的神经网络模型，通过增加惩罚约束项以凸化目标函数来求解优化问题，分析了神经网络的收敛轨迹在有限时间内进入可行域，并且最终收敛于平衡点集，同时给出了平衡点集与关键点集的关系。最后实例验证了所提出的增广拉格朗日神经网络求解带等式及不等式约束非光滑非凸优化问题的有效性，同时通过与传统拉格朗日网络模型解决相同问题进行比较，表明其在收敛性方面更优。

图2 例1中的轨迹

图4 例2中的轨迹

图6 取不同值的轨迹

[1] MIAO Peng, SHEN Yanjun, LI Yujiao,. Finite-time recurrent neural networks for solving nonlinear optimization problems and their application[J]., 2016, 177(7): 120-129.doi: 10.1016/j.neucom.2015.11.014.

[2] MESTARI M, BENZIRAR M, SABER N,. Solving nonlinear equality constrained multiobjective optimization problems using neural networks[J]., 2015, 26(10): 19-35. doi: 10.1109/TNNLS.2015.2388511.

[3] HOSSEINI A. A non-penalty recurrent neural network for solving a class of constrained optimization problems[J]., 2016, 73(1): 10-25. doi: 10.1016/j.neunet. 2015.09.013.

[4] FORTI M, NISTRI P, and QUINCAMPOIX M. Generalized neural network for nonsmooth nonlinear programming problems[J]., 2004, 51(9): 1741-1754. doi: 10.1109/TCSI. 2004.834493.

[5] XUE Xiaoping and BIAN Wei. Subgradient-based neural networks for nonsmooth convex optimization problems[J]., 2008, 55(8): 2378-2391. doi: 10.1109/TCSI.2008.920131.

[6] BIAN Wei and XUE Xiaoping. Subgradient-based neural networks for nonsmooth nonconvex optimization problems[J]., 2009, 20(6): 1024-1038. doi: 10.1109/TNN.2009.2016340.

[7] LIU Qingshan and WANG Jun. A one-layer projection neural network for nonsmooth optimization subject to linear equalities and bound constraints[J]., 2013, 24(5): 812-824. doi: 10.1109/TNNLS.2013.2244908.

[8] BIAN Wei and CHEN Xiaojun. Smoothing neural network for constrained non-Lipschitz optimization with applications [J]., 2012, 23(3): 399-411. doi: 10.1109/TNNLS.2011. 2181867.

[9] QIN Sitian, BIAN Wei, and XUE Xiaoping. A new one-layer recurrent neural network for nonsmooth pseudoconvex optimization[J]., 2013, 120(22): 655-662. doi: 10.1016/j.neucom.2013.01.025.

Lagrange Neural Network for Nonsmooth Nonconvex Optimization Problems with Equality and Inequality Constrains

YU Xin①XU Zhijian①CHEN Zhaorong①XU Chenhua②

①(,,,530004,)②(,,530004,)

Nonconvex nonsmooth optimization problems are related to many fields of science and engineering applications, which are research hotspots. For the lack of neural network based on early penalty function for nonsmooth optimization problems, a recurrent neural network model is proposed using Lagrange multiplier penalty function to solve the nonconvex nonsmooth optimization problems with equality and inequality constrains. Since the penalty factor in this network model is variable, without calculating initial penalty factor value, the network can still guarantee convergence to the optimal solution, which is more convenient for network computing. Compared with the traditional Lagrange method, the network model adds an equality constraint penalty term, which can improve the convergence ability of the network. Through the detailed analysis, it is proved that the trajectory of the network model can reach the feasible region in finite time and finally converge to the critical point set. In the end, numerical experiments are given to verify the effectiveness of the theoretic results.

Lagrange neural network; Convergence; Nonsmooth nonconvex optimization

TP183

A

1009-5896(2017)08-1950-06

10.11999/JEIT161049

2016-10-12；

改回日期：2017-04-18；

2017-05-18

许治健 zhongxiawuyu@126.com

国家自然科学基金(61462006, 51407037)，广西自然科学基金(2014GXNSFAA118391)

The National Natural Science Foundation of China (61462006, 51407037), The Natural Science Foundation of Guangxi Province (2014GXNSFAA118391)

喻 昕： 男，1973年生，教授，博士，博士生导师，主要研究方向为人工智能、人工神经网络、优化计算.

许治健： 男，1990年生，硕士生，研究方向为人工神经网络、优化计算.

陈昭蓉： 女，1991年生，硕士生，研究方向为人工神经网络、优化计算.

徐辰华： 男，1976年生，副教授，博士，主要研究方向为过程控制、人工神经网络.