基于贡献函数的重叠社区划分算法

刘功申 孟 魁 郭弘毅 苏 波 李建华



基于贡献函数的重叠社区划分算法

刘功申 孟 魁*郭弘毅 苏 波 李建华

(上海交通大学电子信息与电气工程学院 上海 200240)

现实世界中的网络结构呈现出重叠社区的特征。在研究经典的标签算法的基础上，该文提出基于贡献函数的重叠社区发现算法。算法将每个节点用三元组(阈值、标签、从属系数)集合来表示。节点的阈值是每次迭代过程中标签淘汰的依据，该值由多元线性方程自动计算而来。从属系数用于衡量当前节点与标签所标识社区的相关度，从属系数的值越大说明该节点与标签所标识社区的关联性越强。在每一次迭代的过程中，算法依据贡献函数计算每个节点的从属系数，并生成新的三元组集合。然后依据标签决策规则淘汰标签，进行从属系数规范化。通过对真实的复杂网络和LFR(Lancichinetti Fortunato Radicchi)自动生成的网络进行测试可知，该算法的社区划分准确率高，而且划分结果稳定。

复杂网络；社区发现；重叠社区

1 引言

经典的社区发现算法假设某个节点仅仅属于一个特定社区，这种假设显然和现实不完全相符。在现实世界的复杂网络系统中，存在一些节点同时属于不同的社区，这便是所谓的重叠社区结构[1]。针对重叠社区的挖掘问题，Palla等人[2]提出了针对重叠社区的派系过滤(Clique Percolation Method, CPM)算法，该算法将社区视作由一些互相连通的完全子图构成的集合。将节点数目为的完全子图定义为-clique，当两个-clique之间拥有个公共节点时，则认为这两个-clique是相邻的。自从Palla提出Clique概念以来，许多研究者便不断尝试提出新的基于Clique思想的社区发现算法[3]。

Gregory[4]在GN算法的基础上提出了能发现重叠社区的CONGA (Cluster-Overlap Newman Girvan Algorithm)算法，其主要思想是将边介数较高的节点再分裂成多个副本。对于分裂后的节点，采取经典的社区发现算法进行挖掘社区结构。由于某些节点在算法运行过程中分裂成多个副本，这些副本在后续运行过程中可能被划分到不同的社区，并最终实现一个节点可以同时属于多个社区的目的。

文献[5]采用了非负矩阵分解来发现重叠社区结构，采用非负矩阵分解在重叠社区发现任务上具有很好的准确性和良好的解释性。文献[6]提出了基于非负矩阵分解的图规范化方法，在该方法中使用了能反映节点间相似度的度量方法，实验证明这种方法能提高社区划分的准确度。文献[7]提出了一种基于非负矩阵的半监督社区划分方法，该方法利用了标签的先验知识进行训练，在划分工程中归并标签。

Raghavan等人[8]提出的基于标签传播的社区发现算法(Label Propagation Algorithm, LPA)具有非常好的时间复杂度，这促使Gregory[9]将LPA算法从非重叠社区拓展到了重叠社区，提出了基于标签传播的重叠社区发现算法。Gregory的算法[9]继承了传统标签的优秀的时间复杂度指标，在不同的网络数据上具有较好的测试结果。但是，该算法也具有明显的劣势：(1)继承了传统标签传播算法的缺点—随机性。(2)算法执行时需要事先设置参数，而且的不同取值对算法的结果影响非常大。但如何选择合适的值是个难题。

本文在分析现有算法的基础上，提出基于贡献函数的重叠社区划分标签传播算法(Overlapping- Communities Recognition Algorithm based on Contribution Function, OCRA-CF)。通过引入贡献函数，克服了Gregory算法的随机行为，使算法结果更加稳定。同时能够自动计算各个节点的阈值，避免了Gregory所提算法中值选择问题。此外，OCRA-CF还具有较好的扩展性及并行计算优势。

2 算法设计

OCRA-CF算法的创新改进在于：(1)为每个节点自动计算阈值，该阈值反映了某个节点属于多个社区的可能程度。(2)采用贡献函数计算从属系数。贡献函数反映了邻居节点的贡献情况。(3)采用较稳定的规则进行标签淘汰，最大程度地提高了算法结果的稳定性。

2.1重要函数

在每一次迭代的过程中，算法将决定每一个节点的所有邻接点的标签以及该标签对下一轮的贡献度。算法的核心由4个因素构成：阈值计算、贡献函数、从属系数和选择规则。在本文中，每个节点拥有独特的阈值，并且实现了阈值的自动计算。从属系数都经过规范化处理过程，某个节点的所有从属系数的值相加为1。同样地，贡献函数的取值也经过规范化处理，某个节点的贡献函数的值相加也是1。最后，根据选择规则来决策保留那些标签或者淘汰那些标签。

2.1.1阈值计算 每个节点的阈值和该节点可能所属的社区数相关。事实上，节点的阈值就是该节点所属社区数的倒数。因此，估算社区数是阈值计算的核心任务。但在未执行完该社区划分算法之前，不可能知道每个节点实际属于几个社区，因此，只能采用估算的方法来预测节点可能属于几个社区。本文提出了为每个节点估算所属社区数量的方法，该方法主要包括估算社区度和计算社区数两个步骤。

(1)估算社区度： 所谓社区度就是衡量节点属于多个社区的可能程度。社区度是本文为每个节点计算的一个数值，该值越大说明该节点同时属于多个社区的可能性就越大，反之亦然。

本文把经典网络的标准划分结果作为先验知识，把每个节点的静态特征数据作为后验知识，通过多元线性回归模型拟合出估算社区数的方程。社区数估算函数为

(2)计算社区数： 计算社区数的工作就是根据已知的社区度估算出该节点可能同时属于的社区数量。根据美国认知科学家George的研究，人类短期记忆一般一次只能记住5~9个事物，也就是常说的“7加减2”原则。近年来对社区网络的数据统计分析的结论也证实，现实社会中的自然人或者网络中的虚拟人(即社会网络节点)尽管有较多的圈子存在，但短期内频繁交往的圈子数约为个。基于此，本文把每个节点可能属于社区数的最大值定为9，并按节点的社区度为每个节点赋予区间上的整数值。

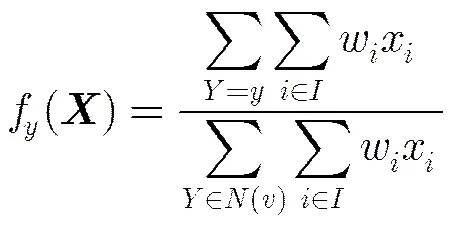
2.1.4标签决策 标签决策是标签选择或淘汰的规则。在算法的每轮迭代中，对于每一个节点，需要按照一定的规则在集合中选择标签或淘汰标签。

2.2参数拟合

2.3 算法流程

算法的整个流程包括4个步骤：计算网络静态特征值、计算阈值、节点赋初值和迭代过程。其中，迭代过程是算法的核心部分，同时也是时间复杂度最高的部分。

(1)计算网络静态特征值： 网络静态特征值是指节点的度(degree)、介数(betweenness)[10]、接近度(closeness)[11]、权威度(authority)[12]等。本文的实验部分使用这几个参数完成了算法。作为对本文的扩展，在实际工程中还可以增加其他参数，或者仅仅使用其中的部分参数。

(2)计算节点阈值： 通过式(1)和式(2)，为每个节点估算出社区数，那么，该节点的阈值()就是社区数的倒数。

(3)节点赋初始值： 迭代开始前为每个节点赋值一个标签，且从属系数为1。每个节点初始状态包含如下两项内容：(只包含一个三元组)和贡献函数表。

(4)迭代过程： 每一轮迭代主要包括3项任务，即从属系数计算、标签决策和终止条件判断。

3 实验与分析

3.1 实验数据

在社区发现算法的研究领域中，有两种方式对算法进行评价。一种是使用现实世界的网络数据集对算法进行测试。由于真实网络结构的复杂性，任何划分都不具有绝对的正确性，因此，需要通过一些社区评价指标作为评价标准。典型的评价指标包括经典算法所提出的函数和Mod模块度[13]等。实验采用了许多具有代表性和研究价值的真实网络数据集。其中包括著名的空手道俱乐部数据集(Karate_Club，简称Karate)、海豚网络数据集(Dolphin_Social，简称Dolphin)、美国大学生职业足球联盟数据集(American_Football，简称Football)、SNS数据集(Social_Community，简称S_C)、豆瓣数据集(Douban)、PGP数据集(PGP)、安然邮件系统数据集(Eron_mail，简称Eron)等。Z_follow是匿名发布者在北邮人(sns.byr.edu.cn)上的所有Follow节点组成的SNS网络。Z_Friends是所有Follow的Follow节点形成的SNS网络。根据数据提供者的说明，Z_Friends网络的模块度是0，也就是说，这个社区不存在小的社区结构。Bupt是整个北邮人SNS网络的所有节点形成的社区。

另一种方式是利用人工构造数据集对算法进行评价。在利用人工构造数据集时，可以通过设定节点数、边数、每个节点的平均度数、重叠度等控制变量来生成结构固定的网络。由于生成的网络结构固定，因此可以有针对性地对算法进行评价。此外，还可以通过改变一到两个构造社区的参数变量，来针对性地测试算法的对不同网络的适应性。Lancichinetti等人[14]提出的LFR基准程序是目前公认的构造人工网络的程序。

3.2式(1)的参数估计

式(1)为典型的多元线性方程，本文采用多元线性回归模型拟合该方程的参数。参数的估计过程主要包括：数据准备和线性回归过程。

(1)数据准备： 国内外科研人员对Karate, Football和Dolphins网络进行了充分研究，给出了公认的划分结果[15]。本文基于这些公认的划分结果，每个节点准备一个标准值，并设计了一个算法来计算该值。该算法主要由以下3个部分组成：

(a)节点连接的社区数： 节点和社区的连接定义为：“如果节点和社区中的任意节点有边相连，则称节点和社区有连接”。根据标准的社区划分，能方便地统计每个节点分别和多少社区有连接(记为)。

(c)指向差异： 指向差异是指某个节点和多个社区连接情况的差异度量。对于节点而言，如果该节点和个社区有连接，且分别有条边连接到社区。当无明显差异时，更倾向于被当作个社区的桥接点，也就是重叠节点。反之，当差异较大时，更倾向于被划分到值较大的那个社区，也就是说不是重叠节点。图1(a)图和图1(c)的节点都倾向于作为社区的节点，而图1(b)的节点更倾向于作为和的桥接点。

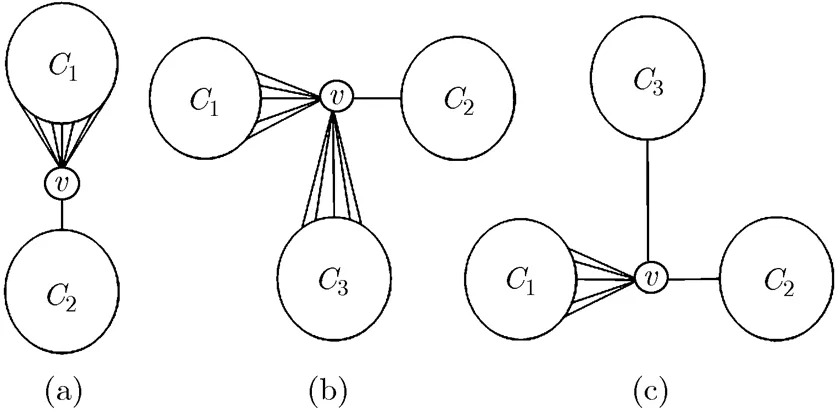
图1 指向差异示意图

因此，指向差异的计算表示为

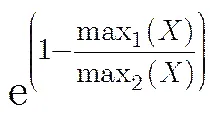
最后，综合上述3部分指标，每个节点的参考值计算公式为

(2)多元线性回归： Karate, Football和Dolphins网络标准划分参见文献[15]。静态值的计算方法同2.3节。由于数据太多，表1仅给出了3个网络的部分参数(分别给出了5个节点的数据)，其他节点的数据略去。根据表1的数据，可以把式(1)的参数确定下来：

(8)

3.3式(4)的参数估计

估算数据时，使用了人工生成网络作为标准,数据集是由Lancichinetti等人[14]开发的LFR基准程序生成的人工数据集。表2中代表节点数；代表网络中节点的平均度数；代表节点的最大度数；代表最小的社区规模，代表最大的社区规模；代表构成这个网络的混合参数。值越大，网络内部的社区结构将越不明显。我们生成了4类人工网络用作参数估计：(1)小网络小社区；(2)小网络大社区；(3)大网络小社区；(4)大网络大社区。

表1标准网络的静态特征值列表(部分)

网络节点度介数接近度权威度式(4)值 Karate1160.4376352810.5689655170.0714127290.066131548 290.0539366880.4852941180.0534272310.283107528 3100.1436568060.5593220340.0637190652.226199031 460.0119092710.4647887320.0424227370.270443437 530.0006313130.3793103450.015260960.520041765 Dolphin160.0190825960.3465909090.0228330682.750868499 280.2133244360.3719512200.0074762740.650780668 340.0090728120.2824074070.0070642181.187597919 430.0023737970.3080808080.0140965461.850075725 5100.2489795920.0052039120.822860534 Football1120.0324899490.4237918220.0100923242.032694610 2120.0176211130.4130434780.0091323661.626829027 3120.0131224970.4071428570.0110170181.539988579 4120.0230700990.4206642070.0100686271.626829027 5110.0106638690.4028268550.0095893771.753784351

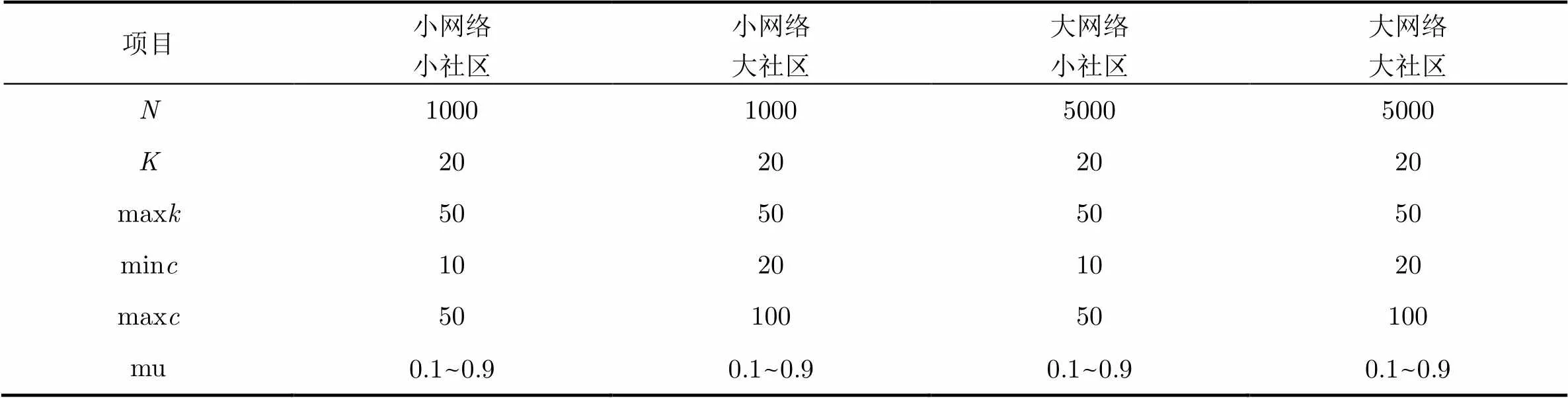
项目小网络小社区小网络大社区大网络小社区大网络大社区 N1000100050005000 K20202020 maxk50505050 minc10201020 maxc5010050100 mu0.1~0.90.1~0.90.1~0.90.1~0.9

图2 独立参数运行情况

3.4真实网络数据集测试

(1)准确性评价： 对于真实网络构成的数据集，采用社区结构参数评价算法结果的好坏。本文主要采用适用于重叠社区发现结果的评价函数Mod进行算法结果的评估。

本文算法(OCRA-CF)是在传统标签算法的基础上改进而来，尽管通过贡献度函数大大降低了算法的不稳定性，但还是保留了一定的标签算法固有的不稳定性与随机性。在针对真实数据集测试的过程中，本文在同一个数据集上先后运行了10次算法。其中Mod值和社区数都是平均值。

经与Karate, Dolphin和football数据集公认的划分结果进行比对，OCRA-CF算法的社区划分结果基本正确，几乎没有节点被错误划分。而对于大规模的网络数据集，从表3中的Mod一列可以看出OCRA-CF算法的运行结果也较为理想。Douban的数据来自于互联网，节点之间的关联度非常低，其社区结构几乎为0。Z_friends的数据也是没有节点之间连接的数据，其社区结构是0，符合数据发布者对数据的特征说明。

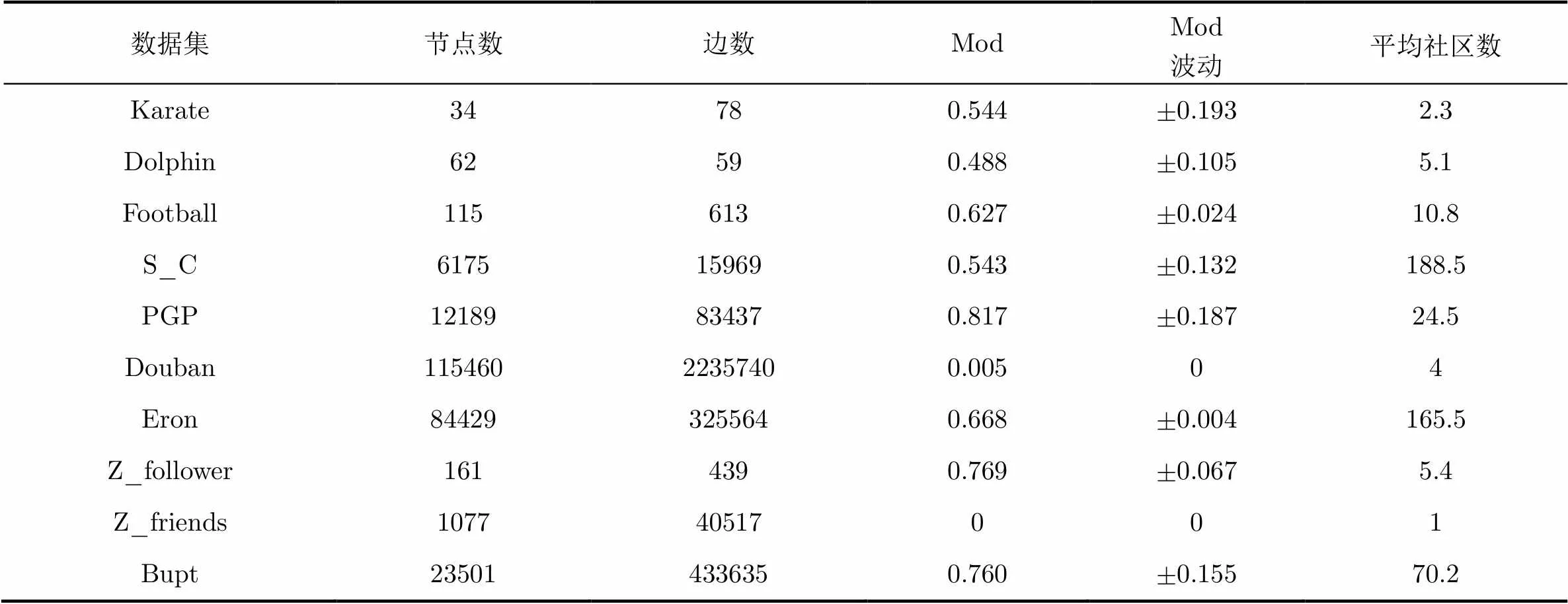
表3 OCRA-CF算法在不同数据集上的运行情况

(2)横向比较： 同样使用上述的测试数据集，我们将OCRA-CF算法与几个经典算法进行了对照测试，结果展示如表4和表5所示，其中，Gregory为文献[9]的算法。

在表4中，OCRA-CF, CPM, Gregory和CFinder算法采用Mod作为评价指标，而GN，Newman采用Q函数作为评价指标，LFM采用EQ评价。表中的OUT表示该算法在24 h内无法完成该数据的计算过程。从表4的数据可以看出，本文提出的OCRA-CF算法在各个数据集上表现都非常好。

在表5中，主要进行运行速度的比较，时间参数为s，从表中的结果可以看出，本文提出的OCRA- CF算法在各种数据集上的时间都较为理想。LFM算法在部分数据集上也表现出了异常优越的效果，但也有些数据的效果非常差，非常不稳定。

总之，OCRA-CF的优势主要有两点：(1)时间复杂度低。经典算法对于大型的数据集，都无法在实验允许的时间内(这里设为24 h)得到社区发现结果。(2)社区划分的模块度适中。在各种数据集上都能获得较好的模块度评价指标。

3.5人工数据集测试

用LFR基准程序所产生的人工网络拥有可控制的社区结构的，因此可以用来对算法的划分准确度进行测试。NMI是评价标准的社区结构和算法输出的划分结构之间的相似度的定量指标。由于考虑到构造的数据集要有相当的规模才能具有测试的代表性，而GN或者CPM算法处理几千节点的数据集时要耗费很长时间，因此本文采用算法复杂度相对较低的LFM算法与CFinder算法作为比较对象。

在对比实验中，使用表2所列的参数生成了4组人工网络。在结果的展示中，OCRA-CF算法、CFinder和LFM算法都取10次重复实验的最佳结果进行比较。算法运行结果所得的NMI如图3所示。各个图中的纵坐标是NMI值，横坐标是的值。4个图的网络属性分别为：(a)小网络/小社区；(b)小网络/大社区；(c)大网络/小社区；(d)大网络/大社区。

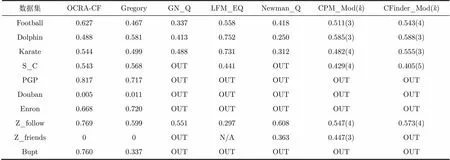
表4 不同算法划分结果的模块度比较

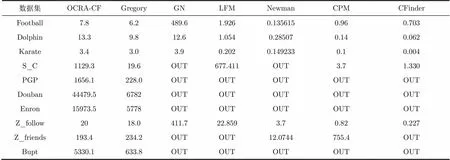
表5不同算法的速度比较(s)

图3 针对人工数据集的准确度比较

4 结论

在现实的社会网络中，社区结构重叠是普遍存在的现象，因此，面向重叠社区的自动发现算法具有重要的研究意义和使用价值。本文提出的基于贡献函数的重叠社区发现算法，即OCRA-CF算法，既继承了传统标签算法的速度优势，又能达到较好的划分效果。通过在各种人工构造数据集和真实数据集上的进行测试，可以看出OCRA-CF运行结果较为理想，达到了可用的目标。在实际工作中，本文算法具还有两大优势：(1)由于OCRA-CF是基于经典标签算法的改进，所以，该算法能比较方便地移植到Hadoop或Spark等并行计算平台，以适应社交网络的大数据需求。(2)OCRA-CF算法中使用的贡献函数具有较强的扩展性，可以通过调整采用的网络参数多少以及参数对应的权重获得不同的贡献函数，适应不同的应用场景。

[1] WANG Xiaofeng, LIU Gongshen, PAN Li,. Uncovering fuzzy communities in networks with structural similarity[J]., 2016, 210(1): 26-33.

[2] PALLA G, DERENVI I, FARKAS I,. Uncovering the overlapping community structure of complex networks in nature and society[J]., 2005, 435(7043): 814-818.

[3] LEE C, REID F, McDAID A,. Detecting highly overlapping community structure by greedy clique expansion [C]. ACM International Conference on Paper Presented at SNA-KDD Workshop, Washington DC, USA, 2010. arXiv: 1002.1827.

[4] GREGORY S. An algorithm to find overlapping community structure in networks[J]. LNCS, 2007, 4702(12): 91-102.

[5] SHI Xiaohua. Community detection in social network with pair wisely constrained symmetric non-negative matrix factorization[C]. Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Paris, France, 2015: 541-546.

[6] LIU Xiao, WEI Yiming, WANG Jian,. Community detection enhancement using no-negative matrix factorization with graph regularization[J]., 2016, 30(20): 1650130.

[7] WANG Zhaoxian, WANG Wenjun, XUE Guixiang,. Semi-supervised community detection framework based on non-negative factorization using individual labels[C], The Sixth International Conference on Swarm Intelligence, Beijing, China, 2015, 349-359

[8] RAGHAVAN U N, ALBERT R, and KUMARA S. Near linear time algorithm to detect community structures in large-scale networks[J].&, 2007, 76(3 Pt 2): 036106.

[9] GREGORY S. Finding overlapping communities in networks by label propagation[J]., 2009, 12(10): 2011-2024.

[10] ULRIK B. A faster algorithm for betweenness centrality[J]., 2001, 25(2): 163-177.

[11] EPPSTEIN D and WANG J. Fast approximation of gentrality[J]., 2004, 8(1): 39-45.

[12] KLEINBERG J M. Authoritative sources in a hyperlinked environment[J].(), 1999, 46(5): 604-632.

[13] NICOSIA V, MANGIONI G, CARCHIOLO V,. Extending the definition of modularity to directed graphs with overlapping communities[J].&, 2009, 2009(3): 3166-3168.

[14] LANCICHINETTI A, FORTUNATO S, and RADICCHI F. Benchmark graphs for testing community detection algorithms[J].&, 2008, 78(2): 046110.

[15] CAO Xiaochun, WANG Xiao, JIN Di,. Identifying overlapping communities as well as hubs and outliers via nonnegative matrix factorization[J]., 2013, 03: 2993. doi: 10.1038/srep02993.

Overlapping-communities Recognition Algorithm Based on Contribution Function

LIU Gongshen MENG Kui GUO Hongyi SU Bo LI Jianhua

(,,200240,)

Overlapping is one of the most important characteristics of real-world networks. Based on the classic labeling algorithm, the overlapping-community orientated label propagation algorithm based on contribution function is proposed. In this algorithm, each node is indicated by a set of triples (threshold, label, and coefficient). The threshold value of every node is used as a metric for labels decision, which is calculated automatically by multiple linear regression equation. The dependent coefficient is used to measure the relevance of the current node with the correspondent community which is marked by the label. A greater value of dependent coefficient means a stronger association between the node and the community. During each iteration process, the dependent coefficients are calculated through Contribution Function (CF) of each node, and new triples are produced. Then the labels in terms of decision rules are selected, and the dependent coefficients of the node are normalized. According to the tests with real-world networks and automatic generation of LFR (Lancichinetti Fortunato Radicchi) test network, the algorithm can divide communication with high accuracy and robust result.

Complex networks; Communities detecting; Overlapping communities

TP309

A

1009-5896(2017)08-1964-08

10.11999/JEIT161109

2016-10-18；

改回日期：2017-04-24；

2017-05-26

孟魁 mengkui@sjtu.edu.cn

国家973关键技术研究项目(2013CB329603)，国家自然科学基金(61472248)

The National 973 Key Basic Research Program of China (2013CB329603), The National Natural Science Foundation of China (61472248)

刘功申： 男，1974年生，副教授，研究方向为内容安全、自然语言理解.

孟 魁： 女，1973年生，高级工程师，研究方向为移动安全、数据安全和社会网络.

郭弘毅： 男，1992年生，硕士生，研究方向为推荐系统研究.

苏 波： 男，1971年生，副研究员，研究方向为社会网络分析.

李建华： 男，1965年生，教授、博士生导师，研究方向为电子与通信工程、信息安全.