基于MODPSO算法的FPRM电路多约束极性优化方法
符 强 汪鹏君 童 楠 王铭波 张会红
基于MODPSO算法的FPRM电路多约束极性优化方法
符 强①②汪鹏君*①童 楠②王铭波①张会红①
①(宁波大学电路与系统研究所 宁波 315211)②(宁波大学科学技术学院 宁波 315212)
为求解较大规模FPRM逻辑电路中多约束条件下的极性优化问题,该文提出一种基于多目标离散粒子群优化(Multi-Objective Discrete Particle Swarm Optimization, MODPSO)算法的求解方法。首先针对FPRM电路极性设计需要满足延时短、面积小的多约束要求,构建了多目标决策模型。然后结合极性转换算法和MODPSO算法,对电路进行最优极性搜索,以获取电路延时和面积的Pareto最优解集。最后利用17个MCNC Benchmark电路进行测试,并将MODPSO算法与DPSO算法、NSGA-II算法进行实验对比,结果验证了算法的有效性。
FPRM逻辑电路;延时与面积优化;极性搜索;Pareto;多目标离散粒子群算法
1 引言
电路逻辑函数既可表示为基于AND/OR/NOT运算的Boolean逻辑,也可表示为基于AND/XOR或者XNOR/OR运算的RM(Reed-Muller)逻辑。与Boolean逻辑电路相比,RM逻辑电路具有较好的可测性,并且在实现奇偶校验、算术逻辑、通信等功能时具有结构与性能上的显著优势,因而得到越来越广泛的关注。
固定极性RM(Fixed Polarity RM, FPRM)是一种常用的RM逻辑规范表达式,其展开式中的变量以原变量或反变量的形式出现。对于个输入变量的逻辑函数,有个固定极性,对应种FPRM展开式。在FPRM电路中,不同的极性对应不同的逻辑展开式,相应的电路结构及性能也不相同。因此必须在FPRM极性空间中搜索到最优的电路极性,才能获取最优的电路延时、面积及功耗等性能指标。
FPRM电路的逻辑设计面向多目标的并行优化,需要综合考虑延时、面积及功耗等各方面性能,从而提升电路的整体性能,因此FPRM电路极性优化问题实质上是一个多约束条件下的综合优化问题。目前常见的求解方法中,是通过加权函数法将FPRM电路多目标优化问题转化为单目标问题进行处理,以达到多个性能指标并行优化的目的。如文献[4]采用固定权系数,利用目标加权的方法提出求解FPRM电路延时和面积优化问题的方法。文献[5,6]分别采用固定权重及可变权重研究了FPRM电路面积与功耗的综合优化问题。然而加权函数法存在几个问题:(1)对权重系数敏感,不同的权重设置对结果影响较为明显。(2)权重选择严重依赖先验知识,较难接近真实的需求折中。(3)难于获取全部的Pareto最优解。往往只能获取一个或者少数最优解,弱化了优化结果的决策支持能力。因此需要更为有效的方法来实现FPRM电路逻辑设计中的多目标综合优化要求。
多目标智能算法近些年发展较快,并在求解多目标优化问题中得到有效应用。此类方法避免了权重设置,利用Pareto准则确定当前解的非支配关系,从中选择最优个体,引导其余个体进行目标寻优,并通过迭代优化确定适应多个目标函数的最优解集。其中多目标粒子群算法[12]与其他同类算法相比,具有结构简单,易于实现,收敛速度快,强鲁棒性等优点。
延时与面积均为RM逻辑电路设计过程中的关键因素,对电路综合性能起着重要作用。本文针对FPRM电路极性设计中同时考虑延时与面积约束条件的综合优化问题,提出一种基于Pareto优化准则的多目标离散粒子群算法(MODPSO),算法中的粒子代表决定FPRM电路延时与面积的电路极性。利用列表技术进行极性转换,然后通过MODPSO算法搜索电路的Pareto最优极性解集,实现电路延时与面积优化设计。最后将对较大规模MCNC Benchmark电路进行测试以验证算法有效性。
2 FPRM电路延时与面积优化模型
2.1 极性转换
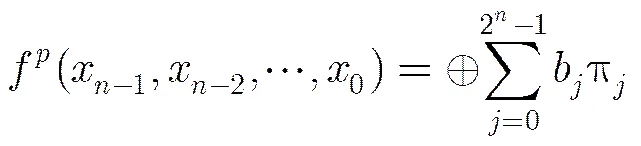
(2)
列表转换技术[13]是一种易于编程实现的快速极性转换算法,适用于含任意变量数的逻辑函数,常被用于FPRM展开式的极性转换。实现从极性转换到极性的列表转换技术算法描述如表1所示。
表1 从极性转换到极性的列表转换技术

BEGIN:初始化,定义集合M, N,并将极性和分别记为 和;将极性下与项序数代表与项,记为 ,并将放入集合M中;FOR TO 0 IF THEN与项生成新与项 ,并存于集合N中;依次将集合N中所有新与项与极性中的与项进行比较,IF 新与项和极性中的与项相同 THEN 在集合M中删除与该新与项相同的对应与项;ELSE 将该新与项添加到集合M中;END
2.2 延时与面积估算模型
在进行电路延时与面积估算之前,先通过代数法化简FPRM表达式,以简化电路结构,利于模型估算优化。代数化简式可描述为
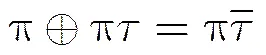

表2 FPRM电路化简算法
在电路逻辑级设计中一般采用单位延时模型估计电路延时。将电路的每个多输入门分解成二输入AND门或XOR门组合,并将二输入门的传输延时大小定义为一个单位时间,则可利用二输入门总数表示电路的面积。而二输入门在关键路径的传输延时之和表示电路延时。二输入门的输出延迟可表示为[15]
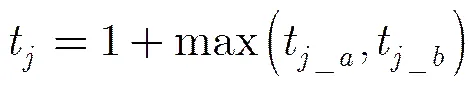
对于化简后的FPRM电路,通过比较多输入门的不同分解方式以找到最短的关键路径延时。设为一个FPRM展开式,为第个向量的子展开式,为逻辑分解后的终端节点向量个数。令原始输入信号的延时为0,则FPRM电路的延迟分解算法可以描述如表3所示。

表3 FPRM电路的延时分解算法
化简及分解后的电路网络表示为(),为二输入门集合。将中的二输入AND门总数记为,二输入XOR门总数记为;并将其中关键路径上的二输入门总数记为。则FPRM电路的延时与面积估算模型可表示为
(5)
(6)
3 多目标离散粒子群优化(MODPSO)
粒子群算法[16]借鉴了鸟群觅食机制,结合粒子自身认知与最优群体提供的社会信息来促进粒子间的信息交流与合作,能迅速定位并捕捉目标。
为利用粒子群算法搜索电路最优极性,对算法进行了离散化,设计了粒子编码方案、粒子更新机制,并构建了实现电路延时与面积综合优化的MODPSO方法,以获取Pareto最优极性解集。
3.1 多目标决策函数
对FPRM电路而言,电路延时长短与面积大小均由电路极性决定。选择合适的电路极性,才能获取延时与面积的综合优化效果。加权函数法为电路延时与面积模型进行权重设定,利用单目标求解方法寻找最优极性。但是面向不同的用户需求,单一的权重设置较难满足电路设计的多样性要求。同时,面积与延时不一定表现出相同的变化趋势:面积最小的极性下电路的延时有可能较长,而延时最短的极性下电路的面积可能较大。因此选用Pareto优化准则作为粒子群体的进化依据,得出多目标决策函数为
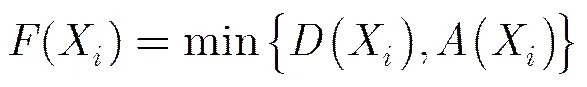
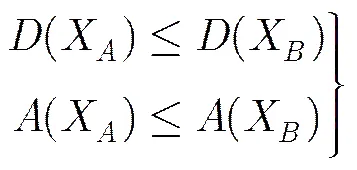
3.2 粒子编码与更新
在求解FPRM电路延时和面积优化问题时,MODPSO中的搜索空间维度对应于 FPRM电路的变量数。粒子位置对应于电路的极性,最优粒子位置则表示FPRM电路优化搜索中的最优极性。
假设粒子种群中的粒子总数为Population,搜索空间为维,随机初始化每一个粒子的位置和速度。记第个粒子的位置为,;其飞行速度为。个体最优位置为;粒子种群最优位置为。由于在离散空间进行最优电路极性搜索,因此需要将算法进行离散化处理。可得粒子速度与位置更新式为
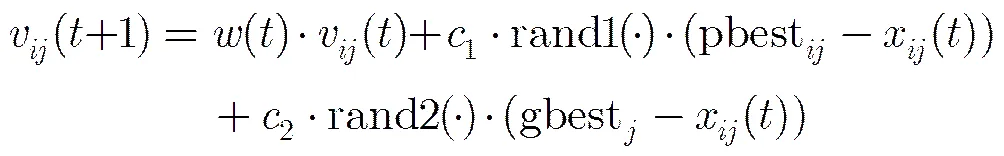
(10)
设置外部存储的最优档案库以保存当前进化代数中得到的Pareto 最优解,并在下一代进化时从中选择带领粒子种群寻优。为保证粒子的多样性要求,最优档案库的粒子按照拥挤程度排序,并利用轮盘赌方式进行全局最优粒子选择。
预先设定最优档案库规模大小,当其中数量较少时,可将新求得的最优粒子直接放入最优档案库中;而当最优档案库中的粒子个数达到或超出预定规模要求时,则需要分析新最优粒子与最优档案库中原有粒子的支配关系,留下其中更优的部分。
为保证粒子的可控性,对粒子进行速度约束,如式(11)所示。

3.3 Pareto最优极性解集搜索
综合以上对FPRM延时与面积估算模型、列表转换技术,以及MODPSO算法设计的分析,提出面向FPRM电路延时与面积综合优化问题的Pareto最优极性解集搜索方案如表4所示。
4 实验与分析
本文实验均在Windows XP操作系统下,通过VC6.0编译。程序的硬件环境为Inter Pentium CPU G645(2.9 GHz) 1.82 GB RAM。测试电路随机取用17个PLA格式的MCNC Benchmark电路。
首先将MODPSO算法与利用加权函数法的DPSO算法[4]进行了实验对比,两种算法各运行20次。参数设置为:粒子总数Population=40,迭代进化次数Iteration=120。加速因子==2;惯性权重=0.4,=0.9;=4, DPSO算法中的优化权重值为0.5。
表5给出了两种算法各自运行Benchmark电路获取的电路延时与面积。其中,“名称”为测试电路的名称,“最好”、“最差”分别为MODPSO算法和DPSO算法20次运行所得最好值与最差值,“Del_A”和“Del_D”分别为MODPSO算法和DPSO算法20次运行结果的面积方差与延时方差。

表4 FPRM电路延时与面积综合优化问题的Pareto最优极性解集搜索方案
从表5数据可以看出,当电路中的延时与面积具有相同变化趋势,Pareto最优解集中只有唯一解时,DPSO有机会求取满足最优延时与面积的极性结构,但由于文献中的DPSO算法将延时与面积权重均固定为0.5,并不适合每个具有不同特征的电路,在电路 in5, s444, x9dn测试中所求得最优解精度不如MODPSO算法,并在大部分电路测试中表现出较大波动性,最差解质量明显劣于MODPSO算法。MODPSO算法不需要进行权重设置,且针对各种类型的电路均能获得较好结果。同时其20次运行结果的方差小,具有较强的鲁棒性。尤其对于电路a12,由于该电路延时与面积具有不同的变化趋势,Pareto最优解集中的非劣解不唯一,DPSO算法无法求得全部Pareto最优解,而MODPSO算法能够稳健获得Pareto最优解集。
为进一步验证MODPSO算法在求解FPRM电路延时和面积问题的有效性和可靠性,将算法与NSGA-II算法[10]进行实验比对。针对每个测试电路,MODPSO算法与NSGA-II算法分别实验20次,结果如表6所示。其中“次数”表示在20次测试中,获得最优解的总次数;“时间(s)”为20次测试所花费的总时间。

表5 MODPSO与DPSO算法最优极性对应的延时与面积
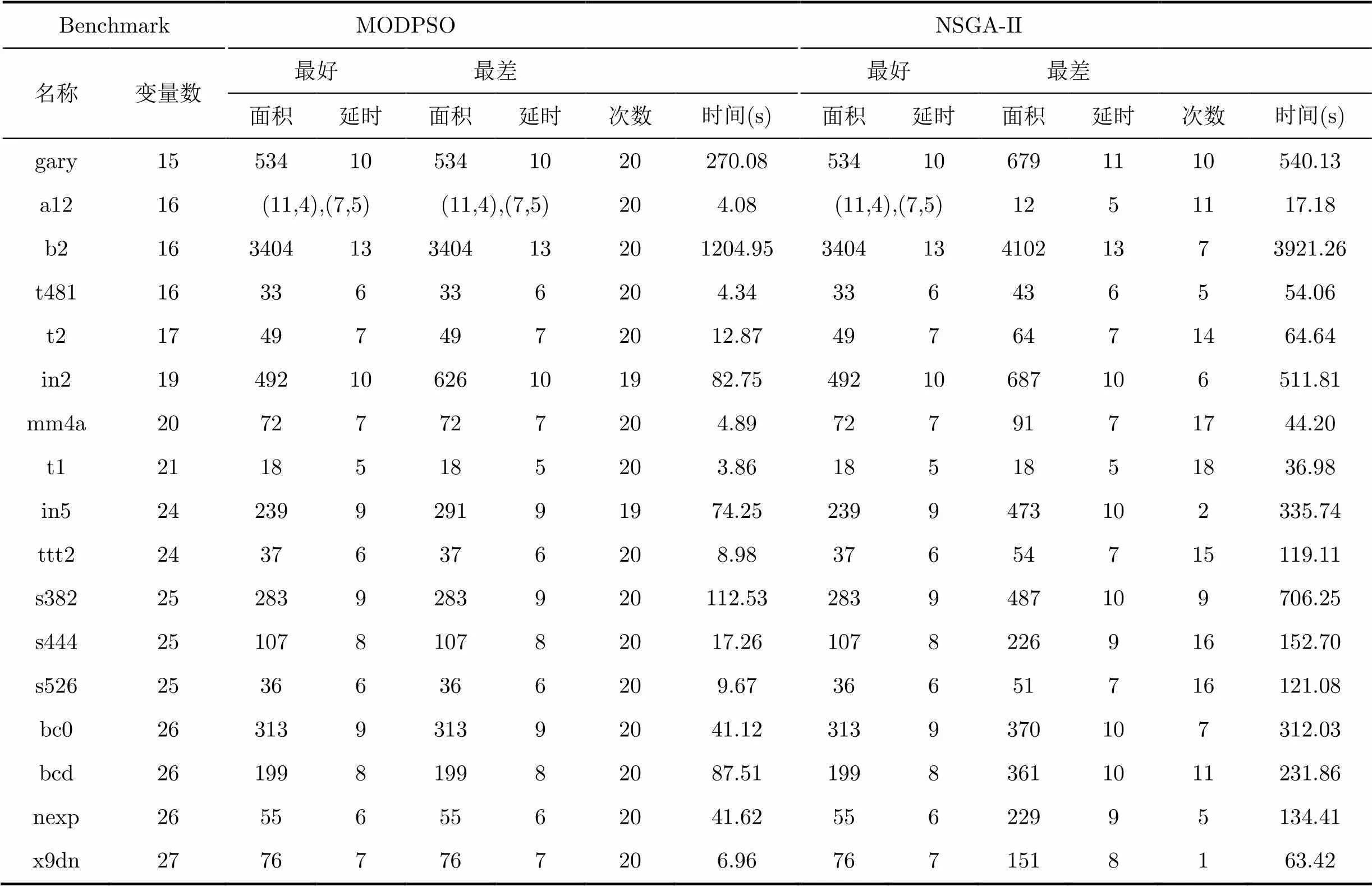
表6 MODPSO与NSGA-II算法最优极性对应的延时与面积
从表6中可以看出,在每个测试电路的实验结果中,NSGA-II算法均有机会获取最优解,但在20次实验结果中表现出较大差异性:17个电路测试中求得最优解的平均概率仅为49.68%,且对于a12电路,有9次测试未能获得Pareto最优解集;而MODPSO算法相比NSGA-II算法具有明显更优的求解性能,在15个电路测试中均能20次全部获取最优解,且在17个电路测试中求得最优解的平均概率达到99.4%,表现出良好的算法鲁棒能力。
在时间花费上,NSGA-II算法在全部电路测试上花费的总时间为7366.86 s;而MODPSO算法花费的总时间为1987.76 s,仅为前者的26.98%。
就整体测试结果而言,MODPSO算法相比NSGA-II算法,17个测试电路的延时优化率平均值为13.22%,面积优化率平均值为2.51%。延时优化率及面积优化率可描述为
延时优化率=(OD1-OD2)/OD2 (12)
面积优化率=(OA1-OA2)/OA2 (13)
其中OD1, OD2分别为NSGA-II算法、MODPSO算法20次优化结果获取的延时平均值, OA1, OA2分别为NSGA-II算法、MODPSO算法20次优化结果获取的面积平均值。
将17个测试电路的20次优化结果之和作为最终测试结果,分析两种算法的面积与延时迭代进化过程,如图1,图2所示。
从图1,图2中可以看出, NSGA-II算法进化速度慢,而且较早陷入早熟收敛;而MODPSO算法在进化早期就表现更优的搜索效率,具有更强的全局搜索能力。
5 结束语
针对FPRM电路极性设计中的多目标优化问题,本文提出了一种基于MODPSO算法的极性搜索方法,利用Pareto优化准则进行多目标条件下的粒子优劣性评价,以获取延时和面积综合优化的电路最优极性解集。对17个PLA格式的MCNC Benchmark电路进行了测试,实验结果表明,MODPSO算法避免了加权函数法对权重设置的主观性,能获取更加准确、完整的Pareto最优解,提高了电路辅助设计能力。而与加权函数法及NSGA- II算法相比,MODPSO算法在求解精度、速度及鲁棒性等方面均具有更好的优化效率。
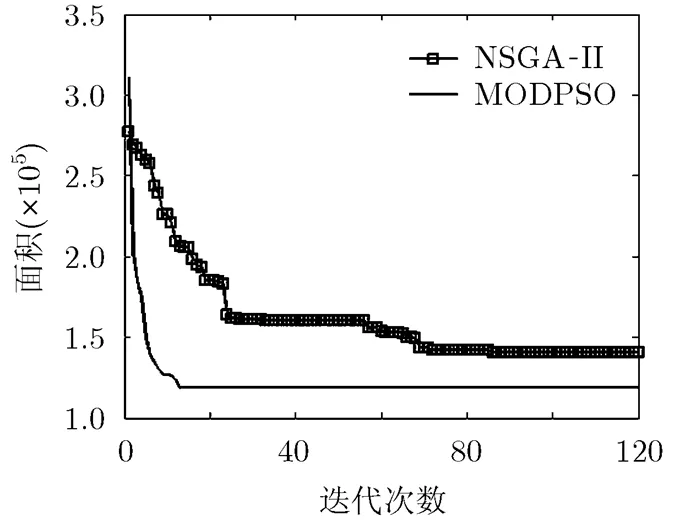
图1 电路数据集面积进化曲线

图2 电路数据集延时进化曲线
[1] MONREIRO C, TAKAHASHI Y, and SEKINE T. Low- power secure S-box circuit using charge-sharing symmetric adiabatic logic for advanced encryption standard hardware design[J].,&, 2015, 9(5): 362-369.
[2] 王伦耀, 夏银水, 陈偕雄. 逻辑函数的双逻辑综合与优化[J]. 计算机辅助设计与图形学学报, 2012, 24(7): 961-967.
WANG Lunyao, XIA Yinshui, and CHEN Xiexiong. Logic synthesis and optimization based on dual logic[J].-&, 2012, 24(7): 961-967.
[3] 卜登立, 江建慧. 基于混合多值离散粒子群优化的混合极性 Reed-Muller 最小化算法[J]. 电子与信息学报, 2013, 35(2): 361-367.doi: 10.3724/SP.J.1146.2012.00790.
BU Dengli and JIANG Jianhui. Hybrid multi-valued discrete particle Swarm optimization algorithm for mixed-polarity Reed-Muller minimization[J].&, 2013, 35(2): 361-367. doi: 10.3724/ SP.J.1146.2012.00790.
[4] 王振海, 汪鹏君, 俞海珍, 等. 基于PSO算法的FPRM电路延时和面积优化[J]. 电路与系统学报, 2012, 17(5): 75-80.
WANG Zhenhai, WANG Pengjun, YU Haizhen,. Delay and area optimization for FPRM circuits based on PSO algorithm[J]., 2012, 17(5): 75-80.
[5] WANG Pengjun, LI Kangping, and ZHANG Huihong. PMGA and its application in area and power optimization for ternary FPRM circuit[J]., 2016, 37(1): 015007.
[6] DAS A and PRADHAN S N. Thermal aware FPRM based AND-XOR network synthesis of logic circuits[C]. IEEE 2nd International Conference on Recent Trends in Information System(ReTIS). IEEE, Kolkata, India, 2015: 497-502. doi: 10.1109/ReTIS.2015.7232930.
[7] 姜兴龙, 梁广, 刘会杰, 等. 一种新型的低轨存储转发通信星座设计方法[J]. 电子与信息学报, 2014, 36(3): 676-682.doi: 10.3724/SP.J.1146.2013.00551.
JIANG Xinglong, LIANG Guang, LIU Huijie,. A new design method of store and forward LEO communication satellite constellation[J].&, 2014, 36(3): 676-682. doi: 10.3724/ SP.J.1146.2013.00551.
[8] ESFAHANI I J, YOO C K, KALOGIROU SOTERIS A,. An optimization algorithm-based pinch analysis and GA for an off-grid batteryless photovoltaic-powered reverse osmosis desalination system[J]., 2016, 91: 233-248.
[9] SRIVASTAV A and AGRAWAL S. Multi-objective optimization of hybrid backorder inventory model[J]., 2016, 51: 76-84.
[10] MARTINEZ-VARGAS A, DOMINGUEZ-GUERRERO J, ANDRADE Á G,. Application of NSGA-II algorithm to the spectrum assignment problem in spectrum sharing networks[J]., 2016, 39: 188-198.
[11] YUAN Y, XU H, WANG B,. A new dominance relation-based evolutionary algorithm for many-objective optimization[J]., 2016, 20(1): 16-37.
[12] HOAI BACH NGUYEN, XUE Bing, LIU Lü,. New mechanism for archive maintenance in PSO-based multi- objective feature selection[J]., 2016: 1-20. doi: 10.1007/s00500-016-2128-8.
[13] JASSANI B A Al, URQUHART N, and ALMAINI A E A. Manipulation and optimization techniques for Boolean logic[J]., 2010, 4(3): 227-239.
[14] 汪鹏君, 王振海, 陈耀武, 等. 固定极性Reed-Muller电路最优延时极性搜索[J]. 浙江大学学报: 工学版, 2013, 47(2): 361-366.doi: 10.3785/j.issn.1008-973X.2013.02.026.
WANG Pengjun, WANG Zhenhai, CHEN Yaowu,. Searching the best polarity for fixed polarity Reed-Muller circuits based on delay model[J].(), 2013, 47(2): 361-366. doi: 10.3785/j.issn.1008-973X. 2013.02.026.
[15] CORTADELLA J. Timing-driven logic bi-decomposition[J].-, 2003, 22(6): 675-685.
[16] AMINBAKHSH S and SONMEZ R. Discrete particle swarm optimization method for the large-scale discrete time–cost trade-off problem[J]., 2016, 51: 177-185.
Multi-constrained Polarity Optimization of Large-scale FPRM Circuits Based on Multi-objective Discrete Particle Swarm Optimization
FU Qiang①②WANG Pengjun①TONG Nan②WANG Mingbo①ZHANG Huihong①
①(,,315211,)②(,,315212,)
For multi-constrained polarity optimization of large-scale FPRM circuits, a Multi-Objective Discrete Particle Swarm Optimization (MODPSO) algorithm is proposed. Firstly, the multi-objective decision model is established according to the delay-area trade-off of large-scale FPRM circuits. Secondly, combined with tabular technique and MODPSO, the best polarities of delay and area are searched for large-scale FPRM circuits, to obtain the Pareto optimal set for delay and area. Finally, the algorithm MODPSO is compared with the algorithm DPSO and NSGA-II on MCNC Benchmarks with PLA format, and the results verify the effectiveness of the MODPSO.
FPRM circuits; Delay-area trade-off; Polarity search; Pareto; Multi-Objective Discrete Particle Swarm Optimization (MODPSO)
TN79+1; TP391.72
A
1009-5896(2017)03-0717-07
10.11999/JEIT160458
2016-05-05;改回日期:2016-10-18;
2016-12-20
汪鹏君 wangpengjun@nbu.edu.cn
国家自然科学基金(61306041, 61234002),“十二五”浙江省高校重点学科—计算机应用技术,浙江省教育厅科研项目(Y201326770),宁波市自然科学基金(2014A610069,2015A610107)
The National Natural Science Foundation of China (61306041, 61234002), The Twelfth Five-Year Plan of Zhejiang Province Key Discipline (Computer Application Technology), The Scientific Research Fund of Zhejiang Provincial Education Department (Y201326770), The Ningbo Natural Science Foundation (2014A610069, 2015A610107)
符 强: 男,1975年生,讲师,博士生,研究方向为低功耗集成电路理论及优化设计.
汪鹏君: 男,1966年生,博士,教授,博士生导师,研究方向为多值逻辑和低功耗集成电路理论及优化设计.
童 楠: 女,1981年生,讲师,硕士,研究方向为多目标智能优化方法.
王铭波: 男,1994年生,硕士生,研究方向为低功耗集成电路理论及优化设计.

