PDC钻头井底水力参数理论与数值模拟研究

刘照义，张凌峰，王翠姣



PDC钻头井底水力参数理论与数值模拟研究

刘照义1，张凌峰2，王翠姣2

（1. 东北石油大学，黑龙江大庆 163318； 2. 燕山大学，河北秦皇岛 066000）

为了精确计算模拟钻井过程井底水力参数，以Solidworks制图软件建立了三维模型，利用流体力学软件Fluent的模型对井底PDC钻头进行了三维流场数值模拟，从理论计算和数值模拟对喷嘴流量，冲击力和水功率两方面分析了PDC钻头水力参数，分析结果证明数值模拟能够较为精确地描述井底不同方位影响的水力参数，为优化PDC钻头水力参数与井底流场理论研究提供了重要依据，具有良好的参考价值。

PDC钻头；井底流场；数值模拟；fluent

油气勘探开发难度日益增大，要求勘探开采技术的不断提高以需要满。PDC钻头是钻井过程中实现高效、快速、经济钻进破岩的尖刀队，更是油气现场更广泛应用的技术之一。常规理论计算对井底研究结果粗略，而目前油气井学者运用CFD软件实现了数学模型对计算机模拟图形可视化的过程，从模拟结果图形可以粗略观查分析流线场，速度矢量场以及压力场，但对于某些水力参数未曾精确获得。

计算流体力学软件可以较为精确计算井底流场，笔者运用fluent后处理功能实现计算机图形对数学结果的再次转换，进而数值化地研究清楚PDC钻头在井底的水力参数，对于冷却润滑钻头，清洗岩屑，高效经济勘探开发，提供了重要手段依据。

1 常规钻头水功率理论研究

当前，PDC钻头水功率的研究主要是参考钻井相关教材[1]所研究的已广泛应用的理论公式。其中，多数参数计算多为粗略计算，对于不同结构、不同方位，不能够很好的反映井底参数。在钻进过程只能靠增大泵送量等改善井底环境，那么，就会造成能量的损失与浪费，造成经济的浪费。

喷射式钻头的主要水力结构特点是在钻头上安放具有一定结构特点的喷嘴。钻井液通过喷嘴后，能形成具有一定水力能量的高速射流，以射流冲击的形式作用于井底，从而清除井底岩屑和破碎井底岩石。喷嘴以其不同的结构，相应的射流能量不同。射流的主要作用有冲击压力作用和漫流横推作用两种。

射流水利参数包括：射流水力速度、射流冲击力、射流水功率三种。

钻头喷嘴出口处的射流速度称为射流喷射速度，习惯上称为喷速。其计算式为

其中：

（2）

—通过钻头喷嘴的钻井液流量，L/s；

A—喷嘴出口截面积，cm2;

d—喷嘴直径(=1,2,…,)，cm;

—喷嘴个数。

射流在其作用的面积上的总作用的大小称为射流冲击力。其形式为

式中：j——射流冲击力，kN；

单位时间内射流所具有的做功能量，称为钻头水功率。其表达式为

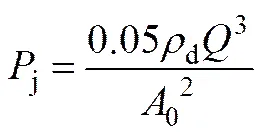
式中:j——射流水功率，kW。

2 数值模拟射流水力参数

要在实际工程中按照钻井液粘度排量的不同而计算各个喷嘴出口的实际水力参数就显得及其困难。而钻头实际水力参数对于高效、快速、安全钻井有着及其重要的意义。受地层岩性或钻井液参数影响，钻头某个喷嘴处流量减少或堵塞，会出现泥包[2]现象，切削齿受冷却润滑作用降低，会产生刀齿高温碳化崩齿现象，井底岩屑清洗不彻底，会出现压实和重复磨削现象[3]。这样就对保质保量、快速安全钻井、水力携岩破岩[4]就产生严重影响。

（1）笔者首先根据现场某简单钻头，利用制图软件Solidworks建立模型，然后带入水力计算软件fluent设置边界条件进行计算，对最终结果进行分析研究，与理论公式结果进行对比分析（图1）。

图1 三维钻头模型

Fig.1 3D bit model

（2）带入Fluent进行计算

将绘制模型带入workbench进行流道设置，绘制网格，最终带入Fluent设置边界条件。以液态水作为流体，即钻井液，选择模型。钻头以及流体的相关参数如表1。

表1 相关参数表

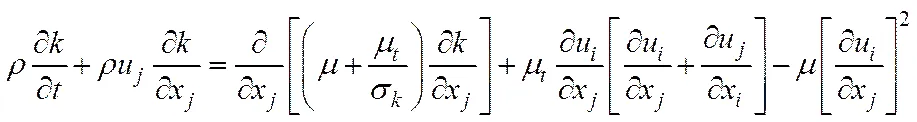
（6）

采用N-S方程[5],湍流动能方程和扩散方将参数设置好带入Fluent得出流场结果如图2-4。

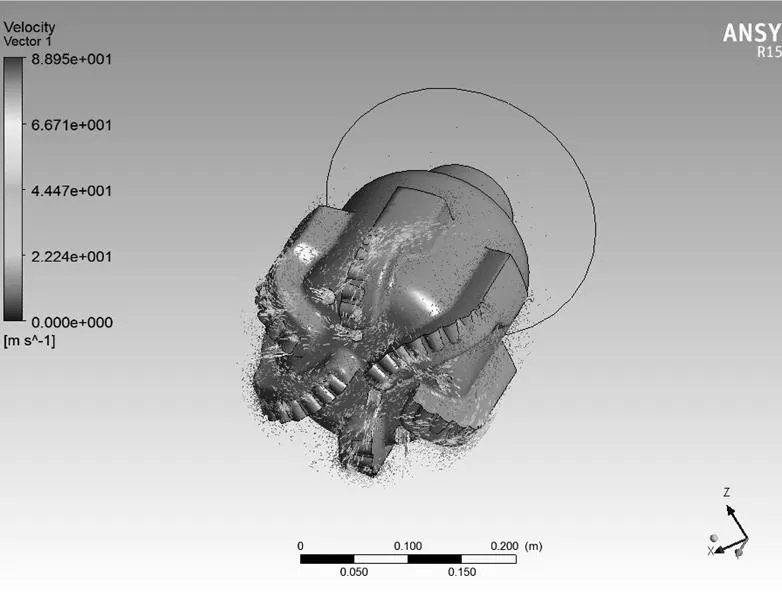
图2 速度矢量图

Fig.2 Velocity vector chart

图3 流线分布图

Fig.3 Streamline distribution diagram

图4 流场速度分布图

由以上计算结果分析可得，钻井液自钻头[6]内部流入井底并反出井底过程中，流速在喷嘴出口位置流速最大，相应的流体冲击井底后，流速环内核速度瞬间为零而压力瞬间增大，可用于[7]冲击破碎岩石，清洗岩屑。

利用CFD-POST后处理功能中的Table功能，将所得结果进行数值显示，结果如表2。

表2 模拟结果参数表

由图2可以看出，对于不同角度，不同方位的喷嘴，在相同工作环境和尺寸条件下，结果各不相同。那么，对于理论公式计算的平均各个喷嘴的水力参数精确度就显得略微欠缺，即难以描述各喷嘴流出的钻井液冷却润滑作用[8]的差异性。

3 理论计算与数值模拟对比分析

3.1 理论公式计算

根据已知参数条件，带入常规理论公式进行计算，得到结果如表3。

表3 理论结果参数表

3.2 射流参数计算研究

将上述数值带入理论公式直接计算和在fluent中建立相应平面，在绘制平面直接求解，得出射流参数如表4。

表4 理论公式与数值模拟结果

通过对比分析两种方式，由表4、图5和图6可以看出，数值模拟计算的喷嘴流量略小于理论公式计算结果；数值模拟计算井底壁面所受最大射流冲击力要小于理论值；相应的数值模拟的射流功率[9]与理论值相差很大。

深层次考虑研究理论与数值模拟[11]结果的差异得出以下结论：对于PDC钻头结构[12]不同，主要是喷嘴方位结构以及角度存在差异，加上各种泵排量工况下，各个喷嘴的数值计算所得流量与理论值有差异且不同结构喷嘴结果不同；在钻井液喷出喷嘴后，受井底扰动耗损、流体粘度[13]、以及喷射距离、流速核的尺寸等诸多因素影响，喷嘴作用在井底的冲击力要比理论值减小；相应的喷嘴的水功率也就大大减小，即理论值乘以修正参数所得结果即为实际值，上述计算的射流水功率为0.588。另外，数值模拟[14]研究本身也有一定微小误差，这也是产生差异的因素之一。

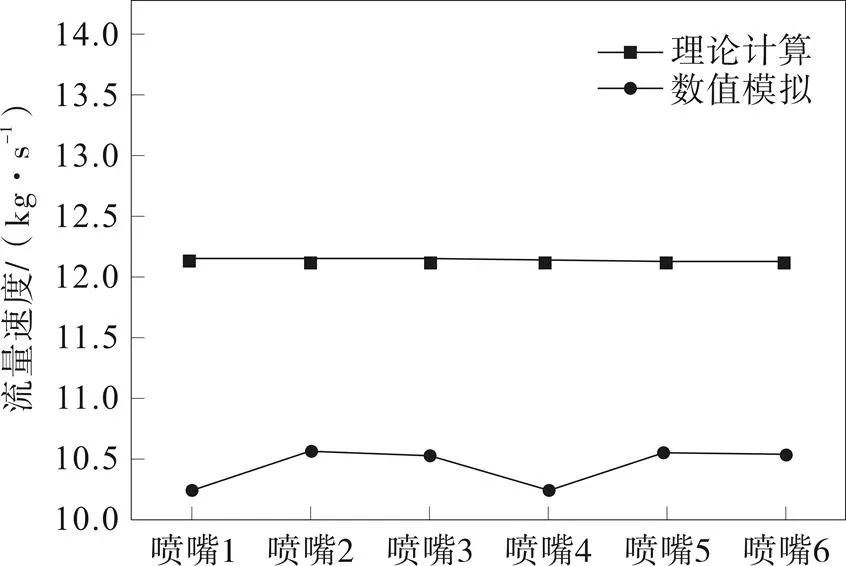
图5 喷嘴流量图

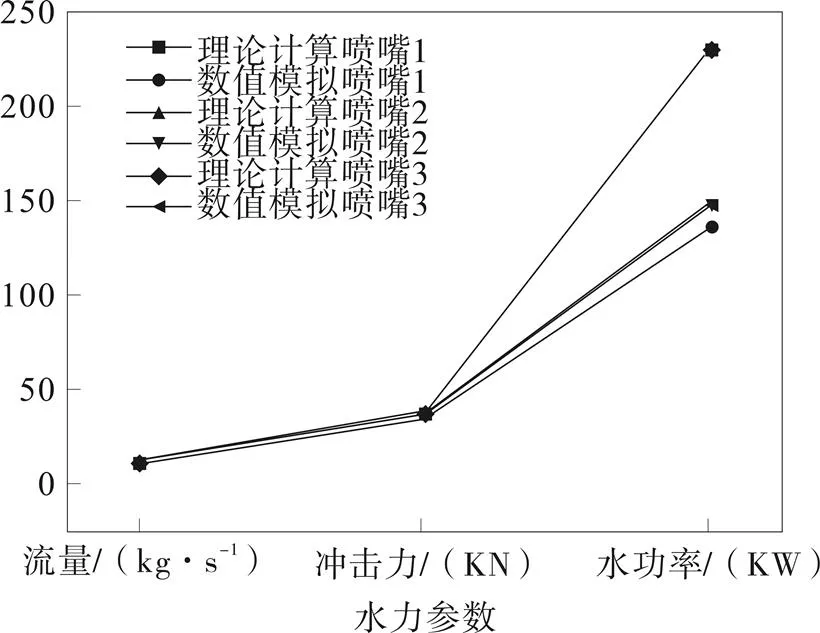
图6 喷嘴1、2、3水力参数对比图

4 工程问题研究应用

根据类似方法，计算流体力学数值模拟在现场已开始研究应用。

4.1 流场模拟案例

学者李根生、陈修平等人运用计算流体力学，研究了井底流场数值模拟，研究了钻头防泥包等问题；于洪石等人运用计算流体力学方法，研究了PDC钻头超高压射流特性与喷嘴设计；祝效华等人根据井底流场速度矢量，研究了清洗岩屑等问题；况雨春等人根据井底流场数值模拟，研究了喷嘴对切削齿的影响等问题；于小龙等人运用中心分区式流场模拟，研究了各刀翼流量配比[15]等问题。

4.2 常规计算水力参数与数值模拟对比

在实际生产与工程问题中，对于常规试验研究方法，试验条件多为高压、高温、高排量，制造与改进模型难度大、成本高、耗时、操作与试验条件等影响，其结果往往存在一定误差，而计算流体数值模拟[16]正好解决了上述问题，并且模拟起来方便，且结果也具有很高的参考价值，是未来被广泛运用于现场或生产制造[17]的热门手段。

5 结论

（1）运用计算流体力学对井底射流水力参数进行数值模拟，可实时反应不同结构、方位角度以及排量下井底的流场情况。结果得出喷嘴角度越接近垂直，流体速度方向改变较小，越利于流体流动，则喷嘴流量速度越大。根据模拟结果对理论公式进行修正，提出该PDC钻头水力射流功率修正参数为0.588。

（2）利用模拟计算得到的水力参数可以快速、便捷地分析解决工程问题，如防泥包、清洗岩屑、减少冲蚀、冷却钻头、优化排量与优化钻头冠部结构等，是日趋受欢迎的井底流场研究手段之一。

（3）利用计算流体力学方法与软件与后处理功能，建立了一种便捷式研究钻头射流水功率的数值模拟思路，更加快速、经济、省时。但计算流体力学本身具有微小误差，对计算结果也会造成细微影响。

［1］陈庭根,管志川.钻井工程理论及技术[M].北京:石油大学出版社,2000.

［2］陈修平,邹德永,李东杰,娄尔标. PDC钻头防泥包性能数值模拟研究[J]. 石油钻探技术,2015,06:108-113.

［3］史怀忠,李根生,王学杰,等. 水力脉冲空化射流欠平衡钻井提高钻速技术[J]. 石油勘探与开发,2010,01:111-115.

［4］马东军,李根生,牛继磊,等. 多孔射流钻头破岩钻孔规律试验研究[J]. 流体机械,2015,03:1-5+16.

［5］况雨春,曾恒,周学军,等. PDC钻头水力结构优化设计研究[J]. 天然气工业,2006,04:60-61+67+155.

［6］祝效华,邓福成,贾彦杰,等. PDC钻头流场数值仿真与水力结构优化[J]. 石油机械,2010,08:1-4+104.

［7］李士斌,张立刚,荆玲,等. 钻井参数优选新方法[J]. 石油钻探技术,2007,04:9-11.

［8］李子丰. 钻柱涡动理论研究的必由之路——钻井液动力润滑学与钻柱动力学相结合[J]. 石油学报,2013,03:607-610.

［9］李垒,金俊卿,陈坤,等. 基于FLUENT软件分析旋风分离器的结构优化[J]. 天然气与石油,2014,03:71-75+13.

［10］况雨春,杨云山,杨迎新,等. PDC钻头井底流场CFD仿真及二次开发[J]. 钻采工艺,2007,01:77-79+148.

［11］谢翠丽,杨爱玲,陈康民. 非对称多喷嘴平底钻头井底三维流场数值模拟[J]. 石油学报,2002,06:77-80+1.

［12］邹德永,梁尔国. 硬地层PDC钻头设计的探讨[J]. 石油机械，2004，09:28-31+84-85.

［13］曹献平,旷曦域,刘英波,等. 泡沫欠平衡钻地热井井筒多相流特性研究[J]. 天然气与石油,2013,04:48-50+9.

［14］任连城,梁政,钟功祥,等. 基于CFD的水力旋流器流场模拟研究[J]. 石油机械,2005,11:22-24+53+5-6.

［15］林铁军,练章华,陈世春,等. 气体钻井中气体携岩对钻杆的冲蚀机理研究[J]. 石油钻采工艺,2010,04:1-4.

［16］付加胜,李根生,史怀忠,等. 水力脉冲空化射流钻井技术适应性分析[J]. 石油钻采工艺,2012,05:10-14.

［17］陈国庆. PDC钻头的发展趋势[J]. 石油机械,2003(S1):103-106.

Theoretical and Numerical Simulation on the Hydraulic Parameters of PDC Bit

1,2,2

（1. Northeast Petroleum University, Heilongjiang Daqing 163318，China;2. Yanshan University, Hebei Qinhuangdao 066000, China）

In order to accurately calculate the hydraulic parameters of wellbore, the three-dimensional model was established by using Solidworks software, and the three-dimensional flow field of PDC bit was simulated by fluid model Fluent.The hydraulic parameters of the PDC bit were analyzed by theoretical calculation and numerical simulation. The results show that the numerical simulation can accurately describe the hydraulic parameters of the PDC bit, which can provide an important basis for optimization of the PDC bit hydraulic parameters and research on bottom hole flow field theory.

PDC bit; Bottom hole flow field; Numerical simulation; Fluent

TE 242

A

1671-0460（2017）06-1152-04

2016-12-03

刘照义（1992-），男，河北省石家庄市人，东北石油大学研究生，研究方向：油气井工程与流体力学。E-mail：846382907@qq.com。