一类非自治密度依赖的时滞捕食者-食饵系统的一致持久性

蒋燕, 杨喜陶



一类非自治密度依赖的时滞捕食者-食饵系统的一致持久性

蒋燕, 杨喜陶

(湖南科技大学数学与计算科学学院, 湖南湘潭, 411201)

研究了一类非自治密度依赖的时滞捕食者-食饵系统的动力学行为。通过利用比较原理来研究它的一致持久性, 得到了该系统一致持久性的充分条件。

捕食者-食饵系统; 一致持久性; 密度依赖; 时滞

捕食与被捕食是自然界中一种非常普遍的生物现象, 捕食-食饵模型是种群动力学模型中一类非常重要的模型, 一直以来受到生态学界和生物数学界的共同关注。李海银等[1]研究了基于比率的非自治的 捕食者-食饵模型解的一致持久性。模型中:代表食饵数量密度;代表捕食者数量密度;和是连续有界函数, 其上下界均为正常数。食饵以内在增长率生长, 在没有捕食情况下接近环境最大容纳量。分别代表捕食者死亡率、捕获率、半饱和率、转换率。许多学者对该模型的持久性[2-4]、周期解的唯一性[5]、平衡点的稳定性[6-7]等性质做了深入而系统的研究。

生物在长期的协同进化过程中逐渐形成了适应环境的生态对策, 时滞现象是物种生态对策的形式之一[8]。例如虎、狼、兔、象等许多哺乳动物具有各自的孕期, 幼子在哺乳期一般没有捕食能力或能力很弱, 需要一段时间的学习后才能成为真正的捕食者。这些时滞因素是构建生态数学模型时应该考虑的参数[9-10]。基于此, 本文将研究非自治密度依赖的时滞捕食者-食饵系统

的一致持久性。

1 一致持久性

定理1 假设

成立, 则方程(1)的解为一致持久。

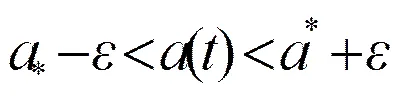
由式(5)类似可证

为完成定理证明, 考虑2种情形。

由式(1)、(4)及(11)知

再由式(5), (7), (9), (14), (15)知, 方程(1)的解一致持久。

2 应用

举例说明之前的结论。

例1 对于基于比率的非自治的捕食者-食饵模型

具有一致持久性。

[1] Li H, She Z. Uniqueness of periodic solutions of a nonautonomous density-dependent predator-prey system [J]. Math Anal Appl, 2015, 422: 886-905.

[2] She Z, Li H. Dynamics of a density-dependent stage-structured predator–prey system with Beddington–DeAngelis functional response [J]. Math Anal Appl, 2013, 406: 188–202.

[3] Kratina P, Vos M, Bateman A, et al. Functional response modified by predator density [J]. Oecologia, 2009, 159: 425-433.

[4] Arditi R, Ginzburg L R. Coupling in Predator-Prey Dynamics: Ratio-Dependence [J]. Journal of Theoretical Biology, 1989, 139: 311-326.

[5] Freedman H I, Wu J H. periodic solutions of single-species models with periodic delay [J]. SIAM J Math Anal, 1992, 23: 689-701.

[6] Nefedov N N, Recke L, Schneider K R. existence and asymptotic stability of periodic solutions with an interior layer of reactin-advection-diffusion equations [J]. Math Anal Appl, 2013, 405: 90-103.

[7] Wang Z, Wu J. Qualitative analysis for a ratio-dependent predator-prey model with stage-structure and diffusion [J]. Nonlinear Anal Real world appl, 2008, 9: 2 270-2 287.

[8] Ko W, Ahn I. A diffusive one-prey and two-competing-predator system with a ratio-dependent functional response: I, long time behaviour and stability of equilibria [J]. Math Anal Appl, 2013, 397: 9-28.

[9] Fan Y H, W L L. Multiplicity of periodic solutions for a delayed ratio-dependent predator-prey model with monotonic functional response and harvesting terms [J]. Anal Math Comput, 2014, 244: 878-894.

[10] Ding X Q, Jiang J F. Periodicity in a generalized semi-ratio-dependent predator-prey system with time delays and impulses [J]. Math Anal Appl, 2009, 360(1): 223-234.

[11] Hale J K. Theory of Functional Differential Equations [M]. New York: Springer-Verlag, 1977.

(责任编校:刘晓霞)

The uniform persistence of a kind of nonautonomous density-dependent delay predator-prey system

Jiang Yan, Yang Xitao

(School of mathematics, Hunan university of science and technology, Xiangtan411201, China)

The dynamic behaviour for a class of nonautonomous density-dependent delay predator-prey system is studied. By using the comparison principle, some sufficient conditions that guarantee the uniform persistence of the model are determined.

predator-prey system; uniform persistence; density-dependent; delay

10.3969/j.issn.1672–6146.2017.01.003

O 175.1

A

1672–6146(2017)01–0009–04

蒋燕, 1610422935@qq.com。

2016-06-25

湖南省自然科学基金(2015JJ2063); 2016年湖南省研究生创新基金(CX2016B534)。