基于主元独立性分析与混合核RVM的复杂过程区间预测方法研究及应用

徐圆，张明卿



基于主元独立性分析与混合核RVM的复杂过程区间预测方法研究及应用

徐圆，张明卿

（北京化工大学信息科学与技术学院，北京100029）

近年来，随着化工过程日趋复杂，对过程监控及关键变量预测提出了更高的要求。传统意义上的点预测已不能满足化工过程上的实际需求，且点预测无法描述过程上的不确定性问题，因此不能很好地把握预测变量的趋势。由此，提出了一种基于主元独立性分析（principal component independent analysis, PCIA）与混合核相关向量机（RVM）的区间预测方法。首先，结合核主元成分分析（KPCA）和独立元分析（ICA）对复杂过程原始变量进行主元成分提取和独立性分析，形成独立主元；其次，将高斯核函数与多项式核函数相结合形成混合核，与RVM结合对得到的独立主元进行回归建模预测，并运用T分布对预测值进行区间估计；然后，构造区间评价综合函数对区间估计结果进行优劣分析，在分析预测区间覆盖率（PICP）及预测区间宽度（NMPIW）的基础上，引入累积偏差（AD）提高区间评判的合理性。最后，将所提方法应用到TE仿真过程进行区间预测分析，仿真结果表明，提出的区间预测方法对实际生产过程具有较高的预测精度和区间估计质量，可以有效地预测关键变量的趋势。

核主元分析；独立主元分析；相关向量机；预测模型；区间评价

引 言

当今，实际化工过程日趋复杂，对其过程监控以及关键变量预测有了更高的要求。传统意义上的点预测模型已不能很好地反映复杂过程关键变量的趋势，而区间预测不仅可以预测对象的不确定性，而且能增强对象的可靠性以及安全性。在预测过程中，区间预测指的是预测变量以某一概率落入某区间范围内，其不仅可以包含点预测，而且能预测出变量的整体趋势，预测效果较好。

目前，常见的区间预测的方法有两类：一类是利用点预测得到预测值后，根据数据特性分布或者比例系数法来构建区间。常见的预测方法有时间序列法[1-2]、贝叶斯[3]、MVE[4]、Bootstrap[5-7]、神经网络、支持向量机(SVM)等。时间序列法依据时间的顺序进行排列，在固定时间间隔下进行采样，通过拟合曲线和参数估计对所建立的模型进行描述[1-2]；Bootstrap方法基于重抽样方法，通过从原始数据中抽取多个bootstrap样本，从而对整体的分布进行统计[5-7]，但两种方法操作比较耗费时间。神经网络方法，以极限学习机为例[8-10]，研究者利用构造比例系数来获得区间，但区间估计结果依赖于优化过程，若优化局部收敛，会影响区间估计结果。支持向量机（SVM）[11-13]利用核函数将输入空间映射到高维空间，在高维空间里求解一个最优分类面，进而得到输入与输出之间的关系，但是核参数以及惩罚因子较难选择。有些学者还提出了基于最小二乘的SVM[14-15]，以及相关向量机（RVM）方法。另一类方法是直接得到预测区间，如神经网络上下限（LUBE）方法，通过构造多输入双输出的神经网络模型，直接得到预测区间的上下限，并将LUBE与智能优化算法结合，通过优化区间评价综合函数实现区间估计，但区间估计结果过分依赖于优化过程[16-23]。

针对以上问题，本文提出了一种基于主元独立性分析(principal component independent analysis, PCIA)与混合核相关向量机（RVM）的区间预测方法。核主元成分分析（KPCA）[24-25]方法可以针对复杂非线性问题进行降维以及解决数据变量相关性的问题，但是得到的主元之间容易存在耦合度较大的问题。KPCA本身虽然考虑了数据之间相关性的问题，但并未对其独立性进行分析。而ICA[26-27]虽然也能实现降维，并进行独立性分析，但并未考虑到变量之间本身相关性的问题。由此，本文将KPCA与ICA方法进行结合，对原始变量进行处理，不仅可以从数据中提取到主元成分，而且能进一步提取到互为独立的信息元，这样更能够从本质上描述过程的特征。

RVM[28-30]是SVM的一种改进方法，极大地减少了核函数的计算量，同时也克服了核函数必须满足Mercer的条件。大部分实际过程常选用高斯核函数作为RVM的核函数。高斯核函数属于典型的局部核函数，其具有较强的学习能力；而多项式核函数是全局核函数的典型代表，其具有很强的推广能力，因此，本文选取高斯核函数和多项式核函数结合的混合核函数用于RVM中。

考虑到实际工业过程数据方差2的估计值与真实值存在偏差，若仍利用正态分布构建区间会产生较大误差，而T分布不依附于方差的估计，构建的区间无须运用智能优化算法进行优化，减少了算法上的复杂性。同时，本文采用预测区间覆盖率（PICP）、预测区间宽度（NMPIW），并引入累积偏差（AD）构造区间评价综合函数，对区间估计结果进行综合评判。最后，运用TE过程进行仿真实验，实验结果表明本文所提的区间预测方法，区间模型预测精度较高，区间评价指标较好。

1 基于PCIA与混合核RVM的预测模型

1.1 PCIA

将输入数据（1,2,…,x∈R）映射到高维空间中。在空间内进行主元分析，对应的协方差矩阵是

假设特征值为，特征向量为

v=(2)

那么所有满足≠0的特征向量为

将式（1）和式（3）代入式（2）中，得到

〈,〉= 〈,v〉

=(x)=1,2,…,(4)

引入核函数：采用径向基核函数。

求解特征值和特征向量，式（4）转化为

n==[1,2,…,]T(5)

在对数据进行主元分析之前，对数据进行标准化处理得到

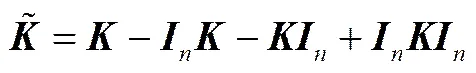
式（6）中为系数为1/与×的单位阵相乘。所以，求解特征值就等价于在状态空间中进行主元提取。求解特征向量时，需要满足

〈,〉=1,=1,2,…,(7)

为主元个数。

在此基础上计算样本在空间上的映射为

()为的第个主元分量。主元数量选择依照贡献率大于等于0.85的原则。然后对经过KPCA处理的主元分量，构建ICA模型，()T=,=-1()T，为独立元矩阵，为变换阵，引入分离矩阵，使得=-1()T=T，利用微分熵准则获得估计矩阵，从而推出独立元的估计。

1.2 混合核相关向量机（RVM）模型

对于给定的样本集(x,t)(=1,…,)，为样本数，则RVM定义的输出为

其中(,x)是核函数，本文采用混合核函数，选择要求

=0.1 (10)

w为权重，服从均值为零、方差为2的高斯分布，样本的极大似然函数定义为

其中

=(1,2,…,t)T;=(1,2,…,w)T;

()=((1),(2),…,(x))T;(x)=(1,(1,x),…,(x,x))T

由贝叶斯理论可得，条件概率为

其中，(·)为条件概率分布函数；(·)为条件概率密度函数。超参数=[1,2,…,]T，使得

(13)

因此，式（12）可改写为

对式（14）整理，得到后验分布概率密度为

(15)

式中，=(-2T+a)-1，=diag(1,2,…,)，=-2T。

采用极大似然得到和2的估计值。假设给定的输入值为*，且(|,,2|)满足高斯分布，其中输出为

*=(*)(16)

1.3 验证实验

为验证基于PCIA的混合核RVM的有效性，本文选取UCI数据集中Concrete Compressive Strength数据进行实证，采集800个数据样本进行实验，其中选取600个数据作为训练数据，200个数据作为测试数据，以模型测试的均方根误差RMSE、平均相对误差MAPE以及提取到的元数量（NE）作为评判验证指标。为表明PCIA的优势，将PCIA与KPCA、ICA进行比较（采用混合核RVM预测），结果如表1所示。

通过表1的比较结果可以看出，本文提出的PCIA方法在预测精度上明显优于其他方法。

表1 降维处理性能指标对比

2 T分布区间构建以及区间评价指标

2.1 T分布区间构建

对于样本(x,t)，预测输出y。t为样本真实值；定义误差=t-y，如果得到的满足(0,2)的分布，且每个元素都相互独立，那么满足

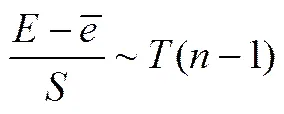
此时，依照参数的区间估计可以得到，当给定置信度为1-（这里取=0.1）时

(||≤/2)=1-(18)

构建区间形式为

2.2 预测区间评价指标

本文采用预测区间覆盖率（PICP），预测区间宽度（NMPIW），以及在两者基础上引入累积偏差（AD）提高区间评判的合理性。

（1）预测区间覆盖率（PICP）

表示真实值落在预测区间内的概率。值越大，说明预测区间效果越好。

(21)

式中，(X)、(X)分别为第时刻预测区间的上下限。

（2）预测区间宽度（NMPIW）

将MPIW标准化，得到

NMPIW=MPIW/(23)

式中，=max(Real)-min(Real)。

（3）构造预测区间宽度范围综合评价函数（PICWC）

上述两个指标互相独立，只考虑了区间评价的某一特征，由此，构造预测区间宽度范围综合评价函数（PICWC），以综合考虑PICP与NMPIW两者的共同影响作用。

PICWC=NMPIW×(1+(PICP)×e-(PICP-)) (24)

其中

进行必要的简化和一定的夸张，在写实的形象中寻找内在结构的抽象意味。使他的作品更加贴近生活。在进行创作时，不能丢弃传统，他需要传统的绘画精神作为支撑，需要对民族的各个方面进行了解才能使少数民族题材的工笔人物在真正意义上得到创新和发展。

式中，和都是常数，=1-(a取0.1)。根据实践经验取50。当PICP小于时，PICWC将迅速变大，导致预测区间不可行。当PICP大于时，指数项的作用将减小，甚至可以忽略，得到PICWC＝NMPIW，由此不会受到指数项的干扰而影响预测区间。

（4）引入累积偏差（AD）

考虑到预测区间覆盖的真实值偏离预测上限（或下限）的程度不同，要求真实值应尽量均匀分布在区间之中。观察图1与图2发现，图1的偏离程度明显高于图2，因此图2构建的区间预测要优于图1。但若仅用式（24）的综合评价函数进行评价，如上两个区间将被看作等效区间，并不能对其二者做出判断。

针对这一问题，引入累积偏差（AD）指标

(25)

式中，为预测值偏离预测区间的程度，该值越小越好。

3 实验及结果分析

本文采用TE过程进行仿真实验，验证所提方法的有效性。TE过程是一个经典的化工过程，主要包含反应器、压缩机、冷凝器、解析塔和分离器5个部分，含有41个测量变量和12个操作变量。实验过程：运行TE仿真模型，时间设置为24 h，得到仿真数据，选取其中反应器温度作为目标变量。取仿真过程中2200个数据作为训练数据，选取200个数据作为测试数据。首先，运用双变量相关分析得出与目标变量显著相关的多变量；其次，将得到的多变量利用PCIA进行降维与独立性分析；然后，将独立元利用混合核RVM进行回归预测，构建T分布区间，并计算PICP，NMPIW，PICWC与AD指标。为了表明所提出方法的有效性，与基于PCIA 的RVM方法、混合核RVM方法、RVM、SVM方法进行比较，测试过程如图3～图7所示。

为了进一步对比区间预测效果，本文还与BP以及正态分布构建方法进行对比。测试过程如图8、图9所示。

上述7种方法区间预测性能指标结果如表2所示。

表2 区间预测性能指标对比

从图3～图6可以看出，本文提出的区间预测方法能够有效地包含真实值，其上下波动趋势与实际真实值基本一致，通过表2各种评价指标结果可以得出，所提方法区间宽度最窄，综合作用效果最好，与PCIA-RVM、混合核RVM、RVM相比，平均区间宽度、累积偏差都得到了改善；由图7、图8可以看出基于SVM以及基于PCIA-BP这两种方法不能很好地包含真实值，不能很好地反映预测趋势，而且通过表2也可以看出两种方法区间覆盖率太低，故其他区间指标不做计算；由图9可以看出基于正态分布的PCIA-混合核RVM预测区间方法大体上能够覆盖真实值，但存在部分真实值散落在预测区间之外，且区间覆盖、平均宽度以及累计偏差均比本文所提方法差。综上所述，基于PCIA与混合核RVM的区间预测方法可以很好地实现复杂过程变量区间预测，并描述关键变量的变化趋势。

4 结 论

针对复杂工业过程要求在早期就能预测出问题的这一发展趋势，区间预测不仅可以包含点预测的优点，而且还可以较好地描述出问题的不确定性与趋势。本文提出了一种基于PCIA与混合核RVM的预测模型，通过回归预测、T分布区间构造并进行区间估计综合评价，并将此方法应用到TE过程进行区间预测仿真。通过与几种常用方法的对比以及结果分析，可以看出本文提出的方法不仅预测精度和区间估计质量上有明显的提高，而且能够较好地描述复杂过程变量变化趋势，较好地满足了实际复杂工业过程的应用要求。

References

[1] FARUK D O. A hybrid neural network and ARIMA model for water quality time series prediction[J]. Engineering Applications of Artificial Intelligence, 2010, 23(4): 586-594.

[2] XIONG T, BAO Y, HU Z,. Forecasting interval time series using a fully complex-valued RBF neural network with DPSO and PSO algorithms[J]. Information Sciences, 2015, 305: 77-92.

[3] KHOSRAVI A, MAZLOUMIE, NAHAVANDI S,Prediction intervals to account for uncertainties in travel time prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(2): 537-547.

[4] NIX DA, WEIGEMD A S. Estimating the mean and variance of the target probability distribution[C]// IEEE World Congress on IEEE International Conference on Neural Networks. 1994: 55-60

[5] LI P, DIMITRIS N. Bootstrap prediction intervals for linear, nonlinear and nonparametric autoregressions[J]. Journal of Statistical Planning and Inference, 2014, 177: 1-27.

[6] TRUCIOS C, HOTTA L K. Bootstrap prediction in univariate volatility models with leverage effect[J]. Mathematics and Computers in Simulation, 2016, 120:91-103.

[7] 党宏涛, 杜祖良, 任宏文, 等. 基于Bootstrap方法的平台惯导系统标定参数重复性区间预测[J]. 中国惯性技术学报, 2013, 21(3): 411-414. DANG H T, DU Z L, REN H W,. Repeatability interval prediction for calibrated parameters of INS based on Bootstrap method[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 411-414.

[8] WANG C, NIU M, SONG Y H,Pareto optimal prediction intervals of electricity price[J]. IEEE Transactions on Power Systems, 2016, 32: 1.

[9] 李知艺, 丁剑鹰, 吴迪, 等. 电力负荷区间预测的集成极限学习机方法[J]. 华北电力大学学报, 2014, 41(2): 78-88. LI Z Y, DING J Y, WU D,An ensemble model of the extreme learning machine for load interval prediction[J]. Journal of North China Electric Power University, 2014, 41(2): 78-88.

[10] WAN C, XU Z, PINSON P,. Probabilistic forecasting of wind power generation using extreme learning machine[J]. IEEE Transactions on Power Systems, 2014, 29(29): 1033-1044.

[11] VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 1995: 52-123.

[12] SHRIVASTAVA N A, KHOSRAVI A, PANIGRAHI B K. Prediction interval estimation of electricity prices using PSO-tuned support vector machines[J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 322-331.

[13] ZHAO J H, DONG Z Y, XU Z,. A statistical approach for interval forecasting of the electricity price[J]. IEEE Transactions on Power Systems, 2008, 23(2): 267-276.

[14] DE B K, DE B J, SUYKENS J A. Approximate confidence and prediction intervals for least squares support vector regression[J]. IEEE Transactions on Neural Networks, 2010, 22(1): 110-120.

[15] CHENG Q, TEZCAN J, CHENG J. Confidence and prediction intervals for semiparametric mixed-effect least squares support vector machine[J]. Pattern Recognition Letters, 2014, 40(40): 88-95.

[16] KHOSRAVI A, NAHAVANDI S, CREIGHTON D,Lower upper bound estimation method for construction of neural network-based prediction intervals[J]. IEEE Transactions on Neural Networks, 2011, 22(3): 337-46.

[17] HAO Q, SRINIVASAN D, KHOSRAVI A. Uncertainty handling using neural network-based prediction intervals for electrical load forecasting[J]. Energy, 2014, 73(7): 916-925.

[18] ZHANG G, WU Y, WONG K P,. An advanced approach for constructionof optimal wind power prediction intervals[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2706-2715.

[19] HAO Q, SRINIVASAN D, KHOSRAVI A. Short-Term load and wind power forecasting using neural network-based prediction intervals[J]. IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(2): 303-315.

[20] KAVOUSI-FARD A, KHOSRAVI A, NAHAVANDI S. A New fuzzy-based combined prediction intervalfor wind power forecasting[J]. IEEE Transactions on Power Systems, 2015, 31(1): 1-9.

[21] WAN C, XU Z, PINSON P,. Optimal prediction intervals of wind power generation[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1166-1174.

[22] HOSEN M, KHOSRAVI A, NAHAVANDI S,Prediction interval-based neural network modelling of polystyrene polymerization reactor—a new perspective of data-based modelling[J]. Chemical Engineering Research & Design, 2014, 92(11): 2041-2051.

[23] 韩帅, 李树刚. 基于区间预测模型的流感趋势预测[J]. 计算机仿真, 2014, 31(9): 237-242. HAN S, LI S G. Influenza trends forecast based on interval prediction model[J]. Computer Simulation, 2014, 31(9): 237-242.

[24] SCHLKOPF B, SMOLA A, MULLER K. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319.

[25] 李海波, 柴天佑, 岳恒. 浮选工艺指标KPCA-ELM软测量模型及应用[J]. 化工学报, 2012, 63(9): 2892-2898. LI H B, CHAI T Y, YUE H. Soft sensor of technical indices based on KPCA-ELM and application for flotation process[J]. CIESC Journal, 2012, 63(9): 2892-2898.

[26] STEFATOS G, HAMZA A B. Dynamic independent component analysis approach for fault detection and diagnosis[J]. Expert Systems with Applications, 2010, 37(12): 8606-8617.

[27] KANO M, HASEBE S, HASHIMOTO I,. Evolution of multivariate statistical process control: application of independent component analysis and external analysis[J]. Computers and Chemical Engineering, 2004, 28(6/7): 1157-1166.

[28] MIANJI F A, ZHANG Y. Robust hyperspectral classification using relevance vector machine[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(6): 2100-2112.

[29] TIPPING M. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244.

[30] 杨树仁, 沈洪远. 基于相关向量机的机器学习算法研究与应用[J]. 计算技术与自动化, 2010, 29(1): 43-47. YANG S R, SHEN H Y. Research and application of machine learning algorithm based on relevance vector machine[J]. Computing Technology and Automation, 2010, 29(1): 43-47.

Research and application of interval prediction method for complex processes based on principal component independent analysis and mixed kernel RVM

XU Yuan, ZHANG Mingqing

(School of Information Science & Technology, Beijing University of Chemical Technology, Beijing100029, China)

In recent years, higher requirements have been put forward to process monitoring and key variable prediction with increasing complexity of chemical processes. Traditional point predictions do not meet these actual needs nor describe uncertainty concern, so that they could not predict variable trending well. An interval prediction method was proposed from principal component independent analysis and mixed kernel RVM. First, kernel principal component analysis (KPCA) and independent element analysis (ICA) were combined to extract principal components from original variables in complex process and to form independent principal components by independent analysis. Second, mixed kernel from Gauss and polynomial kernel functions and RVM were combined to generate a regression prediction model for the independent principal components, and T distribution was used to make interval estimation on predicted values of the model. Third, comprehensive interval evaluation function was constructed to analyze quality of the interval estimation results. Based on prediction interval coverage probability (PICP) and normal mean prediction interval width (NMPIW), accumulative deviation (AD) was introduced to improve rationality of the interval evaluation. The interval prediction analysis on TE simulation process showed that the proposed interval prediction method had better prediction accuracy and interval estimation quality, which could effectively predict trending of key variables in actual production process.

kernelprincipal component analysis; independent component analysis; relevance vector machine; prediction model; interval evaluation

10.11949/j.issn.0438-1157.20161559

TP 29

A

0438—1157（2017）03—0925—07

国家自然科学基金项目(61573051，61472021)；软件开发环境国家重点实验室开放课题(SKLSDE-2015KF-01)；中央高校基本科研业务费专项资金项目(PT1613-05)。

2016-11-04收到初稿，2016-11-08收到修改稿。

联系人及第一作者：徐圆（1983—），女，博士，副教授。

2016-11-04.

XU Yuan, associate professor, xuyuan@mail. buct.edu.cn

supported by the National Natural Science Foundation of China (61573051,61472021), the Open Fund of the State Key Laboratory of Software Development Environment (SKLSDE-2015KF-01) and the Fundamental Research Funds for Central Universities ofChina (PT1613-05)